Giải SBT toán hình học và đại số 10 nâng cao Bài 1. Giá trị lượng giác của một góc bất kì (Từ 0 độ đ..

Bài 3 trang 38 SBT Hình học 10 Nâng cao


Giải bài tập Bài 3 trang 38 SBT Hình học 10 Nâng cao

Đề bài

a)  Chứng minh rằng \({\sin ^2}x + {\cos ^2}x = 1\,\,({0^0} \le x \le {180^0}).\)

b) Tìm \(\sin x\) khi \(\cos x =  - \dfrac{1}{3}.\)

c) Tìm \(\cos x\) khi \(\sin x=0,3.\)

c) Tìm \(\cos x\) và \(\sin x\) khi \(\sin x - \cos x = \dfrac{2}{3}.\)

Lời giải chi tiết

(h.26).

 

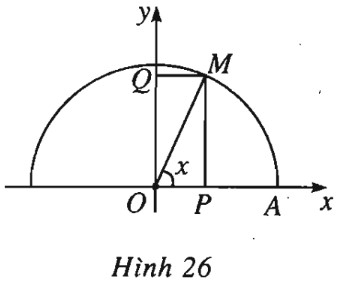
a) \(\sin x = \overline {OQ}, \cos x = \overline {OP},\)

\({\sin ^2}x + {\cos ^2}x = O{Q^2} + O{P^2} = 1.\)

b) \(\sin x = \sqrt {1 - {{\cos }^2}x}  = \dfrac{{2\sqrt 2 }}{3}.\)

c) \(\cos x =  \pm \sqrt {1 - {{\sin }^2}x}  =  \pm \sqrt {0,91} .\)

d) Giải hệ \(\left\{ \begin{array}{l}\sin x - \cos x = \dfrac{2}{3}\\{\sin ^2}x + {\cos ^2}x = 1\end{array} \right.\)

Ta có \(\sin x = \dfrac{{\sqrt {14}  + 2}}{6}, \cos x = \dfrac{{\sqrt {14}  - 2}}{6}.\)

Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store