Giải bài 3.37 trang 50 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
Trong hình 3.37 có
Đề bài
Trong hình 3.37 có \(BE// AC,CF// AB\). Biết \(\widehat A = {80^0};\widehat {ABC} = {60^0}\).
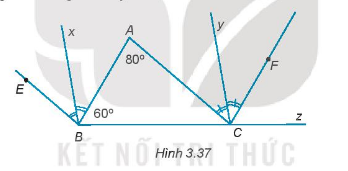
a) Chứng minh rằng \(\widehat {ABE} = \widehat {ACF}.\)
b) Tính số đo của các góc BCF và ACB.
c) Gọi Bx, Cy lần lượt là tia phân giác của các góc ABE và ACF. Chứng minh rằng \(Bx// Cy\).
Phương pháp giải - Xem chi tiết
a) Chứng minh 2 góc ABE và ACF cùng bằng góc A.
b)
- Tính góc FCz (chỉ ra cặp góc đồng vị).
- Tính góc BCF (Kề bù với góc FCz)
c)
- Tính \(\widehat{ABx}, \widehat{FCy}\).
- Chứng minh \(\widehat{xBC}= \widehat{yCz}\).
Lời giải chi tiết
a) Vì \(BE// AC \) nên \( \widehat {ABE} = \widehat A\) (cặp góc so le trong).
Mà \(\widehat A= {80^0}\) nên \(\widehat {ABE} =80^0\)
Vì \(AB//CF\) nên \( \widehat {ACF} = \widehat A \) (cặp góc so le trong).
Mà \(\widehat A= {80^0}\) nên \(\widehat {ACF} =80^0\)
Suy ra \(\widehat {ABE} = \widehat {ACF}.\)
b) Vì \(AB// FC \) nên \( \widehat {zCF} = \widehat {CBA}\) (cặp góc đồng vị).
Mà \(\widehat {CBA}= {60^0}\) nên \(\widehat {zCF} =60^0\)
Lại có: \(\widehat {zCF} + \widehat {BCF} = {180^0}\) (2 góc kề bù)
\(\begin{array}{l} {60^0} + \widehat {BCF} = {180^0}\\ \text{suy ra }\widehat {BCF} = {180^0} - {60^0}= {120^0}\end{array}\)
Tia AC nằm trong góc BCF nên \(\widehat {ACB} = \widehat {BCF} - \widehat {ACF} = {120^0} - {80^0} = {40^0}\).
c) Ta có: \(\widehat {EBx} = \widehat {xBA} = \widehat {ACy} = \widehat {yCF} = {40^0}\)
Nên \(\widehat {xBC} = \widehat {xBA} + \widehat {ABC} = {40^0} + {60^0} = {100^0}\)
\(\widehat {yCz} = \widehat {yCF} + \widehat {FCz} = {40^0} + {60^0} = {100^0}\)
Suy ra \( \widehat {xBC} = \widehat {yCz}\left( { = {{100}^0}} \right)\)
Mà 2 góc ở vị trí đồng vị nên \(Bx// Cy\) (Dấu hiệu nhận biết hai đường thẳng song song)
- Giải bài 3.36 trang 50 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
- Giải bài 3.35 trang 49 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
- Giải bài 3.34 trang 49 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
- Giải bài 3.33 trang 49 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
- Giải Câu hỏi trắc nghiệm trang 47,48 sách bài tập Toán 7 Kết nối tri thức với cuộc sống
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 7 - Kết nối tri thức - Xem ngay
Các bài khác cùng chuyên mục
- Giải Bài 18 trang 71 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
- Giải Bài 17 trang 71 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
- Giải Bài 16 trang 71 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
- Giải Bài 15 trang 71 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
- Giải Bài 14 trang 70 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
- Giải Bài 18 trang 71 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
- Giải Bài 17 trang 71 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
- Giải Bài 16 trang 71 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
- Giải Bài 15 trang 71 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
- Giải Bài 14 trang 70 sách bài tập toán 7 - Kết nối tri thức với cuộc sống













Danh sách bình luận