Bài 10: Tiên đề Euclid. Tính chất của hai đường thẳng s..

Giải bài 3.19 trang 42 sách bài tập toán 7 - Kết nối tri thức với cuộc sống


Vẽ lại hình 3.20 vào vở.

Đề bài

Vẽ lại hình 3.20 vào vở.

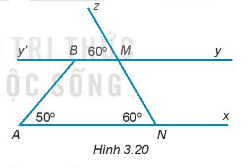
a) Giải thích tại sao \(Ax\parallel By.\)

b) Tính số đo góc \(ABy'\).

c) Tính số đo góc ABM.

Phương pháp giải - Xem chi tiết

a) Chỉ ra 2 góc đồng vị bằng nhau

b) Chỉ ra 2 góc so le trong bằng nhau

c) \(\widehat {ABM} + \widehat {ABy'} = {180^0}\) 

Lời giải chi tiết

a)

Ta có: \(\widehat {BMz} = \widehat {ANM}\left( { = {{60}^0}} \right)\)

Mà hai góc ở vị trí đồng vị nên \(Ax\parallel By\)(dấu hiệu nhận biết 2 đường thẳng song song).

b)

Ta có: \(Ax\parallel By\)\( \Rightarrow \widehat {ABy'} = \widehat {BAN}\)(2 góc so le trong)

Do đó \(\widehat {ABy'} = {50^0}\).

c)

Ta có: \(\widehat {ABM} + \widehat {ABy'} = {180^0}\) (hai góc kề bù)

\(\begin{array}{l} \Rightarrow \widehat {ABM} + {50^0} = {180^0}\\ \Rightarrow \widehat {ABM} = {180^0} - {50^0}\\ \Rightarrow \widehat {ABM} = {130^0}\end{array}\) 


Bình chọn:
4.6 trên 18 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 7 - Kết nối tri thức - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store