-
SBT TOÁN TẬP 1 - KẾT NỐI TRI THỨC VỚI CUỘC SỐNG
-
SBT TOÁN TẬP 2 - KẾT NỐI TRI THỨC VỚI CUỘC SỐNG
Giải bài 3 trang 70 sách bài tập toán 10 - Kết nối tri thức với cuộc sống
Cho tam thức bậc hai với đồ thị là parabol có đỉnh I(1, 4) và đi qua điểm A(2; 3) a) Xác định các hệ số a, b, c của tam thức bậc hai f(x).
Đề bài
Cho tam thức bậc hai với đồ thị là parabol có đỉnh I(1; 4) và đi qua điểm A(2; 3).
a) Xác định các hệ số a, b, c của tam thức bậc hai f(x).
b) Vẽ parabol này.
c) Từ đồ thị đã vẽ ở câu b), hãy cho biết khoảng đồng biến, khoảng nghịch biến và tập giá trị của hàm số y = f(x).
d) Lập bảng xét dấu để giải bất phương trình \(\frac{{f(x)}}{{x - 2}} \ge 0\).
Lời giải chi tiết
a) Parabol có đỉnh là I(1; 4) nên phương trình có dạng \(y = a{(x - 1)^2} + 4\).
Vì điểm A(2; 3) thuộc parabol nên ta có:
\(3 = a{(2 - 1)^2} + 4 \Rightarrow a = - 1\).
Vậy tam thức cần tìm là \(f(x) = - {x^2} + 2x + 3\) ta có a = -1, b = 2, c = 3.
b) Ta có a = -1.
Đỉnh I(1; 4), trục đối xứng x = 1.
Giao điểm của parabol với trục Oy là (0; 3), với trục Ox là (-1; 0) và (3; 0).
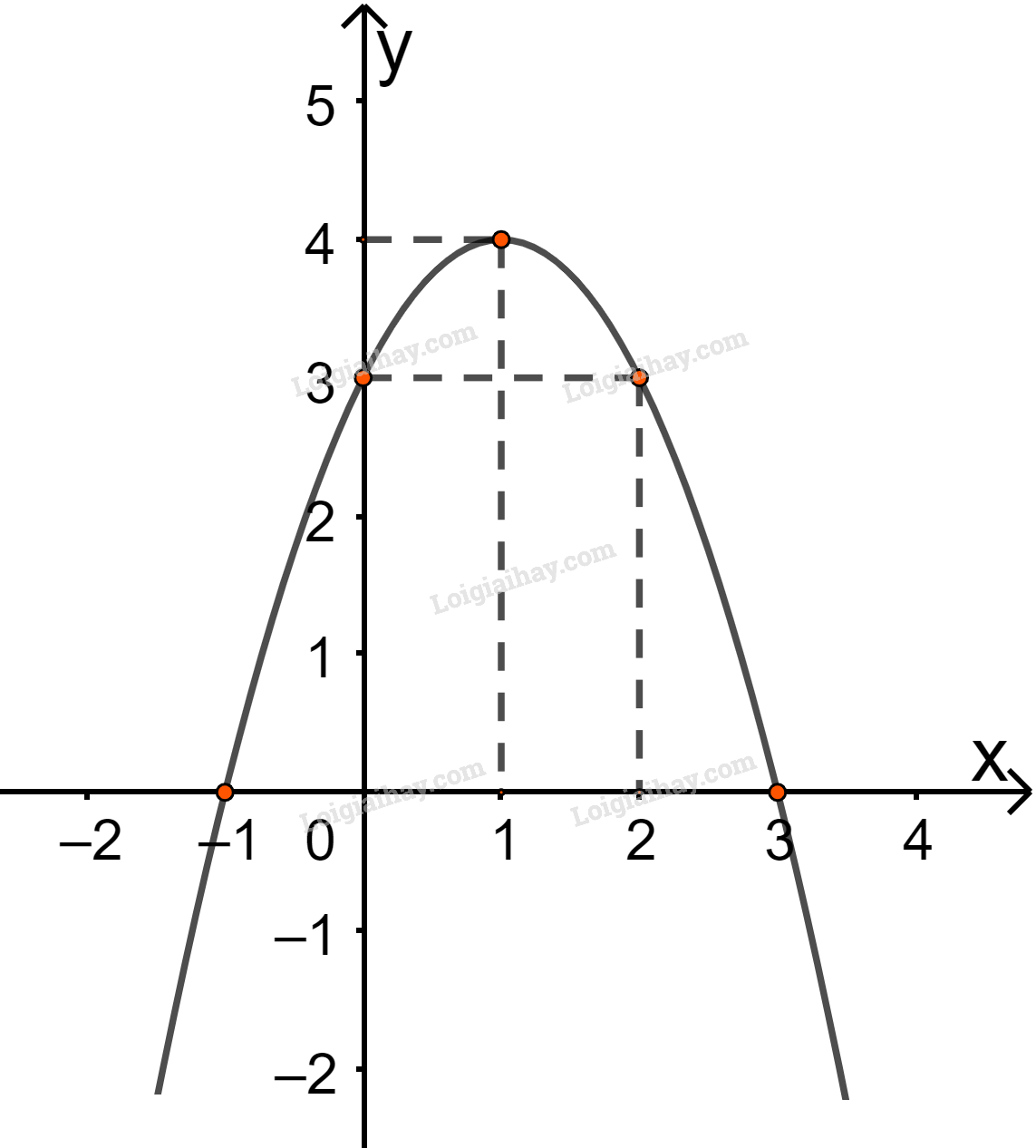
c) Hàm số đồng biến trên khoảng (-∞; 1), nghịch biến trên khoảng (1; +∞).
Tập giá trị của hàm số là (-∞; 4].
d) Xét bất phương trình \(\frac{{f(x)}}{{x - 2}} \ge 0\) hay \(\frac{{ - {x^2} + 2x + 3}}{{x - 2}} \ge 0\).
\(f(x) = - {x^2} + 2x + 3 = 0 \Leftrightarrow x = - 1\) hoặc \(x = 3\).
\(x - 2 = 0 \Leftrightarrow x = 2\).
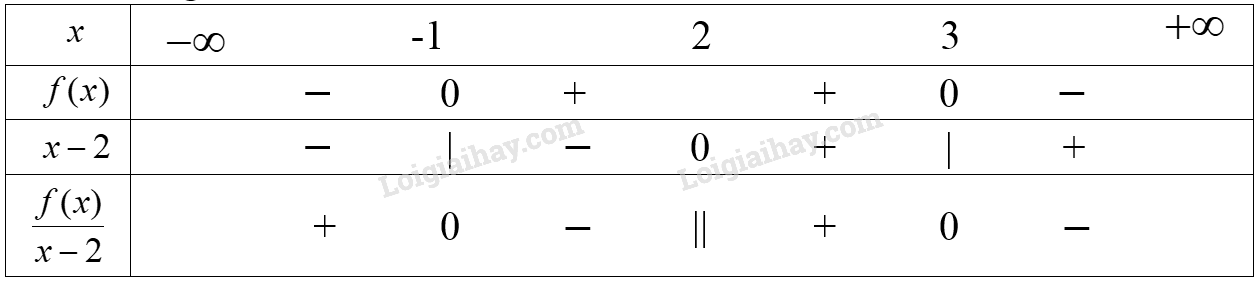
Ta có bảng xét dấu sau:
Vậy tập nghiệm của bất phương trình đã cho là \(( - \infty ; - 1] \cup (2;3]\).
Bình luận
Chia sẻ
- Giải bài 4 trang 71 sách bài tập toán 10 - Kết nối tri thức với cuộc sống
- Giải bài 5 trang 71 sách bài tập toán 10 - Kết nối tri thức với cuộc sống
- Giải bài 6 trang 71 sách bài tập toán 10 - Kết nối tri thức với cuộc sống
- Giải bài 7 trang 72 sách bài tập toán 10 - Kết nối tri thức với cuộc sống
- Giải bài 8 trang 72 sách bài tập toán 10 - Kết nối tri thức với cuộc sống
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Kết nối tri thức - Xem ngay
PH/HS Tham Gia Nhóm Lớp 10 Để Trao Đổi Tài Liệu, Học Tập Miễn Phí!
