-
ĐẠI SỐ VÀ GIẢI TÍCH - TOÁN 11 NÂNG CAO
-
HÌNH HỌC- TOÁN 11 NÂNG CAO
Giải toán 11, giải bài tập toán 11 nâng cao, Toán 11 Nâng cao, đầy đủ đại số giải tích và hình học
Câu hỏi trắc nghiệm ôn tập chương II
Câu 8 trang 80 SGK Hình học 11 Nâng cao
Cho tứ diện đều ABCD có cạnh bằng a. Gọi G là tọng tâm tam giác ABC. Cắt tứ diện bởi mp(GCD) thì diện tích của thiết diện là :
Đề bài
Cho tứ diện đều ABCD có cạnh bằng a. Gọi G là tọng tâm tam giác ABC. Cắt tứ diện bởi mp(GCD) thì diện tích của thiết diện là :
A. \({{{a^2}\sqrt 3 } \over 2}\)
B. \({{{a^2}\sqrt 2 } \over 4}\)
C. \({{{a^2}\sqrt 2 } \over 6}\)
D. \({{{a^2}\sqrt 3 } \over 4}\)
Lời giải chi tiết
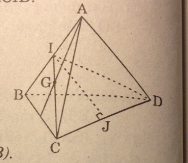
Gọi I là trung điểm của AB. Thiết diện cần tìm là ΔCID
Gọi J là trung điểm CD
ΔCID cân nên IJ ⊥ CD ⇒ \({S_{ICD}} = {1 \over 2}IJ.CD\)
Ta có:
\(\eqalign{ & I{J^2} = C{I^2} - C{J^2} = {\left( {{{a\sqrt 3 } \over 2}} \right)^2} - {{{a^2}} \over 4} = {{{a^2}} \over 2} \cr & \Rightarrow IJ = {{a\sqrt 2 } \over 2} \Rightarrow {S_{ICD}} = {1 \over 2}.{{a\sqrt 2 } \over 2}.a = {{{a^2}\sqrt 2 } \over 4} \cr} \)
Chọn (B)
Loigiaihay.com
Bình luận
Chia sẻ
- Câu 9 trang 80 SGK Hình học 11 Nâng cao
- Câu 10 trang 80 SGK Hình học 11 Nâng cao
- Câu 11 trang 80 SGK Hình học 11 Nâng cao
- Câu 12 trang 80 SGK Hình học 11 Nâng cao
- Câu 7 trang 79 SGK Hình học 11 Nâng cao
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
