Giải toán 11, giải bài tập toán 11 nâng cao, Toán 11 Nâng cao, đầy đủ đại số giải tích và hình học Bài 6. Phép vị tự

Câu 29 trang 29 SGK Hình học 11 Nâng cao


Đề bài

Cho đường tròn (O; R) và điểm I cố định khác O. Một điểm M thay đổi trên đường tròn. Tia phân giác của góc MOI cắt IM tại N. Tìm quỹ tích điểm N

Lời giải chi tiết

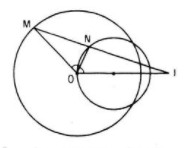
Đặt \(IO = d (d ≠ 0)\). Theo tính chất đường phân

giác của tam giác MOI, ta có:

\({{IN} \over {NM}} = {{IO} \over {OM}} = {d \over R}\)

Suy ra \({{IN} \over {IN + NM}} = {d \over {d + R}} \Leftrightarrow {{IN} \over {IM}} = {d \over {d + R}}\)

Vì hai vecto \(\overrightarrow {IN} \) và \(\overrightarrow {IM} \) cùng hướng nên đẳng

thức trên có nghĩa là:\(\overrightarrow {IN} = {d \over {d + R}}\overrightarrow {IM} \)

Nếu gọi V là phép vị tự tâm I tỉ số \(k = {d \over {d + R}}\) thì V biến điểm M thành điểm N

Khi M ở vị trí M0trên đường tròn (O ; R) sao cho \(\widehat {IO{M_0}} = {0^ \circ }\) thì tia phân giác của góc \(\widehat {IO{M_0}}\) không cắt IM. Điểm N không tồn tại.

Vậy khi M chạy trên (O ; R) (M khác hẳn M0) thì quỹ tích điểm N là ảnh của (O ; R) qua phép vị tự V bỏ đi ảnh của điểm M0

Loigiaihay.com


Bình chọn:
3.7 trên 6 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay

Báo lỗi - Góp ý

>> Luyện thi TN THPT & ĐH năm 2023 trên trang trực tuyến Tuyensinh247.com. Học mọi lúc, mọi nơi với Thầy Cô giáo giỏi, đầy đủ các khoá: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng; Tổng ôn chọn lọc.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua