-
ĐẠI SỐ VÀ GIẢI TÍCH - TOÁN 11 NÂNG CAO
-
HÌNH HỌC- TOÁN 11 NÂNG CAO
Giải toán 11, giải bài tập toán 11 nâng cao, Toán 11 Nâng cao, đầy đủ đại số giải tích và hình học
Bài 5. Hai hình bằng nhau
Câu 23 trang 23 SGK Hình học 11 Nâng cao
Hình gồm ba đường tròn
Đề bài
Hình H1 gồm ba đường tròn \(\left( {{O_1};{r_1}} \right),\left( {{O_2};{r_2}} \right)\) và \(\left( {{O_3};{r_3}} \right)\) đôi một tiếp xúc ngoài với nhau. Hình H2 gồm ba đường tròn \(\left( {{I_1};{r_1}} \right),\left( {{I_2};{r_2}} \right)\) và \(\left( {{I_3};{r_3}} \right)\) đôi một tiếp xúc ngoài với nhau. Chứng tỏ rằng hai hình H1 và H2 bằng nhau.
Lời giải chi tiết
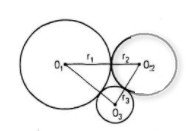
Ta có
\({{O_1}{O_2} = {r_1} + {\rm{ }}{r_2} = {I_1}{I_2}}\)
\({{O_2}{O_3} = {r_2} + {\rm{ }}{r_3} = {I_2}{I_3}} \)
\({{O_3}{O_1} = {r_3} + {\rm{ }}{r_1} = {I_3}{I_1}} \)
Suy ra \(\Delta {O_1}{O_2}{O_3} = \Delta {I_1}{I_2}{I_3}\) nên có phép dời hình F biến ba điểm O1, O2, O3 lần lượt thành ba điểm I1, I2, I3
Hiển nhiên khi đó F biến ba đường tròn \(({O_{1}}{\rm{; }}{r_1}),{\rm{ }}({O_2};{\rm{ }}{r_2}),{\rm{ }}({O_3};{\rm{ }}{r_3})\) lần lượt thành ba đường tròn \(({I_1};{r_1}),({I_2};{r_2}),({I_3};{r_3})\), tức là biến hình H1 thành hình H2
Vậy hai hình H1 và H2 bằng nhau
Loigiaihay.com
Bình luận
Chia sẻ
Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
