Giải toán 10, giải bài tập Toán 10 Nâng cao, đầy đủ đại số giải tích và hình học

ÔN TẬP CUỐI NĂM HÌNH HỌC - TOÁN 10 NÂNG CAO

Bài 8 trang 128 SGK Hình học 10 nâng cao

Viết phương trình đường thẳng Δ đi qua M, N và tìm các giao điểm P, Q của Δ với hai đường tiệm cận của hypebol (H)

Lựa chọn câu để xem lời giải nhanh hơn

Cho hypebol (H) có phương trình \({{{x^2}} \over {16}} - {{{y^2}} \over 4} = 1\)

LG a

Viết phương trình các đường tiệm cận của hypebol (H).

Lời giải chi tiết:

Ta có: a² =16; b² = 4 => a= 4 và b = 2.

Phương trình các đường tiệm cận của hypebol (H) là

\(y = \pm {b \over a}x = \pm {1 \over 2}x\)

LG b

Tính diện tích hình chữ nhật cơ sở của hypebol (H).

Lời giải chi tiết:

Diện tích hình chữ nhật cơ sở của hypebol (H) là \(S = 4ab = 4.4.2 = 32\)

LG c

Chứng minh rằng các điểm \(M\left( {5\,;\,{3 \over 2}} \right)\,,\,N(8\,;\,2\sqrt 3 )\) đều thuộc (H).

Lời giải chi tiết:

Ta có \({{{5^2}} \over {16}} - {{{{\left( {{3 \over 2}} \right)}^2}} \over 4} = 1\) và \({{{8^2}} \over {16}} - {{{{\left( {2\sqrt 3 } \right)}^2}} \over 4} = 1\) nên M và N đều thuộc (H).

LG d

Viết phương trình đường thẳng Δ đi qua M, N và tìm các giao điểm P, Q của Δ với hai đường tiệm cận của hypebol (H).

Lời giải chi tiết:

Phương trình đường thẳng của MN

\(\Delta \,:\,\,{{x - 5} \over {8 - 5}} = {{y - {3 \over 2}} \over {2\sqrt 3 - {3 \over 2}}}\) \(\Leftrightarrow {{x - 5} \over 3} = {{2y - 3} \over {4\sqrt 3 - 3}}\)

Giao điểm P của Δ với tiệm cận \(y = {1 \over 2}x\) là nghiệm của hệ

\(\left\{ \matrix{
\,{{x - 5} \over 3} = {{2y - 3} \over {4\sqrt 3 - 3}} \hfill \cr
y = {1 \over 2}x \hfill \cr} \right.\) \(\Leftrightarrow \left\{ \matrix{
x = 8 + 2\sqrt 3 \hfill \cr
y = 4 + \sqrt 3 \hfill \cr} \right.\)

\(\Rightarrow \,\,P\,\left( {8 + 2\sqrt 3 \,;\,\,4 + \sqrt 3 } \right)\) .

Giao điểm Q của Δ với tiệm cận \(y = - {1 \over 2}x\) là nghiệm của hệ

\(\left\{ \matrix{
\,{{x - 5} \over 3} = {{2y - 3} \over {4\sqrt 3 - 3}} \hfill \cr
y = - {1 \over 2}x \hfill \cr} \right.\) \( \Leftrightarrow \,\,\,\left\{ \matrix{
x = 5 - 2\sqrt 3 \hfill \cr
y = - {5 \over 2} + \sqrt 3 \hfill \cr} \right. \)

\(\Rightarrow Q\left( {5 - 2\sqrt 3 \,;\, - {5 \over 2} + \sqrt 3 } \right)\)

Cách khác:

LG e

Chứng minh rằng các trung điểm của hai đoạn thẳng PQ và MN trùng nhau.

Lời giải chi tiết:

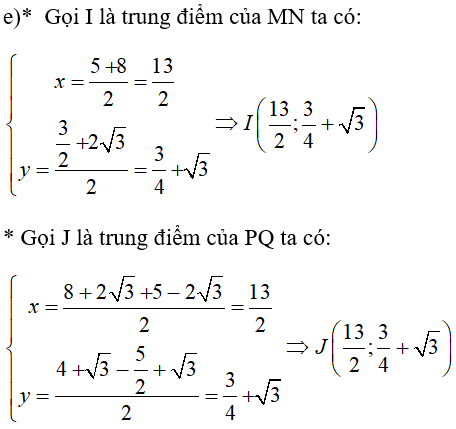
Vậy các trung điểm của hai đoạn thẳng PQ và MN trùng nhau.

Loigiaihay.com

👉

Giải bài nhanh với AI Hay:

Bình luận

Chia sẻ

Bình chọn:

3.3 trên 10 phiếu

Bài tiếp theo

Bài 9 trang 128 SGK Hình học 10 nâng cao
Xác định tọa độ tiêu điểm F và phương trình đường chuẩn d của (P)
Bài 7 trang 127 SGK Hình học 10 nâng cao
Tính khoảng cách từ gốc tọa độ O tới đường thẳng M1M2
Bài 6 trang 127 SGK Hình học 10 nâng cao
Viết phương trình đường phân giác trong tại đỉnh O của tam giác OAB
Bài 5 trang 127 SGK Hình học 10 nâng cao
Tìm liên hệ giữa để hai đường thẳng AB’ và A’B cắt nhau. Khi đó hãy tìm tọa độ giao điểm I của hai đường thẳng đó.
Bài 4 trang 127 SGK Hình học 10 nâng cao
Chứng minh rằng :
Bài 3 trang 127 SGK Hình học 10 nâng cao
Tính độ dài các đường trung tuyến và diện tích tam giác
Bài 2 trang 126 SGK Hình học 10 nâng cao
Cho tam giác vuông tại A, AB = c, AC = b . Gọi M là điểm trên cạnh BC sao cho CM = 2BM, N là điểm trên cạnh AB sao cho BN = 2AN (h.106).
Bài 1 trang 126 SGK Hình học 10 nâng cao
Chứng minh các đăng thức sau