 Giải toán 10, giải bài tập Toán 10 Nâng cao, đầy đủ đại số giải tích và hình học
Giải toán 10, giải bài tập Toán 10 Nâng cao, đầy đủ đại số giải tích và hình học
 ÔN TẬP CUỐI NĂM HÌNH HỌC - TOÁN 10 NÂNG CAO
ÔN TẬP CUỐI NĂM HÌNH HỌC - TOÁN 10 NÂNG CAO
Bài 7 trang 127 SGK Hình học 10 nâng cao
Tính khoảng cách từ gốc tọa độ O tới đường thẳng M1M2
Trong mặt phẳng tọa độ, với mỗi số \(m \ne 0\) , xét hai điểm \({M_1}( - 4\,;\,m);\,{M_2}(4\,;\,{{16} \over m})\)
LG a
Viết phương trình đường thẳng M1M2.
Lời giải chi tiết:
Ta có \(\overrightarrow {{M_1}{M_2}} = \left( {8\,;\,{{16} \over m} - m} \right) = \left( {8\,;\,{{16 - {m^2}} \over m}} \right)\)
\( \Rightarrow \overrightarrow n = \left( {\frac{{16 - {m^2}}}{m}; - 8} \right)\) là VTPT của đường thẳng \({M_1}{M_2}\).
Phương trình đường thẳng \({M_1}{M_2}\) đi qua \(M_1\) và nhận \(\overrightarrow n = \left( {\frac{{16 - {m^2}}}{m}; - 8} \right)\) làm VTPT là:
\(\begin{array}{l}
\frac{{16 - {m^2}}}{m}\left( {x + 4} \right) - 8\left( {y - m} \right) = 0\\
\Leftrightarrow \left( {16 - {m^2}} \right)\left( {x + 4} \right) - 8m\left( {y - m} \right) = 0\\
\Leftrightarrow \left( {16 - {m^2}} \right)x + 64 - 4{m^2} - 8my + 8{m^2} = 0\\
\Leftrightarrow \left( {16 - {m^2}} \right)x - 8my + 64 + 4{m^2} = 0
\end{array}\)
LG b
Tính khoảng cách từ gốc tọa độ O tới đường thẳng M1M2.
Lời giải chi tiết:
Khoảng cách từ O đến đường thẳng M1M2 là
\(\begin{array}{l}
d\left( {O,{M_1}{M_2}} \right)\\
= \frac{{\left| {\left( {16 - {m^2}} \right).0 - 8m.0 + 64 + 4{m^2}} \right|}}{{\sqrt {{{\left( {16 - {m^2}} \right)}^2} + {{\left( {8m} \right)}^2}} }}\\
= \frac{{\left| {64 + 4{m^2}} \right|}}{{\sqrt {{m^4} + 32{m^2} + {{16}^2}} }}\\
= \frac{{4\left| {{m^2} + 16} \right|}}{{\sqrt {{{\left( {{m^2} + 16} \right)}^2}} }} = \frac{{4\left( {{m^2} + 16} \right)}}{{{m^2} + 16}} = 4
\end{array}\)
LG c
Chứng tỏ rằng đường thẳng M1M2 luôn tiếp xúc với một đường tròn cố định.
Lời giải chi tiết:
* Gọi ( C) là đường tròn tâm O, bán kính R = 4.
=> Đường tròn (C) cố định.
* Theo chứng minh b ta có:
d(O, M1M2) = 4 = R – không phụ thuộc vào m.
=> Đường thẳng M1M2 luôn tiếp xúc với đường tròn (C) cố định.
LG d
Lấy các điểm \({A_1}( - 4;\,0),\,{A_2}(4\,;\,0)\). Tìm tọa độ giao điểm I của hai đường thẳng \({A_1}{M_2},\,{A_2}{M_1}\) .
Lời giải chi tiết:
Phương trình đường thẳng A1M2 là
\({{x + 4} \over 8} = {{y - 0} \over {{{16} \over m}}}\,\,\, \Leftrightarrow \,\,\,2x - my + 8 = 0\)
Phương trình đường thẳng A2M1 là
\({{x - 4} \over { - 8}} = {{y - 0} \over m}\,\,\,\, \Leftrightarrow \,\,\,mx + 8y - 4m = 0\)
Tọa độ giao điểm I của A1M2 và A2M1 là nghiệm của hệ phương trình
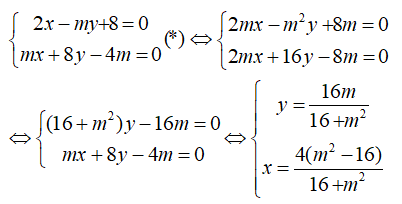
Vậy \(I\left( {{{4({m^2} - 16)} \over {{m^2} + 16}}\,;\,{{16m} \over {{m^2} + 16}}} \right)\) .
LG e
Chứng minh rằng khi m thay đổi, I luôn luôn nằm trên một elip (E) cố định. Xác định tọa độ tiêu điểm của elip đó.
Lời giải chi tiết:
Khử m từ hệ (*) ta có
\(\eqalign{
& \left\{ \matrix{
my = 2x + 8 \hfill \cr
m(4 - x) = 8y \hfill \cr} \right.\cr & \Rightarrow \frac{{2x + 8}}{y} = \frac{{8y}}{{4 - x}}\cr &\Rightarrow (2x + 8).(4 - x) = 8{y^2} \cr
& \Rightarrow \,\,\,2(16 - {x^2}) = 8{y^2}\cr
& \Rightarrow {x^2} + 4{y^2} = 16\cr&\Rightarrow \,\,{{{x^2}} \over {16}} + {{{y^2}} \over 4} = 1 \cr} \)
Vậy I nằm trên elip (E) có phương trình \(\,\,{{{x^2}} \over {16}} + {{{y^2}} \over 4} = 1\) .
Ta có \({c^2} = {a^2} - {b^2} = 16 - 4 = 12\) \( \Rightarrow \,\,c = 2\sqrt 3 \)
Hai tiêu điểm của elip là \({F_1}( - 2\sqrt 3 \,;\,0)\,,\,\,\,{F_2}(2\sqrt 3 \,;\,0)\)
Loigiaihay.com












Danh sách bình luận