 Giải toán 10, giải bài tập Toán 10 Nâng cao, đầy đủ đại số giải tích và hình học
Giải toán 10, giải bài tập Toán 10 Nâng cao, đầy đủ đại số giải tích và hình học
 ÔN TẬP CUỐI NĂM HÌNH HỌC - TOÁN 10 NÂNG CAO
ÔN TẬP CUỐI NĂM HÌNH HỌC - TOÁN 10 NÂNG CAO
Bài 2 trang 126 SGK Hình học 10 nâng cao
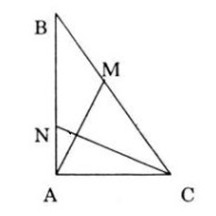
Cho tam giác vuông tại A, AB = c, AC = b . Gọi M là điểm trên cạnh BC sao cho CM = 2BM, N là điểm trên cạnh AB sao cho BN = 2AN (h.106).
Đề bài
Cho tam giác vuông tại A, AB = c, AC = b . Gọi M là điểm trên cạnh BC sao cho CM = 2BM, N là điểm trên cạnh AB sao cho BN = 2AN (h.106).
a) Biểu thị các vectơ theo hai vectơ \(\overrightarrow {AM} ,\,\overrightarrow {CN} \) và \(\overrightarrow {AB} ;\,\overrightarrow {AC} \) .
b) Tìm hệ thức liên hệ giữa b và c sao cho \(AM \bot CN\).
Lời giải chi tiết
a) Ta có:
\(\overrightarrow {CM} = 2\overrightarrow {MB} \) \(\Rightarrow \,\,\overrightarrow {AM} - \overrightarrow {AC} = 2(\overrightarrow {AB} - \overrightarrow {AM} )\)
\(\Rightarrow \,\,\overrightarrow {AM} = {2 \over 3}\overrightarrow {AB} + {1 \over 3}\overrightarrow {AC} \)
Mặt khác \(\overrightarrow {BN} = 2\overrightarrow {NA} \) \( \Rightarrow \,\,\overrightarrow {AN} - \overrightarrow {AB} = - 2\overrightarrow {AN} \)\( \Rightarrow 3\overrightarrow {AN} = \overrightarrow {AB} \)
\(\Rightarrow \,\,\overrightarrow {AN} = {1 \over 3}\overrightarrow {AB} \)
\( \Rightarrow \,\,\overrightarrow {CN} = \overrightarrow {AN} - \overrightarrow {AC} = {1 \over 3}\overrightarrow {AB} - \overrightarrow {AC} \)
Cách khác:
\(\begin{array}{l}
\overrightarrow {CM} = 2\overrightarrow {MB} = 2\left( {\overrightarrow {CB} - \overrightarrow {CM} } \right)\\
= 2\overrightarrow {CB} - 2\overrightarrow {CM} \\
\Rightarrow 3\overrightarrow {CM} = 2\overrightarrow {CB} \\
\Rightarrow \overrightarrow {CM} = \frac{2}{3}\overrightarrow {CB} \\
\Rightarrow \overrightarrow {AM} = \overrightarrow {AC} + \overrightarrow {CM} \\
= \overrightarrow {AC} + \frac{2}{3}\overrightarrow {CB} \\
= \overrightarrow {AC} + \frac{2}{3}\left( {\overrightarrow {AB} - \overrightarrow {AC} } \right)\\
= \frac{2}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC}
\end{array}\)
b) Ta có
\(\eqalign{
& \overrightarrow {AM} \bot \overrightarrow {CN} \Leftrightarrow \,\,\overrightarrow {AM} .\overrightarrow {CN} = 0\cr& \Leftrightarrow \,\,\left( {{2 \over 3}\overrightarrow {AB} + {1 \over 3}\overrightarrow {AC} } \right)\left( {{1 \over 3}\overrightarrow {AB} - \overrightarrow {AC} } \right) \cr&\;\;\;\;\;= 0 \cr
& \Leftrightarrow \,\,{2 \over 9}A{B^2} - {2 \over 3}\overrightarrow {AB} .\overrightarrow {AC} + {1 \over 9}\overrightarrow {AC} .\,\overrightarrow {AB} - {1 \over 3}A{C^2}\cr&\;\;\;\;\; = 0 \cr
& \Leftrightarrow \,\,{2 \over 9}{c^2} - \frac{2}{3}.0 + \frac{1}{9}.0- {1 \over 3}{b^2} = 0 \cr
& \ \Leftrightarrow \,\,2{c^2} = 3{b^2} \cr} \)
Loigiaihay.com












Danh sách bình luận