Áp dụng các trường hợp đồng dạng của tam giác vào tam giác vuông
Có thể áp dụng các trường hợp đồng dạng nào của tam giác vào tam giác vuông? Trường hợp hai cạnh góc vuông là gì? Trường hợp góc – góc trong tam giác vuông là gì?
1. Lý thuyết
- Trường hợp hai cạnh góc vuông:
Nếu hai cạnh góc vuông của tam giác vuông này tỉ lệ với hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
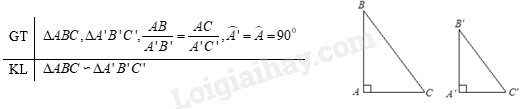
- Trường hợp góc – góc:
Nếu tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
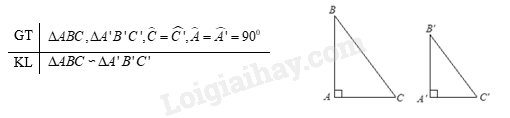
2. Ví dụ minh họa
Ví dụ 1: Cho tam giác ${ABC}$ vuông tại ${A}$ có ${AB = 1}$ cm, ${AC = 3}$ cm. Trên cạnh ${AC}$ lấy ${D}$, ${E}$ sao cho ${AD = DE = EC}$. Chứng minh
a) $\Delta DBE\backsim \Delta DCB$; b) $\widehat{AEB}+\widehat{ACB}={{45}^{0}}$.
Lời giải.
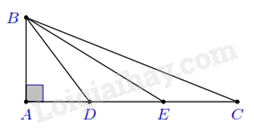
a) Tính được ${DB^2 = 2}$, từ đó ta có
$D{{B}^{2}}=DE\cdot DC\Rightarrow \frac{DB}{DE}=\frac{DC}{DB}\Rightarrow \Delta DBE\backsim \Delta DCB$ (c.g.c).
b) Từ câu a), ta có
$\widehat{AEB}=\widehat{DBC}\text{ }\Rightarrow \widehat{AEB}+\widehat{ACB}=\widehat{DBC}+\widehat{ACB}=\widehat{ADB}={{45}^{0}}$.
Ví dụ 2: Cho tam giác ${ABC}$ vuông tại ${A}$, đường cao ${AH}$. Tia phân giác của ${\widehat{B}}$ cắt ${AH}$, ${AC}$ lần lượt tại ${D}$, ${E}$.
a) Chứng minh $\Delta BAD\backsim \Delta BCE$ và \(\Delta BHD\backsim \Delta BAE\).
b) Chứng minh ${\frac{DH}{DA}=\frac{EA}{EC}}$.
Lời giải
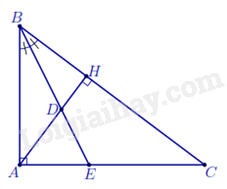
a) Xét $\Delta BAD$ và $\Delta BCE$ có ${\widehat{ABD}=\widehat{EBC}}$ và ${\widehat{BAD}=\widehat{ECB}}$ (góc có cặp cạnh tương ứng vuông góc) $\Rightarrow \Delta BAD\backsim \Delta BCE$ (g.g).
Xét $\Delta BHD$ và $\Delta BAE$ có $\widehat{BHD}=\widehat{BAE}={{90}^{0}}$
và $\widehat{HBD}=\widehat{ABE}\Rightarrow \Delta BAD\backsim \Delta BCE$ (g.g).
b) Từ kết quả câu a), ta có ${\frac{DH}{EA}=\frac{BD}{BE}=\frac{DA}{CE} \Rightarrow \frac{DH}{DA}=\frac{EA}{EC}}$.













Danh sách bình luận