Lý thuyết Toán lớp 8

Lý thuyết Hình chóp tứ giác đều Toán 8

Diện tích xung quanh hình chóp tứ giác đều

Công thức tính diện tích xung quanh của hình chóp tứ giác đều là gì?

1. Lý thuyết

+ Diện tích xung quanh của hình chóp tứ giác đều bằng nữa tích của chu vi đáy với độ dài trung đoạn.

+ Công thức tổng quát : \({S_{xq}} = \frac{1}{2}.C.d\) . Với :

+ \({S_{xq}}\) : Diện tích xung quanh của hình chóp tứ giác đều.

+ Chu vi đáy : C = 4.a (a là độ dài cạnh đáy hình vuông).

+ d: Độ dài trung đoạn của hình chóp tứ giác đều.

2. Ví dụ minh họa

Cho hình chóp tứ giác đều S.ABCD với kích thước như hình vẽ.

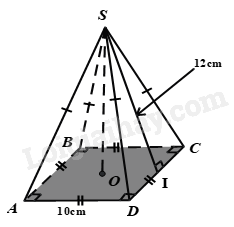
a) Tính chu vi đáy ABCD.

b) Cho biết độ dài trung đoạn hình chóp S.ABC.

c) Tính diện tích xung quanh của hình chóp tứ giác đều S.ABCD.

Lời giải:

a) Chu vi tam giác ABC là: C = 4a = 4.10 = 40 (cm).

b) Độ dài trung đoạn hình chóp S.ABC là d = SI = 12 (cm)

c) Diện tích xung quanh của hình chóp tam giác đều S.ABC là :

\({S_{xq}} = \frac{1}{2}.C.d = \frac{1}{2}.40.12 = 240(c{m^2})\)

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Thể tích của hình chóp tứ giác đều
Công thức tính diện tích xung quanh của hình chóp tứ giác đều là gì?
Hình chóp tứ giác đều
Hình chóp tứ giác đều có đặc điểm gì?

Báo lỗi - Góp ý

Các bài khác cùng chuyên mục

TẢI APP ĐỂ XEM OFFLINE