Giải mục II trang 101, 102 SGK Toán 7 tập 2 - Cánh diều
II. Tính chất
II. Tính chất
HĐ 2
Cho đoạn thẳng AB có trung điểm O, d là đường trung trực của đoạn thẳng AB, điểm M thuộc d, M khác O (Hình 90).
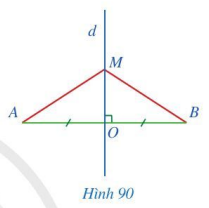
Chứng minh rằng:
a) \(\Delta MOA = \Delta MOB\);
b) MA = MB.
Phương pháp giải:
a) Chứng minh \(\Delta MOA = \Delta MOB\)theo trường hợp c.g.c.
b) Dựa vào kết quả của phần a) để chứng minh MA = MB.
Lời giải chi tiết:
a) Ta có: d là đường trung trực của đoạn thẳng AB, điểm M thuộc d nên MO là đường trung trực của đoạn thẳng AB
\(\Rightarrow MO \bot AB \to \widehat {MOA} = \widehat {MOB} = 90^\circ \).
Xét tam giác MOA và tam giác MOB có:
OM chung;
\(\widehat {MOA} = \widehat {MOB} = 90^\circ \);
OA = OB (O là trung điểm của đoạn thẳng AB).
Vậy \(\Delta MOA = \Delta MOB\) (c.g.c)
b) \(\Delta MOA = \Delta MOB\) nên MA = MB ( 2 cạnh tương ứng)
LT - VD 2
Hình 91 mô tả mặt cắt đứng của một ngôi nhà với hai mái là OA và OB, mái nhà bên trái dài 3 m. Tính chiều dài mái nhà bên phải, biết rằng điểm O thuộc đường trung trực của đoạn thẳng AB.
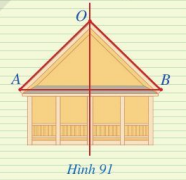
Phương pháp giải:
Dựa vào tính chất của đường trung trực: Một điểm thuộc đường trung trực của đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó.
Lời giải chi tiết:
O thuộc đường trung trực của đoạn thẳng AB nên OA = OB (tính chất đường trung trực của đoạn thẳng).
Vậy suy ra mái nhà bên trái dài 3 m nên mái nhà bên phải cũng dài 3 m.
HĐ 3
Cho đoạn thẳng AB có trung điểm O. Giả sử M là một điểm khác O sao cho MA = MB.
a) Hai tam giác \(\Delta MOA\) và \(\Delta MOB\) có bằng nhau hay không? Vì sao?
b) Đường thẳng MO có là đường trung trực của đoạn thẳng AB hay không? Vì sao?
Phương pháp giải:
a) Chứng minh hai tam giác MOA và MOB bằng nhau theo trường hợp c.c.c.
b) Để xem MO có là đường trung trực của AB hay không, ta tìm mối liên hệ giữa MO và AB.
Lời giải chi tiết:
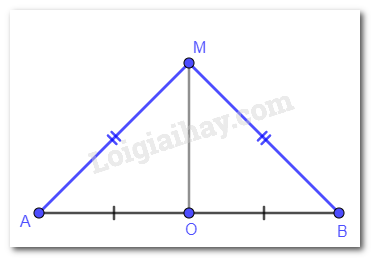
a) Xét hai tam giác MOA và MOB có:
OA = OB (O là trung điểm của AB);
MO chung;
MA = MB.
Vậy \(\Delta MOA = \Delta MOB\)(c.c.c).
b) \(\Delta MOA = \Delta MOB\)nên \(\widehat {MOA} = \widehat {MOB} = \dfrac{1}{2}\widehat {AOB} = 90^\circ \)hay \(MO \bot AB\).
Vậy MO có là đường trung trực của đoạn thẳng AB (MO đi qua trung điểm O của đoạn thẳng AB và vuông góc với đoạn thẳng AB).
LT - VD 3
Cho tam giác ABC cân tại A.
a) Điểm A có thuộc đường trung trực của đoạn thẳng BC hay không? Vì sao?
b) Đường thẳng qua A vuông góc với BC cắt cạnh BC tại H. Đường thẳng AH có là đường trung trực của đoạn thẳng BC hay không? Vì sao?
Phương pháp giải:
a) Dựa vào tính chất của đường thẳng trung trực: Điểm cách đều hai đầu mút của một đoạn thẳng thì nằm trên đường thẳng trung trực của đoạn thẳng đó.
b) Muốn xem đường thẳng AH có là đường trung trực của đoạn thẳng BC hay không, ta tìm mối liên hệ giữa AH với đoạn thẳng BC.
Lời giải chi tiết:
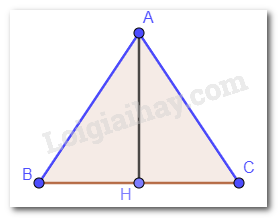
a) Tam giác ABC cân tại A nên AB = AC. Vậy điểm A có thuộc đường trung trực của đoạn thẳng BC.
b) Ta có tam giác ABC cân mà đường thẳng qua A vuông góc với BC cắt BC tại H nên H là trung điểm của BC.
Vậy AH là đường trung trực của đoạn thẳng BC. (AH đi qua trung điểm H của đoạn thẳng BC và vuông góc với đoạn thẳng BC).
Các bài khác cùng chuyên mục
- Tạo đồ dùng dạng hình lăng trụ đứng SGK Toán 7 Cánh diều tập 1
- Giải câu hỏi trang 39, 40 SGK Toán 7 Cánh diều tập 2
- Lý thuyết Trường hợp bằng nhau thứ ba của tam giác: góc-cạnh-góc SGK Toán 7 - Cánh diều
- Lý thuyết Trường hợp bằng nhau thứ hai của tam giác: cạnh-góc-cạnh SGK Toán 7 - Cánh diều
- Lý thuyết Trường hợp bằng nhau thứ nhất của tam giác: cạnh-cạnh-cạnh SGK Toán 7 - Cánh diều
- Tạo đồ dùng dạng hình lăng trụ đứng SGK Toán 7 Cánh diều tập 1
- Giải câu hỏi trang 39, 40 SGK Toán 7 Cánh diều tập 2
- Lý thuyết Trường hợp bằng nhau thứ ba của tam giác: góc-cạnh-góc SGK Toán 7 - Cánh diều
- Lý thuyết Trường hợp bằng nhau thứ hai của tam giác: cạnh-góc-cạnh SGK Toán 7 - Cánh diều
- Lý thuyết Trường hợp bằng nhau thứ nhất của tam giác: cạnh-cạnh-cạnh SGK Toán 7 - Cánh diều













Danh sách bình luận