Bài 3. Phép cộng, phép trừ đa thức một biến trang 54 SG..

Giải bài 4 trang 59 SGK Toán 7 tập 2 - Cánh diều

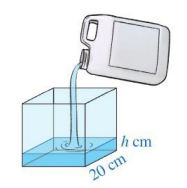
Người ta rót nước từ một can đựng 10 lít sang một bể rỗng có dạng hình lập phương với độ dài cạnh 20cm. Khi mực nước trong bể cao h (cm) thì thể tích nước trong can còn lại là bao nhiêu? Biết rằng 1 lít = 1 dm3

Đề bài

Người ta rót nước từ một can đựng 10 lít sang một bể rỗng có dạng hình lập phương với độ dài cạnh 20cm. Khi mực nước trong bể cao h (cm) thì thể tích nước trong can còn lại là bao nhiêu? Biết rằng 1 lít = 1\(d{m^3}\).

Phương pháp giải - Xem chi tiết

Để tính được thể tích nước còn lại trong can, ta tính thể tích của chiếc bể đến độ cao h. (Đồng nghĩa với việc tính thể tích hình hộp chữ nhật, đáy là hình vuông cạnh 20 cm và chiều cao bằng h). Rồi lấy thể tích của nước trong can ban đầu trừ đi thể tích của chiếc bể đến độ cao h.

Chú ý: Đổi đơn vị cm sang dm.

Lời giải chi tiết

Đổi 20 cm = 2 dm; h cm = \(\dfrac{h}{10}\) dm.

Thể tích của phần nước trong bể khi mực nước cao h (cm) là:

\(2.2.\dfrac{h}{10} = 0,4.h(d{m^3})=0,4.h\) (lít)

Vậy khi mực nước trong bể cao h (cm) thì thể tích nước trong can còn lại là:

\(10 - 0,4.h\) (lít)

Bình luận

Chia sẻ

Bình chọn:

4.6 trên 24 phiếu

Bài tiếp theo

Giải bài 5 trang 59 SGK Toán 7 tập 2 - Cánh diều
Bạn Minh cho rằng “Tổng của hai đa thức bậc bốn luôn luôn là đa thức bậc bốn”. Bạn Quân cho rằng “Hiệu của hai đa thức bậc bốn luôn luôn là đa thức bậc bốn”. Hai bạn Minh và Quân nói như vậy có đúng không? Giải thích vì sao.
Giải bài 3 trang 59 SGK Toán 7 tập 2 - Cánh diều
Bác Ngọc gửi ngân hàng thứ nhất 90 triệu đồng với kì hạn 1 năm, lãi suất x%/năm. Bác Ngọc gửi ngân hàng thứ hai 80 triệu đồng với kì hạn 1 năm, lãi suất (x + 1,5)%/năm. Hết kì hạn 1 năm, bác Ngọc có được cả gốc lẫn lãi là bao nhiêu: a) Ở ngân hàng thứ hai? B) Ở cả hai ngân hàng?
Giải bài 2 trang 59 SGK Toán 7 tập 2 - Cánh diều
Xác định bậc của hai đa thức là tổng, hiệu của:
Giải bài 1 trang 59 SGK Toán 7 tập 2 - Cánh diều
Cho hai đa thức:
Giải mục II trang 57, 58, 59 SGK Toán 7 tập 2 - Cánh diều
a) Thực hiện phép trừ trong mỗi trường hợp sau: b) Nêu quy tắc trừ hai đơn thức có cùng số mũ của biến.
Giải mục I trang 54,55,56 SGK Toán 7 tập 2 - Cánh diều
a) Thực hiện phép cộng trong mỗi trường hợp sau b) Nêu quy tắc cộng hai đơn thức có cùng số mũ của biến.
Giải câu hỏi khởi động trang 54 SGK Toán 7 tập 2 - Cánh diều
Một số tình huống trong cuộc sống dẫn đến việc cộng, trừ hai đa thức một biến, chẳng hạn, ta phải tính tổng diện tích các mặt của hình hộp chữ nhật (Hình 2) có độ dài hai cạnh đáy là x (m), 2x (m) và chiều cao là 2 (m).