-
GIẢI SGK TOÁN 8 KẾT NỐI TRI THỨC - MỚI NHẤT
-
Toán 7 tập 1 - Kết nối tri thức với cuộc sống
-
Chương I. Số hữu tỉ
-
Chương II. Số thực
-
Chương III. Góc và đường thẳng song song
-
Chương IV. Tam giác bằng nhau
- Bài 12. Tổng các góc trong một tam giác
- Bài 13. Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác
- Luyện tập chung trang 68
- Bài 14. Trường hợp bằng nhau thứ hai và thứ ba của tam giác
- Luyện tập chung trang 74
- Bài 15. Các trường hợp bằng nhau của tam giác vuông
- Bài 16. Tam giác cân. Đường trung trực của đoạn thẳng
- Luyện tập chung trang 85
- Bài tập cuối chương IV
-
Chương V. Thu thập và biểu diễn dữ liệu
-
Hoạt động thực hành trải nghiệm
-
-
Toán 7 tập 2 - Kết nối tri thức với cuộc sống
-
Chương VI. Tỉ lệ thức và đại lượng tỉ lệ
-
Chương VII. Biểu thức đại số và đa thức một biến
-
Chương VIII. Làm quen với biến cố và xác suất của biến cố
-
Chương IX. Quan hệ giữa các yếu tố trong tam giác
- Bài 31. Quan hệ giữa góc và cạnh đối diện trong một tam giác
- Bài 32. Quan hệ giữa đường vuông góc và đường xiên
- Bài 33. Quan hệ giữa ba cạnh của một tam giác
- Luyện tập chung trang 70
- Bài 34. Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác
- Bài 35. Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác
- Luyện tập chung trang 82
- Bài tập cuối chương IX
-
Chương X. Một số hình khối trong thực tiễn
-
Hoạt động thực hành trải nghiệm tập 2
-
Toán 7, giải toán lớp 7 kết nối tri thức với cuộc sống
Bài tập cuối chương III trang 59 SGK Toán 7 kết nối tri..
Giải bài 3.32 trang 59 SGK Toán 7 tập 1 - Kết nối tri thức
Chứng minh rằng: Cho điểm A và đường thẳng d thì có duy nhất đường thẳng đi qua A và vuông góc với d, tức là nếu có hai đường thẳng đi qua A vuông góc với d thì chúng phải trùng nhau.
Tổng hợp đề thi học kì 2 lớp 7 tất cả các môn - Kết nối tri thức
Toán - Văn - Anh - Khoa học tự nhiên...
Đề bài
Chứng minh rằng: Cho điểm A và đường thẳng d thì có duy nhất đường thẳng đi qua A và vuông góc với d, tức là nếu có hai đường thẳng đi qua A vuông góc với d thì chúng phải trùng nhau.
Phương pháp giải - Xem chi tiết
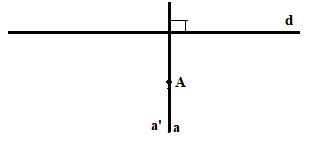
Giả sử có 2 đường thẳng đi qua A và vuông góc với d. Ta sẽ chứng minh 2 đường này trùng nhau.
Lời giải chi tiết
Giả sử có 2 đường thẳng a và a’ đi qua A và vuông góc với d.
Vì a \( \bot \) d, mà a’ \( \bot \) d nên a // a’ (hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì song song với nhau)
Mà A \( \in \) a, A \( \in \) a'
\( \Rightarrow a \equiv a'\)
Vậy có duy nhất đường thẳng đi qua A và vuông góc với d.
Bình luận
Chia sẻ
Luyện Bài Tập Trắc nghiệm Toán 7 - Kết nối tri thức - Xem ngay
>> Học trực tuyến lớp 8 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều). Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả.
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục
- Lý thuyết quan hệ giữa ba cạnh của một tam giác Toán 7 Kết nối tri thức
- Lý thuyết quan hệ giữa đường vuông góc và đường xiên Toán 7 Kết nối tri thức
- Lý thuyết quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu Toán 7 Kết nối tri thức
- Lý thuyết quan hệ giữa góc và cạnh đối diện trong một tam giác Toán 7 Kết nối tri thức
- Giải câu hỏi trang 108, 109 SGK Toán 7 Kết nối tri thức với cuộc sống tập 2
- Lý thuyết quan hệ giữa ba cạnh của một tam giác Toán 7 Kết nối tri thức
- Lý thuyết quan hệ giữa đường vuông góc và đường xiên Toán 7 Kết nối tri thức
- Lý thuyết quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu Toán 7 Kết nối tri thức
- Lý thuyết quan hệ giữa góc và cạnh đối diện trong một tam giác Toán 7 Kết nối tri thức
- Giải câu hỏi trang 108, 109 SGK Toán 7 Kết nối tri thức với cuộc sống tập 2
