Giải bài 3.3 trang 45 SGK Toán 7 tập 1 - Kết nối tri thức

Vẽ góc xOy có số đo bằng 60 độ. Vẽ tia Om là tia đối của tia Ox. a) Gọi tên hai góc kề bù có trong hình vừa vẽ. b) Tính số đo góc yOm. c) Vẽ tia Ot là tia phân giác của góc xOy. Tính số đo các góc tOy và tOm.

Tổng hợp đề thi học kì 2 lớp 7 tất cả các môn - Kết nối tri thức

Toán - Văn - Anh - Khoa học tự nhiên...

Đề bài

Vẽ góc xOy có số đo bằng 60 \(^\circ \). Vẽ tia Om là tia đối của tia Ox.

a) Gọi tên hai góc kề bù có trong hình vừa vẽ.

b) Tính số đo góc yOm.

c) Vẽ tia Ot là tia phân giác của góc xOy. Tính số đo các góc tOy và tOm.

Phương pháp giải - Xem chi tiết

* Vẽ hình theo mô tả

* 2 góc có một cạnh chung, hai cạnh còn lại là hai tia đối nhau được gọi là 2 góc kề bù.

* Sử dụng tính chất: + Tổng của 2 góc kề bù là 180 độ.

+ Khi Om là tia phân giác của góc xOy thì \(\widehat {xOm} = \widehat {mOy} = \frac{1}{2}.\widehat {xOy}\)

Lời giải chi tiết

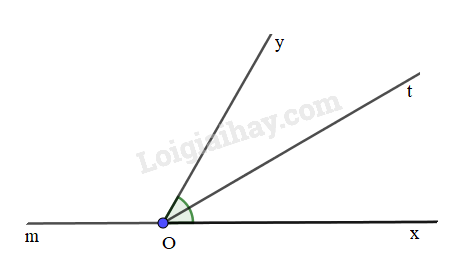
a) Hai góc kề bù có trên hình vừa vẽ là góc xOy và mOy

b) Vì \(\widehat {xOy} + \widehat {yOm} = 180^\circ \) (2 góc kề bù)

\(\begin{array}{l} \Rightarrow 60^\circ + \widehat {yOm} = 180^\circ \\ \Rightarrow \widehat {yOm} = 180^\circ - 60^\circ = 120^\circ \end{array}\)

c) Vì tia Ot là tia phân giác của góc xOy nên \(\widehat {xOt} = \widehat {tOy} = \frac{1}{2}.\widehat {xOy} = \frac{1}{2}.60^\circ = 30^\circ \)

Mà \(\widehat {xOt}\) và \(\widehat {tOm}\) là hai góc kề bù nên

\(\begin{array}{l}\widehat {xOt} + \widehat {tOm} = 180^\circ \\ \Rightarrow 30^\circ + \widehat {tOm} = 180^\circ \\ \Rightarrow \widehat {tOm} = 180^\circ - 30^\circ = 150^\circ \end{array}\)

Vậy \(\widehat {tOy} = 30^\circ ;\widehat {tOm} = 150^\circ \)

Bình luận

Chia sẻ

Bình chọn:

4.5 trên 142 phiếu

Bài tiếp theo

Giải bài 3.4 trang 45 SGK Toán 7 tập 1 - Kết nối tri thức
Cho Hình 3.15a, biết DMA=45 độ. Tính số đo góc DMB
Giải bài 3.5 trang 45 SGK Toán 7 tập 1 - Kết nối tri thức
Cho Hình 3.15b, biết xBm=36 độ. Tính số đo các góc còn lại trong hình vừa vẽ.
Giải bài 3.2 trang 45 SGK Toán 7 tập 1 - Kết nối tri thức
Cho Hình 3.14, hãy kể tên các cặp góc đối đỉnh.
Giải bài 3.1 trang 45 SGK Toán 7 tập 1 - Kết nối tri thức
Cho Hình 3.13, hãy kể tên các cặp góc kề bù.
Giải mục 2 trang 43, 44, 45 SGK Toán 7 tập 1 - Kết nối tri thức
Cắt rời một góc xOy từ một tờ giấy rồi gấp sao cho hai cạnh của góc trùng nhau (H.3.9).....Cho góc xAm có số đo bằng..
Giải mục 1 trang 41, 42, 43 SGK Toán 7 tập 1 - Kết nối tri thức
Quan sát hình vẽ bên. Em hãy nhận xét về mối quan hệ về đỉnh, về cạnh của hai góc được đánh dấu...Cho ba tia Ox, Oy, Oz như Hình 3.1, trong đó Ox và Oy là hai tia đối nhau. a) Em hãy nhận xét về quan hệ về đỉnh, về cạnh của hai góc xOz và zOy. b) Đo rồi tính tổng số đo góc hai góc xOz và zOy.
Lý thuyết Góc ở vị trí đặc biệt. Tia phân giác của một góc SGK Toán 7 - Kết nối tri thức
1. Góc ở vị trí đặc biệt

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 7 - Kết nối tri thức - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

>> Học trực tuyến lớp 8 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều). Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả.