Bài 3. Hai đường thẳng song song trang 100 SGK Toán 7 c..

Giải bài 1 trang 104 SGK Toán 7 tập 1 - Cánh diều

Quan sát hình 44, biết a // b.

Đề bài

Quan sát hình 44, biết a // b.

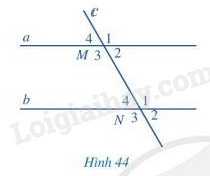
a) So sánh \(\widehat {{M_1}}\) và \(\widehat {{N_3}}\); \(\widehat {{M_4}}\) và \(\widehat {{N_2}}\) ( mỗi cặp góc M₁ và N₃, M₄ và N₂ gọi là một cặp góc so le ngoài)

b) Tính: \(\widehat {{M_2}} + \widehat {{N_1}}\) và \(\widehat {{M_3}} + \widehat {{N_4}}\) ( mỗi cặp góc M₂ và N₁, M₃ và N₄ gọi là một cặp góc trong cùng phía)

Phương pháp giải - Xem chi tiết

+ 1 đường thẳng cắt 2 đường thẳng song song tạo ra các cặp góc so le trong bằng nhau, đồng vị bằng nhau.

+ 2 góc đối đỉnh thì bằng nhau.

+ 2 góc kề bù có tổng số đo bằng 180\(^\circ \)

Lời giải chi tiết

a) Vì a // b nên \(\widehat {{M_1}} = \widehat {{N_1}}\); \(\widehat {{M_4}} = \widehat {{N_4}}\) ( 2 góc đồng vị) mà \(\widehat {{N_3}} = \widehat {{N_1}}\) ; \(\widehat {{N_4}} = \widehat {{N_2}}\) ( 2 góc đối đỉnh) nên \(\widehat {{M_1}}\) =\(\widehat {{N_3}}\); \(\widehat {{M_4}}\) =\(\widehat {{N_2}}\)

b) Vì a // b nên \(\widehat {{M_2}} = \widehat {{N_2}};\widehat {{M_3}} = \widehat {{N_3}}\) ( 2 góc đồng vị), mà \(\widehat {{N_1}} + \widehat {{N_2}} = 180^\circ ;\widehat {{N_3}} + \widehat {{N_4}} = 180^\circ \) ( 2 góc kề bù) nên \(\widehat {{M_2}} + \widehat {{N_1}}\) = 180\(^\circ \); \(\widehat {{M_3}} + \widehat {{N_4}}\)= 180\(^\circ \)

Chú ý:

Nếu đường thẳng c cắt cả hai đường thẳng song song a và b thì:

+ Hai góc so le ngoài bằng nhau

+ Hai góc trong cùng phía có tổng số đo bằng 180\(^\circ \)

Bình luận

Chia sẻ

Bình chọn:

4.7 trên 65 phiếu

Bài tiếp theo

Giải bài 2 trang 104 SGK Toán 7 tập 1 - Cánh diều
Quan sát Hình 45. a) Vì sao hai đường thẳng a và b song song với nhau? b) Tính số đo góc BCD.
Giải bài 3 trang 104 SGK Toán 7 tập 1 - Cánh diều
Để đảm bảo an toàn khi đi lại trên cầu thang của ngôi nhà, người ta phải làm lan can. Phía trên của lan can có tay vịn làm chỗ dựa để khi lên xuống cầu thang được thuận tiện. Phía dưới tay vịn là các thanh trụ song song với nhau và các thanh sườn song song với nhau. Để đảm bảo chắc chắn thì các thanh trụ của lan can được gắn vuông góc cố định xuống bậc cầu thang.
Giải mục IV trang 103 SGK Toán 7 tập 1 - Cánh diều
Tìm số đo x trong Hình 43, biết u // v
Giải mục II trang 101, 102 SGK Toán 7 tập 1 - Cánh diều
Quan sát các Hình 38a, 38b, 38c và đoán xem các đường thẳng nào song song với nhau.
Giải câu hỏi khởi động trang 100 SGK Toán 7 tập 1 - Cánh diều
Hình 33 minh họa góc quan sát của người phi công và góc quan sát của người hoa tiêu khi hướng dẫn máy bay bay vào vị trí ở sân bay
Lý thuyết Hai đường thẳng song song SGK Toán 7 Cánh diều
I. Hai góc đồng vị. Hai góc so le trong