Đề ôn hè Toán 6 lên 7 - Đề 9

Đề bài

Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:

Câu 1: Tổng tất cả các số nguyên thoả mãn \( - 5 \le x \le 6\) là:

A. 1.

B. 6.

C. -5.

D. 0.

Câu 2: Một lớp học có 24 học sinh nam và 18 học sinh nữ thì số cách chia tổ mà số nam và số nữ được chia đều vào các tổ là:

A. 4.

B. 3.

C. 2.

D. 1.

Câu 3: Trong các hình sau, hình có nhiều trục đối xứng nhất là:

A. Hình trái tim.

B. Hình vuông.

C. Hình tròn.

D. Hình tam giác đều.

Câu 4: Cá chuồn là loài cá sinh sống ở biển, có thể bơi dưới nước, khi bị truy đuổi nó có thể vọt lên khỏi mặt nước và bay một đoạn để trốn tránh. Nếu một con cá chuồn đang ở vị trí \(165\,cm\) dưới mực nước biển và bay vọt lên theo phương thẳng đứng \(285\,cm\) thì khi đó vị trí của nó so với mực nước biển là:

A. \(450\,cm\).

B. \(165\,cm\).

C. \(165\,cm\).

D. \(120\,cm\).

Câu 5: Rút gọn phân số \(\frac{{ - 27}}{{63}}\) đến phân số tối giản là:

A. \(\frac{9}{{21}}\).

B. \(\frac{{ - 9}}{{21}}\).

C. \(\frac{3}{7}\).

D. \(\frac{{ - 3}}{7}\).

Câu 6: Làm tròn số 76,421 đến hàng phần mười ta được kết quả là:

A. 76.

B. 76,5.

C. 76,4.

D. 76,42.

Câu 7: Biết 75% của một sợi dây là 9 mét thì sợi dây có chiều dài là:

A. 6,75 mét.

B. 12 mét.

C. 5,41 mét.

D. 6,85 mét.

Câu 8: Minh gieo một con xúc xắc 100 lần và ghi lại số chấm xuất hiện ở mỗi lần gieo được kết quả như sau:

Tính xác suất thực nghiệm của sự kiện “Số chấm xuất hiện là số chẵn” là:

A. 0,57.

B. 0,37.

C. 0,44.

D. 0,43.

Câu 9: Mỗi xúc xắc có 6 mặt, số chấm ở mỗi mặt là một trong các số nguyên dương từ 1 đến 6. Gieo xúc xắc một lần. Mặt xuất hiện của xúc xắc là phần tử của tập hợp nào dưới đây?

A. {1; 6}.

B. {0; 1; 2; 3; 4; 5; 6}.

C. {0; 1; 2; 3; 4; 5}.

D. {1; 2; 3; 4; 5; 6}.

Câu 10: Điểm M là trung điểm của AB nếu:

A. MA = MB.

B. M nằm giữa A và B.

C. MA = MB = \(\frac{{AB}}{2}\).

D. AM + MB = AB.

Câu 11: Cho góc xOy bằng \(100^\circ \) thì góc xOy là:

A. Góc nhọn.

B. Góc vuông.

C. Góc tù.

D. Góc bẹt.

Câu 12: Trong hình vẽ sau, khẳng định sai là:

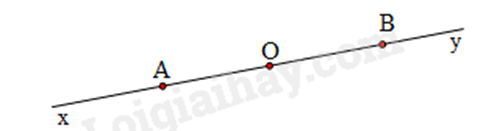
A. Hai tia BO và By đối nhau.

B. Hai tia AO và OB trùng nhau.

C. Hai tia AO và AB trùng nhau.

D. Hai tia Ax và AB đối nhau.

Phần tự luận (7 điểm)

Bài 1. (1 điểm) Thực hiện phép tính một cách hợp lý (nếu có thể)

a) \(240:\left[ {{{\left( {19 - 17} \right)}^2} - 124} \right] + {2025^0}\)

b) \(0,75 - \left( {2\frac{1}{3} + 0,75} \right) + 9 \cdot \left( { - \frac{1}{9}} \right)\)

Bài 2. (1,5 điểm) Tìm \(x\), biết:

a) \(x + 9,25 = 17,75\)

b) \(\frac{2}{3}x - \frac{5}{7} = \frac{9}{7}\)

c) \(x \vdots {\rm{ 12, }}x \vdots {\rm{ 21,}}\,x \vdots \,\,{\rm{28}}\) và \(150 < x < 200\)

Bài 3. (1,5 điểm) Sắp đến hè, để giúp Nam tập luyện môn cầu lông, mẹ của Nam đã mua cho Nam một cây vợt cầu lông và một hộp cầu có \(20\) quả hết \(990\,000\) đồng (đã bao gồm thuế VAT). Trong đó, cây vợt có giá \(560\,000\) đồng (chưa có thuế VAT). Mẹ Nam mua ở siêu thị nên tất cả các mặt hàng người mua đều phải trả thêm thuế giá trị gia tăng VAT là \(10{\rm{\% }}\).

a) Tính giá tiền của cây vợt bao gồm thuế VAT mà mẹ của Nam đã mua.

b) Tính giá của mỗi quả cầu lông khi chưa tính thuế VAT.

Bài 4. (1,5 điểm) Một mảnh đất hình chữ nhật có chiều dài là 24m, chiều rộng 20m. Người ta chia mảnh đất thành hai khu, một khu trồng hoa và một khu trồng cỏ. Hoa sẽ trồng trong khu vực hình bình hành và cỏ trồng ở phần đất còn lại (như hình vẽ).

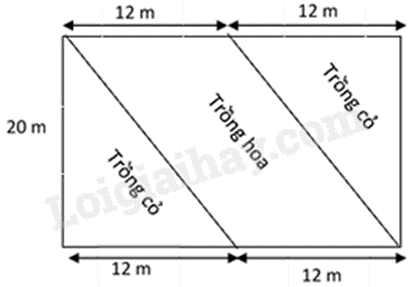
a) Tính diện tích mảnh đất hình chữ nhật.

b) Tính số tiền cần trả để trồng cỏ, biết giá mỗi mét vuông trồng cỏ là 40 000 đồng.

Bài 5. (1,5 điểm) Cho đoạn thẳng \(AB = 9cm\). Lấy điểm \(C\) thuộc đoạn thẳng \(AB\) sao cho \(AC = 3cm\).

a) Tính độ dài đoạn thẳng \(BC\).

b) Lấy điểm \(M\) nằm giữa hai điểm \(C\) và \(B\) sao cho \(C\) là trung điểm của đoạn thẳng \(AM\). Tính \(AM\).

c) Lấy điểm \(O\) nằm ngoài đường thẳng \(AB\). Vẽ các đoạn thẳng \(OA,OB,OC\). Nêu tên các góc đỉnh \(O\) trên hình vẽ.

-------- Hết --------

Lời giải

Phần trắc nghiệm

Câu 1: Tổng tất cả các số nguyên thoả mãn \( - 5 \le x \le 6\) là:

A. 1.

B. 6.

C. -5.

D. 0.

Phương pháp

Xác định các giá trị của \(x\) thoả mãn.

Tính tổng các giá trị của \(x\).

Lời giải

Các số nguyên \(x\) thoả mãn \( - 5 \le x \le 6\) là: -5; -4; -3; -2; -1; 0; 1; 2; 3; 4; 5; 6.

Do đó tổng các số nguyên \(x\) là:

(-5) + (-4) + (-3) + (-2) + (-1) + 0 + 1 + 2 + 3 + 4 + 5 + 6

= (-5 + 5) + (-4 + 4) + (-3 + 3) + (-2 + 2) + (-1 + 1) + 0 + 6

= 0 + 0 + 0 + 0 + 0 + 6 = 6.

Đáp án: B

Câu 2: Một lớp học có 24 học sinh nam và 18 học sinh nữ thì số cách chia tổ mà số nam và số nữ được chia đều vào các tổ là:

A. 4.

B. 3.

C. 2.

D. 1.

Phương pháp

Vì số nam và số nữ được chia đều vào các tổ nên số cách chia tổ là ước chung của 24 và 18.

Phân tích 24 và 18 để tìm ƯCLN(24;18) từ đó suy ra các ƯC(24; 18).

Lời giải

Vì số nam và số nữ được chia đều vào các tổ nên số cách chia tổ là ước chung của 24 và 18.

Ta có: 24 = 2\(^3\).3; 18 = 2.3\(^2\)

Do đó ƯCLN(24;18) = 2.3 = 6

Suy ra ƯC(24; 18) = \(\left\{ {1;2;3;6} \right\}\).

Vậy có 4 cách chia tổ.

Đáp án: A

Câu 3: Trong các hình sau, hình có nhiều trục đối xứng nhất là:

A. Hình trái tim.

B. Hình vuông.

C. Hình tròn.

D. Hình tam giác đều.

Phương pháp

Dựa vào kiến thức về trục đối xứng: Trục đối xứng là đường thẳng chia hình thành hai phần mà khi ta “gấp” hình theo đường thẳng đó thì hai phần “chồng khít” lên nhau.

Lời giải

Hình có nhiều trục đối xứng nhất là Hình tròn. Hình tròn có vô số trục đối xứng.

Đáp án: C

Câu 4: Cá chuồn là loài cá sinh sống ở biển, có thể bơi dưới nước, khi bị truy đuổi nó có thể vọt lên khỏi mặt nước và bay một đoạn để trốn tránh. Nếu một con cá chuồn đang ở vị trí \(165\,cm\) dưới mực nước biển và bay vọt lên theo phương thẳng đứng \(285\,cm\) thì khi đó vị trí của nó so với mực nước biển là:

A. \(450\,cm\).

B. \(165\,cm\).

C. \(165\,cm\).

D. \(120\,cm\).

Phương pháp

Dưới mực nước biển ta biểu diễn bằng số âm.

Sử dụng quy tắc cộng hai số nguyên khác dấu.

Lời giải

Vì con cá chuồn đang ở vị trí 165cm dưới mực nước biển nên ta biểu diễn bằng số - 165.

Vì con cá chuồn bay vọt lên theo phương thẳng đứng 285cm nên vị trí của nó so với mực nước biển là:

(-165) + 285 = 120 (cm).

Đáp án: D

Câu 5: Rút gọn phân số \(\frac{{ - 27}}{{63}}\) đến phân số tối giản là:

A. \(\frac{9}{{21}}\).

B. \(\frac{{ - 9}}{{21}}\).

C. \(\frac{3}{7}\).

D. \(\frac{{ - 3}}{7}\).

Phương pháp

Tìm ƯCLN của tử và mẫu (không tính dấu “-”) rồi chia cả tử và mẫu cho ƯCLN đó.

Lời giải

Ta có: 27 = 3\(^3\); 63 = 3\(^2\).7 nên ƯCLN(27;63) = 3\(^2\) = 9

Rút gọn phân số \(\frac{{ - 27}}{{63}}\) đến phân số tối giản ta được: \(\frac{{ - 27}}{{63}} = \frac{{ - 27:9}}{{63:9}} = \frac{{ - 3}}{7}\).

Đáp án: D

Câu 6: Làm tròn số 76,421 đến hàng phần mười ta được kết quả là:

A. 76.

B. 76,5.

C. 76,4.

D. 76,42.

Phương pháp

* Làm tròn số thập phân dương:

- Đối với chữ số hàng làm tròn:

    + Giữ nguyên nếu chữ số ngay bên phải nhỏ hơn 5;

    + Tăng 1 đơn vị nếu chữ số ngay bên phải lớn hơn hoặc bằng 5

- Đối với chữ số sau hàng làm tròn:

    + Bỏ đi nếu ở phần thập phân;

    + Thay bằng các chữ số 0 nếu ở phần số nguyên.

Lời giải

Chữ số ở hàng phần mười là chữ số 4.

Chữ số ngay bên phải chữ số 4 là chữ số 2 < 5 nên ta giữ nguyên chữ số 4.

Vậy số 76,421 làm tròn đến hàng phần mười ta được kết quả là 76,4.

Đáp án: C

Câu 7: Biết 75% của một sợi dây là 9 mét thì sợi dây có chiều dài là:

A. 6,75 mét.

B. 12 mét.

C. 5,41 mét.

D. 6,85 mét.

Phương pháp

Tìm số a khi biết m% của a là b, ta tính: \(a = b:\frac{m}{{100}}\).

Lời giải

Sợi dây có chiều dài là: \(9:\frac{{75}}{{100}} = 12\) (mét)

Đáp án: B

Câu 8: Minh gieo một con xúc xắc 100 lần và ghi lại số chấm xuất hiện ở mỗi lần gieo được kết quả như sau:

Tính xác suất thực nghiệm của sự kiện “Số chấm xuất hiện là số chẵn” là:

A. 0,57.

B. 0,37.

C. 0,44.

D. 0,43.

Phương pháp

Tính số lần số chấm xuất hiện là số chẵn.

Xác suất thực nghiệm của sự kiện bằng tỉ lệ giữa số lần xuất hiện sự kiện với tổng số lần thực hiện.

Lời giải

Số lần gieo mà số chấm xuất hiện là số chẵn là:

20 + 22 + 15 = 57 (lần)

Xác suất thực nghiệm của sự kiện “Số chấm xuất hiện là số chẵn” là:

\(\frac{{57}}{{100}} = 0,57\).

Đáp án: A

Câu 9: Mỗi xúc xắc có 6 mặt, số chấm ở mỗi mặt là một trong các số nguyên dương từ 1 đến 6. Gieo xúc xắc một lần. Mặt xuất hiện của xúc xắc là phần tử của tập hợp nào dưới đây?

A. {1; 6}.

B. {0; 1; 2; 3; 4; 5; 6}.

C. {0; 1; 2; 3; 4; 5}.

D. {1; 2; 3; 4; 5; 6}.

Phương pháp

Xác định các mặt của con xúc xắc.

Lời giải

Mặt xuất hiện của xúc xắc là phần tử của tập hợp {1; 2; 3; 4; 5; 6} do số chấm ở mỗi mặt là một trong các số nguyên dương từ 1 đến 6.

Đáp án: D

Câu 10: Điểm M là trung điểm của AB nếu:

A. MA = MB.

B. M nằm giữa A và B.

C. MA = MB = \(\frac{{AB}}{2}\).

D. AM + MB = AB.

Phương pháp

Trung điểm của đoạn thẳng là điểm nằm giữa và cách đều hai đầu đoạn thẳng. Trung điểm của đoạn thẳng còn gọi là điểm chính giữa của đoạn thẳng.

Lời giải

Điểm M là trung điểm của AB nếu MA = MB = \(\frac{{AB}}{2}\).

Đáp án: C

Câu 11: Cho góc xOy bằng \(100^\circ \) thì góc xOy là:

A. Góc nhọn.

B. Góc vuông.

C. Góc tù.

D. Góc bẹt.

Phương pháp

Góc nhọn là góc có số đo nhỏ hơn \(90^\circ \).

Góc vuông là góc có số đo bằng \(90^\circ \).

Góc tù là góc có số đo lớn hơn \(90^\circ \).

Góc bẹt là góc có số đo bằng \(180^\circ \).

Lời giải

Vì \(180^\circ  > 100^\circ  > 90^\circ \) nên góc xOy là góc tù.

Đáp án: C

Câu 12: Trong hình vẽ sau, khẳng định sai là:

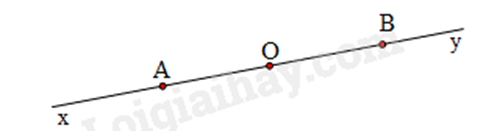
A. Hai tia BO và By đối nhau.

B. Hai tia AO và OB trùng nhau.

C. Hai tia AO và AB trùng nhau.

D. Hai tia Ax và AB đối nhau.

Phương pháp

Hai tia chung gốc Ox và Oy tạo thành một đường thẳng xy gọi là hai tia đối nhau.

Hai tia trùng nhau là hai tia chung gốc và cùng nằm 1 phía trên 1 đường thẳng.

Lời giải

Hai tia BO và By đối nhau vì chúng tạo thành đương thẳng Oy.

Hai tia AO và OB không chung gốc nên không trùng nhau nên B sai.

Hai tia AO và AB trùng nhau vì O và B cùng nằm một phía trên đường thẳng.

Hai tia Ax và AB đối nhau vì chúng tạo thành đường thẳng Bx.

Đáp án: B

Phần tự luận.

Bài 1. (1 điểm) Thực hiện phép tính một cách hợp lý (nếu có thể)

a) \(240:\left[ {{{\left( {19 - 17} \right)}^2} - 124} \right] + {2025^0}\)

b) \(0,75 - \left( {2\frac{1}{3} + 0,75} \right) + 9 \cdot \left( { - \frac{1}{9}} \right)\)

Phương pháp

a) Thực hiện phép tính theo đúng thứ tự.

b) Bỏ ngoặc và nhóm số hợp lý.

Lời giải

a) \(240:\left[ {{{\left( {19 - 17} \right)}^2} - 124} \right] + {2025^0}\)

\(\begin{array}{l} = 240:\left[ {{{\left( 2 \right)}^2} - 124} \right] + 1\\ = 240:\left[ {4 - 124} \right] + 1\\ = 240:\left( { - 120} \right) + 1\\ = \left( { - 2} \right) + 1\\ =  - 1\end{array}\)

b) \(0,75 - \left( {2\frac{1}{3} + 0,75} \right) + 9.\left( { - \frac{1}{9}} \right)\)

\( = 0,75 - \frac{7}{3} - 0,75 - 1\)

\( = \left( {0,75 - 0,75} \right) - \frac{7}{3} - 1\)

\( =  - \frac{7}{3} - \frac{3}{3} =  - \frac{{10}}{3}\)

Bài 2. (1,5 điểm) Tìm \(x\), biết:

a) \(x + 9,25 = 17,75\)

b) \(\frac{2}{3}x - \frac{5}{7} = \frac{9}{7}\)

c) \(x \vdots {\rm{ 12, }}x \vdots {\rm{ 21,}}\,x \vdots \,\,{\rm{28}}\) và \(150 < x < 200\)

Phương pháp

a, b) Chuyển vế, đổi dấu và thực hiện phép tính.

c) Chỉ ra x là BC(12;21;28)

Phân tích 12; 21; 28 để tìm BCNN, suy ra BC = B(BCNN).

Kết hợp điều kiện \(150 < x < 200\) để tìm \(x\).

Lời giải

a) \(x + 9,25 = 17,75\)

\(x = 17,75 - 9,25\)

\(x = 8,5\)

Vậy \(x = 8,5\).

b) \(\frac{2}{3}x - \frac{5}{7} = \frac{3}{7}\)

\(\frac{2}{3}x = \frac{3}{7} + \frac{5}{7}\)

\(\frac{2}{3}x = \frac{8}{7}\)

\(x = \frac{{12}}{7}\)

Vậy \(x = \frac{{12}}{7}\).

c) Vì \(x \vdots {\rm{ 12, }}x \vdots {\rm{ 21,}}\,x \vdots \,\,{\rm{28}}\) nên \(x \in BC(12,21,28)\)

BCNN(12,21,28) = 84

BC(12,21,28) = {0; 84; 168; 252; …}

mà \(150 < x < 200\)

nên x = 168

Vậy \(x = 168\).

Bài 3. (1,5 điểm) Sắp đến hè, để giúp Nam tập luyện môn cầu lông, mẹ của Nam đã mua cho Nam một cây vợt cầu lông và một hộp cầu có \(20\) quả hết \(990\,000\) đồng (đã bao gồm thuế VAT). Trong đó, cây vợt có giá \(560\,000\) đồng (chưa có thuế VAT). Mẹ Nam mua ở siêu thị nên tất cả các mặt hàng người mua đều phải trả thêm thuế giá trị gia tăng VAT là \(10{\rm{\% }}\).

a) Tính giá tiền của cây vợt bao gồm thuế VAT mà mẹ của Nam đã mua.

b) Tính giá của mỗi quả cầu lông khi chưa tính thuế VAT.

Phương pháp

a) Tiền thuế VAT = 10%.giá trị sản phẩm.

Giá tiền của cây vợt sau khi đã tính thuế VAT là: giá ban đầu + thuế.

b) Số tiền phải trả cho hộp cầu có thuế VAT là: tổng số tiền – số tiền cây vợt sau khi đã tính thuế VAT.

Số tiền phải trả cho 1 quả cầu có thuế VAT là: số tiền hộp cầu có thuế VAT : 20 quả.

Số tiền mỗi quả cầu lông khi chưa tính thuế VAT là: số tiền có thuế : (1 + 10%).

Lời giải

a) Giá tiền của cây vợt sau khi đã tính thuế VAT là: \(560\;000 + 560\;000.\;10\%  = 616\;000\) (đồng)

Vậy giá tiền của cây vợt sau khi đã tính thuế VAT là 616 000 đồng.

b) Số tiền phải trả cho hộp cầu có thuế VAT là: \(990\;000 - 616\;000 = 374\;000\) (đồng)

Số tiền phải trả cho 1 quả cầu có thuế VAT là: \(374\;000:20 = 18\;700\) (đồng)

Giá của một quả cầu khi chưa tính thuế VAT là: \(18700:(1 + 10\% ) = 17000\) (đồng)

Vậy giá của một quả cầu khi chưa tính thuế VAT là 17 000 đồng.

Bài 4. (1,5 điểm) Một mảnh đất hình chữ nhật có chiều dài là 24m, chiều rộng 20m. Người ta chia mảnh đất thành hai khu, một khu trồng hoa và một khu trồng cỏ. Hoa sẽ trồng trong khu vực hình bình hành và cỏ trồng ở phần đất còn lại (như hình vẽ).

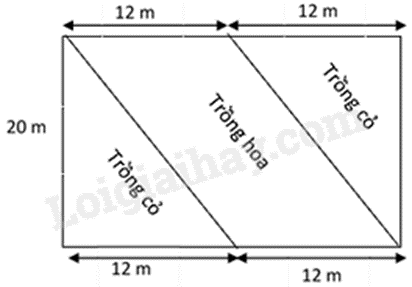
a) Tính diện tích mảnh đất hình chữ nhật.

b) Tính số tiền cần trả để trồng cỏ, biết giá mỗi mét vuông trồng cỏ là 40 000 đồng.

Phương pháp

a) Sử dụng công thức tính diện tích hình chữ nhật = chiều dài . chiều rộng.

b) Tính diện tích trồng hoa bằng công thức tính diện tích hình bình hành = chiều cao . đáy tương ứng.

Tính diện tích trồng cỏ = diện tích mảnh đất – diện tích trồng hoa.

Số tiền cần trả = giá mỗi mét vuông . diện tích trồng cỏ.

Lời giải

a) Diện tích mảnh đất là: 24.20 = 480 (\({m^2}\))

Vậy diện tích mảnh đất là 480\({m^2}\).

b) Diện tích đất dùng để trồng hoa là: 12.20 = 240 (\({m^2}\))

Diện tích đất dùng để trồng cỏ là: 480 – 240 = 240(\({m^2}\))

Tiền cần trả để trồng cỏ là: 240. 40 000 = 9 600 000 (đồng)

Vậy số tiền cần trả để trồng cỏ là 9 600 000 đồng.

Bài 5. (1,5 điểm) Cho đoạn thẳng \(AB = 9cm\). Lấy điểm \(C\) thuộc đoạn thẳng \(AB\) sao cho \(AC = 3cm\).

a) Tính độ dài đoạn thẳng \(BC\).

b) Lấy điểm \(M\) nằm giữa hai điểm \(C\) và \(B\) sao cho \(C\) là trung điểm của đoạn thẳng \(AM\). Tính \(AM\).

c) Lấy điểm \(O\) nằm ngoài đường thẳng \(AB\). Vẽ các đoạn thẳng \(OA,OB,OC\). Nêu tên các góc đỉnh \(O\) trên hình vẽ.

Phương pháp

a) Sử dụng kiến thức điểm nằm giữa hai điểm để tính CB theo AC và AB.

b) Sử dụng tính chất trung điểm để tính AM theo AC.

c) Quan sát hình vẽ để kể tên các góc.

Lời giải

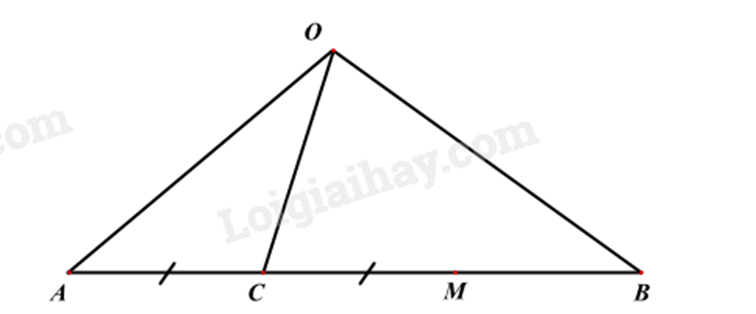
a) Vì điểm C thuộc đoạn thẳng AB nên ta có:

\(AC + CB = AB\)

\(3 + CB = 9\)

\(CB = 9 - 3 = 6\) (cm)

b) Vì điểm C là trung điểm của đoạn thẳng AM nên suy ra:

\(AM = 2AC\)

\(AM = 2.3 = 6\) (cm)

c) Các góc trong hình vẽ là: AOC; COB; AOB.