Đề ôn hè Toán 6 lên 7 - Đề 2

Đề bài

Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:

Câu 1: Tập hợp các ước nguyên của 4 là:

A. {0; -1; -2; -4}.

B. {1; 2; 4; -1; -2; -4}.

C. {1; 2; 4}.

D. {1; 2; 3; 4; -1; -2; -3; -4}.

Câu 2: Tổng các số nguyên \(x\) thoả mãn \( - 3 \le x < 2\) là:

A. -5.

B. -3.

C. 0.

D. -7.

Câu 3: Tính giá trị của biểu thức \(\left( { - 32} \right) + \left[ {3.\left( { - 5} \right) + 32} \right]\), ta được:

A. 15.

B. 49.

C. -79.

D. -15.

Câu 4: Một cửa hàng bán quần áo tháng thứ nhất lợi nhuận là -18 triệu đồng, tháng thứ hai lợi nhuận là 16 triệu đồng. Chủ cửa hàng muốn lợi nhuận sau ba tháng là 20 triệu đồng thì tháng thứ ba cửa hàng đó phải đạt lợi nhuận là:

A. 30 triệu đồng.

B. 18 triệu đồng.

C. 25 triệu đồng.

D. 22 triệu đồng.

Câu 5: Hình vuông có mấy trục đối xứng?

A. 1.

B. 2.

C. 3.

D. 4.

Câu 6: Các hình có tâm đối xứng là:

A. Hình a, b.

B. Hình b, d.

C. Hình b, c, d.

D. Hình a, d.

Câu 7: Bác An uốn một đoạn dây thép thành một móc treo đồ có dạng hình thang cân với độ dài đáy bé bằng 40 cm, đáy lớn là 50 cm, cạnh bên bằng 15 cm, móc treo có độ dài 10 cm. Hỏi bác An cần bao nhiêu mét dây thép?

A. 130 m.

B. 115 cm.

C. 1,3 m.

D. 13 m.

Câu 8: Trong ngày khai trương, một cửa hàng đồ uống đã thống kê số cốc bán được của bốn loại nước uống như sau:

Loại đồ uống cửa hàng bán được nhiều nhất trong ngày khai trương là:

A. Coco Matcha.

B. Matcha đá xay.

C. Trà kombucha.

D. Soda việt quất.

Câu 9: Làm tròn số 56,087 đến hàng phần trăm ta được

A. 56,09.

B. 56,08.

C. 56.

D. 56,1.

Câu 10: Tung hai đồng xu cân đối 50 lần, ta thu được kết quả như sau:

Xác suất thực nghiệm của sự kiện “Hai đồng xu đều sấp” là:

A. 0,22.

B. 0,4.

C. 0,44.

D. 0,16.

Câu 11: Cho bốn điểm A, B, C, D như hình vẽ:

Khi đó tia BC trùng với tia

A. BA.

B. CB.

C. CD.

D. BD.

Câu 12: Coi kim giờ và kim phút của một chiếc đồng hồ là hai tia chung gốc. Lúc 10 giờ, kim giờ và kim phút tạo với nhau một góc là

A. góc nhọn.

B. góc tù.

C. góc vuông.

D. góc bẹt.

Phần tự luận (7 điểm)

Bài 1. (2 điểm)

1. Thực hiện phép tính:

a) \(\left( { - 900} \right):\left\{ {150 - \left[ {{8^2} + 7.\left( { - 2} \right)} \right]} \right\} + {2025^0}\)

b) \(\frac{2}{3} + 25\% :\frac{3}{4}\)

2. Tìm x, biết:

a) \(3,14 + x = 8,34\)

b) \(\left( {x + \frac{1}{3}} \right):\frac{{12}}{{11}} = \frac{{11}}{9}\)

Bài 2. (1 điểm) Đắc Nhân Tâm được coi là cuốn sách của mọi thời đại, có ảnh hưởng sâu rộng và là hiện tượng đáng kinh ngạc trong ngành xuất bản Hoa Kỳ. Gần chín mươi năm kể từ khi ra đời, Đắc Nhân Tâm đã trở thành cuốn sách gối đầu giường của nhiều thế hệ, giúp người đọc hoàn thiện bản thân và đạt được cuộc sống thành công, hạnh phúc. Cuốn sách do Dale Carnegie (1888 – 1955) viết và đã được xuất bản lần đầu vào năm 1936 có độ dày 320 trang.

Bạn An đọc hết cuốn sách đó trong 3 ngày; ngày thứ nhất An đọc được \(\frac{3}{8}\) số trang của cuốn sách; ngày thứ hai An đọc được 40% số trang còn lại sau ngày thứ nhất.

a) Tính số trang sách An đọc được trong ngày thứ nhất, ngày thứ hai.

b) Tính tỉ số phần trăm của số trang sách còn lại sau hai ngày đọc so với số trang của cuốn sách.

Bài 3. (1 điểm) Biểu đồ tranh (hình vẽ bên) cho biết số lượng đồ chơi bán được tại cửa hàng của bố mẹ Bình vào ngày Chủ Nhật vừa qua.

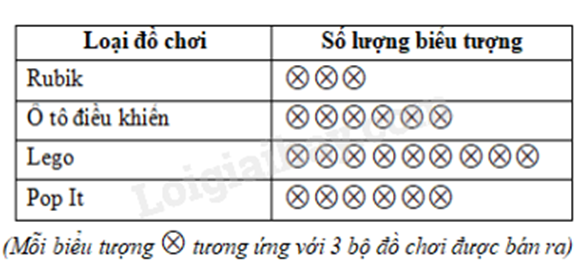
a) Loại đồ chơi nào được bố mẹ Bình bán ra nhiều nhất trong ngày Chủ Nhật đó là loại nào và số lượng là bao nhiêu bộ?

b) Lập bảng thống kê số đồ chơi bán được trong ngày Chủ Nhật của cửa hàng.

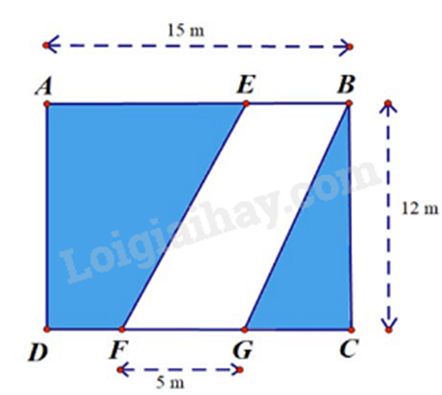
Bài 4. (1 điểm) Bác Nam có một mảng đất hình chữ nhật ABCD có chiều dài AB = 15 m, chiều rộng BC = 12 m. Người ta đã mở một con đường đi qua mảnh đất của bác, con đường có dạng hình bình hành BGFE có cạnh FG = 5m. Phần đất còn lại bác Nam dùng để trồng rau. Biết cứ \(5{m^2}\) đất thì cần 7 túi hạt giống, tính số túi hạt giống để gieo hết phần đất đó?

Bài 5. (1 điểm) Trên tia Ox lấy hai điểm A, B sao cho OA = 4cm, OB = 6cm. Lấy điểm C là trung điểm của đoạn thẳng OA.

a) Kể tên các đoạn thẳng có trên hình vẽ. Tính độ dài đoạn thẳng AB.

b) Điểm A có là trung điểm của đoạn thẳng CB không? Vì sao?

Bài 6. (1 điểm)

a) Tìm các số nguyên \(x\), sao cho: \(\left( {4x - 3} \right) \vdots \left( {x - 5} \right)\).

b) Để chuẩn bị cho hội diễn văn nghệ chào mừng lễ kỷ niệm 50 năm ngày Giải phóng miền Nam thống nhất đất nước của huyện, một trường THCS đã đăng kí tham gia tiết mục đồng ca hợp xướng. Dàn hợp xướng của trường ban đầu có 120 em học sinh. Nếu số học sinh nam tăng thêm 30 và số học sinh nữ giảm đi 10% thì số học sinh của dàn hợp xướng sẽ là 142 em. Hỏi ban đầu dàn hợp xướng có bao nhiêu em nam?

-------- Hết --------

Lời giải

Phần trắc nghiệm

Câu 1: Tập hợp các ước nguyên của 4 là:

A. {0; -1; -2; -4}.

B. {1; 2; 4; -1; -2; -4}.

C. {1; 2; 4}.

D. {1; 2; 3; 4; -1; -2; -3; -4}.

Phương pháp

Liệt kê các số tự nhiên mà 4 chia hết. Suy ra tập ước nguyên của 4.

Lời giải

Vì 4 chia hết cho 1, 2, 4 nên tập các ước nguyên của 4 là {1; 2; 4; -1; -2; -4}.

Đáp án: B.

Câu 2: Tổng các số nguyên \(x\) thoả mãn \( - 3 \le x < 2\) là:

A. -5.

B. -3.

C. 0.

D. -7.

Phương pháp

Liệt kê các số thoả mãn.

\( \le \): nhỏ hơn hoặc bằng.

\( < \): nhỏ hơn.

Lời giải

Các số \(x\) thoả mãn \( - 3 \le x < 2\) là: \(x \in \left\{ { - 3; - 2; - 1;0;1} \right\}\).

Tổng của các số \(x\) là: \(\left( { - 3} \right) + \left( { - 2} \right) + \left( { - 1} \right) + 0 + 1 =  - 5\).

Đáp án: A.

Câu 3: Tính giá trị của biểu thức \(\left( { - 32} \right) + \left[ {3.\left( { - 5} \right) + 32} \right]\), ta được:

A. 15.

B. 49.

C. -79.

D. -15.

Phương pháp

Sử dụng quy tắc dấu ngoặc để bỏ ngoặc, sử dụng tính chất của phép cộng.

Lời giải

\(\begin{array}{l}\left( { - 32} \right) + \left[ {3.\left( { - 5} \right) + 32} \right]\\ = \left( { - 32} \right) + \left[ {\left( { - 15} \right) + 32} \right]\\ = \left( { - 32} \right) + \left( { - 15} \right) + 32\\ = \left[ {\left( { - 32} \right) + 32} \right] + \left( { - 15} \right)\\ = 0 + \left( { - 15} \right)\\ =  - 15\end{array}\)

Đáp án: D.

Câu 4: Một cửa hàng bán quần áo tháng thứ nhất lợi nhuận là -18 triệu đồng, tháng thứ hai lợi nhuận là 16 triệu đồng. Chủ cửa hàng muốn lợi nhuận sau ba tháng là 20 triệu đồng thì tháng thứ ba cửa hàng đó phải đạt lợi nhuận là:

A. 30 triệu đồng.

B. 18 triệu đồng.

C. 25 triệu đồng.

D. 22 triệu đồng.

Phương pháp

Viết phép tính từ đề bài.

Tìm giá trị chưa biết của phép tính.

Lời giải

Giả sử \(x\) là lợi nhuận của tháng thứ ba.

Vì lợi nhuận sau ba tháng là 20 triệu đồng nên

\(\begin{array}{l}\left( { - 18} \right) + 16 + x = 20\\\left( { - 2} \right) + x = 20\\x = 20 + 2\\x = 22\end{array}\)

Vậy tháng thứ ba cửa hàng đó phải đạt lợi nhuận là 22 triệu đồng.

Đáp án: D.

Câu 5: Hình vuông có mấy trục đối xứng?

A. 1.

B. 2.

C. 3.

D. 4.

Phương pháp

Trục đối xứng là đường thẳng chia hình thành hai phần mà khi ta “gấp” hình theo đường thẳng đó thì hai phần “chồng khít” lên nhau.

Lời giải

Hình vuông có 4 trục đối xứng:

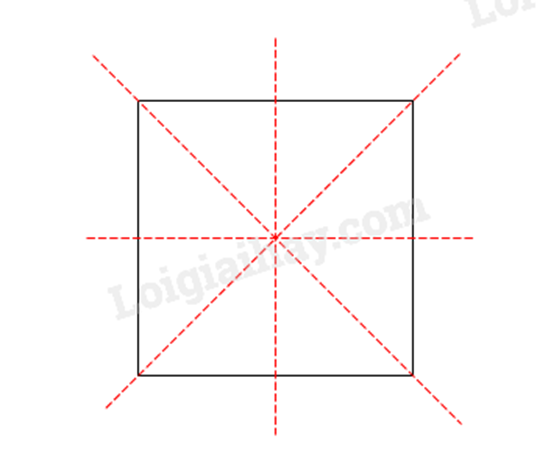
Đáp án: D.

Câu 6: Các hình có tâm đối xứng là:

A. Hình a, b.

B. Hình b, d.

C. Hình b, c, d.

D. Hình a, d.

Phương pháp

Tâm đối xứng là điểm sao cho khi quay nửa vòng quanh điểm điểm đó ta được vị trí mới của hình chồng khít với vị trí ban đầu (trước khi quay).

Lời giải

Hình a, d là hai hình có tâm đối xứng.

Đáp án: D.

Câu 7: Bác An uốn một đoạn dây thép thành một móc treo đồ có dạng hình thang cân với độ dài đáy bé bằng 40 cm, đáy lớn là 50 cm, cạnh bên bằng 15 cm, móc treo có độ dài 10 cm. Hỏi bác An cần bao nhiêu mét dây thép?

A. 130 m.

B. 115 cm.

C. 1,3 m.

D. 13 m.

Phương pháp

Số mét dây thép = chu vi hình thang cân + độ dài móc treo.

Lời giải

Chu vi hình thang cân là: 40 + 50 + 15.2 = 120 (cm)

Bác An cần số mét dây thép là: 120 + 10 = 130 (cm) = 1,3 m.

Đáp án: C.

Câu 8: Trong ngày khai trương, một cửa hàng đồ uống đã thống kê số cốc bán được của bốn loại nước uống như sau:

Loại đồ uống cửa hàng bán được nhiều nhất trong ngày khai trương là:

A. Coco Matcha.

B. Matcha đá xay.

C. Trà kombucha.

D. Soda việt quất.

Phương pháp

So sánh số cốc bán được.

Lời giải

Loại đồ uống cửa hàng bán được nhiều nhất trong ngày khai trương là Matcha đá xay (140 cốc).

Đáp án: B.

Câu 9: Làm tròn số 56,087 đến hàng phần trăm ta được

A. 56,09.

B. 56,08.

C. 56.

D. 56,1.

Phương pháp

Quy tắc làm tròn số:

- Đối với chữ số hàng làm tròn:

Giữ nguyên nếu chữ số ngay bên phải nhỏ hơn 5;

Tăng 1 đơn vị nếu chữ số ngay bên phải lớn hơn hay bằng 5.

- Đối với các chữ số sau hàng làm tròn:

Bỏ đi nếu ở phần thập phân,

Thay bởi các chữ số 0 nếu ở phần số nguyên.

Lời giải

Vì 7 > 5 nên số 56, 087 làm tròn đến hàng phần trăm được 56,09.

Đáp án: A.

Câu 10: Tung hai đồng xu cân đối 50 lần, ta thu được kết quả như sau:

Xác suất thực nghiệm của sự kiện “Hai đồng xu đều sấp” là:

A. 0,22.

B. 0,4.

C. 0,44.

D. 0,16.

Phương pháp

Xác suất thực nghiệm của sự kiện = Số lần sự kiện A xảy ra : Tổng số lần thực hiện hoạt động.

Lời giải

Xác suất thực nghiệm của sự kiện “Hai đồng xu đều sấp” là: \(\frac{{22}}{{50}} = 0,44\).

Đáp án: C.

Câu 11: Cho bốn điểm A, B, C, D như hình vẽ:

Khi đó tia BC trùng với tia

A. BA.

B. CB.

C. CD.

D. BD.

Phương pháp

Hai tia trùng nhau là hai tia chung gốc và cùng nằm 1 phía trên 1 đường thẳng.

Lời giải

Tia BC trùng với tia BD do cùng gốc C, hai điểm C, D nằm cùng một phía trên đường thẳng.

Đáp án: D.

Câu 12: Coi kim giờ và kim phút của một chiếc đồng hồ là hai tia chung gốc. Lúc 10 giờ, kim giờ và kim phút tạo với nhau một góc là

A. góc nhọn.

B. góc tù.

C. góc vuông.

D. góc bẹt.

Phương pháp

Góc nhọn là góc nhỏ hơn \(90^\circ \).

Góc tù là góc lớn hơn \(90^\circ \).

Góc vuông là góc \(90^\circ \).

Góc bẹt là góc \(180^\circ \).

Lời giải

Lúc 10 giờ, kim giờ và kim phút tạo với nhau một góc nhỏ hơn \(90^\circ \) nên là góc nhọn.

Đáp án: A.

Phần tự luận.

Bài 1. (2 điểm)

1. Thực hiện phép tính:

a) \(\left( { - 900} \right):\left\{ {150 - \left[ {{8^2} + 7.\left( { - 2} \right)} \right]} \right\} + {2025^0}\)

b) \(\frac{2}{3} + 25\% :\frac{3}{4}\)

2. Tìm x, biết:

a) \(3,14 + x = 8,34\)

b) \(\left( {x + \frac{1}{3}} \right):\frac{{12}}{{11}} = \frac{{11}}{9}\)

Phương pháp

1. Dựa vào quy tắc cộng, trừ, nhân chia số tự nhiên, phân số, thứ tự thực hiện phép tính để tính toán.

2. Sử dụng quy tắc chuyển vế để tìm x.

Lời giải

1.

a) \(\left( { - 900} \right):\left\{ {150 - \left[ {{8^2} + 7.\left( { - 2} \right)} \right]} \right\} + {2025^0}\)

\(\begin{array}{l} = \left( { - 900} \right):\left\{ {150 - \left[ {64 + \left( { - 14} \right)} \right]} \right\} + 1\\ = \left( { - 900} \right):\left\{ {150 - 50} \right\} + 1\\ = \left( { - 900} \right):100 + 1\\ = \left( { - 9} \right) + 1\\ =  - 8\end{array}\)

b) \(\frac{2}{3} + 25\% :\frac{3}{4}\)

\(\begin{array}{l} = \frac{2}{3} + \frac{1}{4}:\frac{3}{4}\\ = \frac{2}{3} + \frac{1}{4}.\frac{4}{3}\\ = \frac{2}{3} + \frac{1}{3}\\ = 1\end{array}\)

2. a) \(3,14 + x = 8,34\)

\(\begin{array}{l}x = 8,34 - 3,14\\x = 5,2\end{array}\)

Vậy \(x = 5,2\)

b) \(\left( {x + \frac{1}{3}} \right):\frac{{12}}{{11}} = \frac{{11}}{9}\)

\(\begin{array}{l}x + \frac{1}{3} = \frac{{11}}{9}.\frac{{12}}{{11}}\\x + \frac{1}{3} = \frac{4}{3}\\x = \frac{4}{3} - \frac{1}{3}\\x = 1\end{array}\)

Vậy \(x = 1\)

Bài 2. (1 điểm) Đắc Nhân Tâm được coi là cuốn sách của mọi thời đại, có ảnh hưởng sâu rộng và là hiện tượng đáng kinh ngạc trong ngành xuất bản Hoa Kỳ. Gần chín mươi năm kể từ khi ra đời, Đắc Nhân Tâm đã trở thành cuốn sách gối đầu giường của nhiều thế hệ, giúp người đọc hoàn thiện bản thân và đạt được cuộc sống thành công, hạnh phúc. Cuốn sách do Dale Carnegie (1888 – 1955) viết và đã được xuất bản lần đầu vào năm 1936 có độ dày 320 trang.

Bạn An đọc hết cuốn sách đó trong 3 ngày; ngày thứ nhất An đọc được \(\frac{3}{8}\) số trang của cuốn sách; ngày thứ hai An đọc được 40% số trang còn lại sau ngày thứ nhất.

a) Tính số trang sách An đọc được trong ngày thứ nhất, ngày thứ hai.

b) Tính tỉ số phần trăm của số trang sách còn lại sau hai ngày đọc so với số trang của cuốn sách.

Phương pháp

a) Tính \(\frac{m}{n}\) của \(a\), ta tính: \(a.\frac{m}{n}\).

Tính \(m\% \) của a, ta tính: \(a.m\% \).

b) Tỉ số phần trăm của a và b, ta tính: \(\frac{a}{b}.100\% \).

Lời giải

a) Số trang sách An đọc được trong ngày thứ nhất là: \(320.\frac{3}{8} = 120\) (trang)

Số trang sách còn lại sau ngày thứ nhất là: \(320 - 120 = 200\) (trang)

Số trang sách An đọc được trong ngày thứ hai là: \(200.40\%  = 80\) (trang)

b) Số trang sách còn lại sau hai ngày đọc là: 200 – 80 = 120 (trang)

Tỉ số phần trăm số trang sách còn lại sau hai ngày đọc so với số trang của cuốn sách là:

\(\frac{{120}}{{320}}.100\%  = 37,5\% \).

Bài 3. (1 điểm) Biểu đồ tranh (hình vẽ bên) cho biết số lượng đồ chơi bán được tại cửa hàng của bố mẹ Bình vào ngày Chủ Nhật vừa qua.

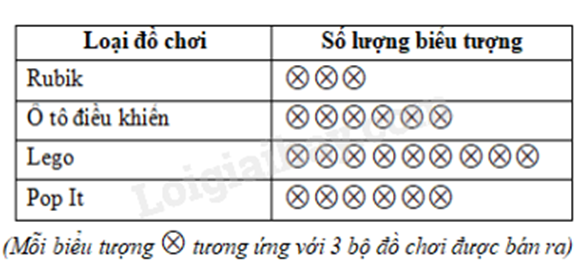
a) Loại đồ chơi nào được bố mẹ Bình bán ra nhiều nhất trong ngày Chủ Nhật đó là loại nào và số lượng là bao nhiêu bộ?

b) Lập bảng thống kê số đồ chơi bán được trong ngày Chủ Nhật của cửa hàng.

Phương pháp

a) Quan sát biểu đồ tranh, loại đồ chơi có số lượng biểu tượng nhiều nhất thì bán ra được nhiều nhất.

b) Tính số đồ chơi bán ra của từng loại = số biểu tượng . 3

Lời giải

a) Loại đồ chơi bố mẹ Bình bán ra nhiều nhất trong ngày Chủ Nhật đó là Lego.

Số lượng bán ra là: 9.3 = 27 (bộ)

b) Số lượng Rubik bán ra là: 3.3 = 9 (bộ)

Số lượng Ô tô điều khiển bán ra là: 6.3 = 18 (bộ)

Số lượng Pop It bán ra là: 6.3 = 18 (bộ)

Ta có bảng thống kê số đồ chơi bán ra được trong ngày Chủ Nhật của cửa hàng là:

Bài 4. (1 điểm) Bác Nam có một mảng đất hình chữ nhật ABCD có chiều dài AB = 15 m, chiều rộng BC = 12 m. Người ta đã mở một con đường đi qua mảnh đất của bác, con đường có dạng hình bình hành BGFE có cạnh FG = 5m. Phần đất còn lại bác Nam dùng để trồng rau. Biết cứ \(5{m^2}\) đất thì cần 7 túi hạt giống, tính số túi hạt giống để gieo hết phần đất đó?

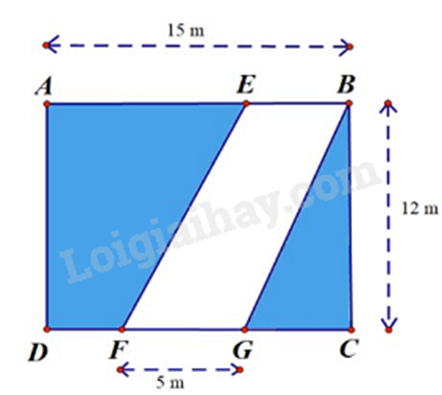
Phương pháp

- Tính diện tích mảnh đất: S_{hình chữ nhật} = chiều dài.chiều rộng.

- Tính diện tích con đường hình bình hành: S_{hình bình hành} = chiều cao.cạnh đáy tương ứng.

- Tính diện tích phần đất trồng rau = diện tích mảnh đất – diện tích con đường.

- Vì cứ \(5{m^2}\) đất thì cần 7 túi hạt giống nên số túi hạt giống cần để gieo hết phần đất bằng:

diện tích phần đất : 5 . 7

Lời giải

Diện tích mảnh đất hình chữ nhật ABCD là: \(15.12 = 180\left( {{m^2}} \right)\)

Diện tích con đường hình bình hành BGFE là: \(12.5 = 60\left( {{m^2}} \right)\)

Diện tích phần đất bác Nam trồng rau là: \(180 - 60 = 120\left( {{m^2}} \right)\)

Vì cứ \(5{m^2}\) đất thì cần 7 túi hạt giống nên số túi hạt giống cần là: \(120:5.7 = 168\) (túi)

Vậy số túi hạt giống để gieo hết phần đất đó là 168 túi.

Bài 5. (1 điểm) Trên tia Ox lấy hai điểm A, B sao cho OA = 4cm, OB = 6cm. Lấy điểm C là trung điểm của đoạn thẳng OA.

a) Kể tên các đoạn thẳng có trên hình vẽ. Tính độ dài đoạn thẳng AB.

b) Điểm A có là trung điểm của đoạn thẳng CB không? Vì sao?

Phương pháp

a) Quan sát các đoạn thẳng trên hình vẽ.

Tính độ dài đoạn thẳng AB dựa vào đoạn thẳng OA và OB.

b) Trung điểm của đoạn thẳng là điểm nằm giữa hai đầu mút và chia đoạn thẳng thành hai phần bằng nhau.

Lời giải

Vẽ hình:

- Vẽ tia Ox.

- Đo đoạn thẳng 4cm trên tia Ox từ điểm O để lấy điểm A.

- Đo đoạn thẳng 6cm trên tia Ox từ điểm O để lấy điểm B.

- Lấy điểm C nằm giữa O và A, độ dài OC bằng một nửa OA.

Ta được hình vẽ.

a) Các đoạn thẳng có trên hình vẽ là: OC, OA, OB, CA, CB, AB.

Vì điểm A nằm giữa hai điểm O và B nên OA + AB = OB.

Thay OA = 4cm, OB = 6cm, ta được:

4 + AB = 6

AB = 6 – 4

AB = 2

Vậy AB = 2cm.

b) Vì điểm C là trung điểm của đoạn thẳng OA nên OC = CA.

\(OC = CA = \frac{1}{2}OA = \frac{1}{2}.4 = 2\left( {cm} \right)\)

Vì điểm A nằm giữa hai điểm C và B, AC = AB = 2cm nên A là trung điểm của đoạn CB.

Bài 6. (1 điểm)

a) Tìm các số nguyên \(x\), sao cho: \(\left( {4x - 3} \right) \vdots \left( {x - 5} \right)\).

b) Để chuẩn bị cho hội diễn văn nghệ chào mừng lễ kỷ niệm 50 năm ngày Giải phóng miền Nam thống nhất đất nước của huyện, một trường THCS đã đăng kí tham gia tiết mục đồng ca hợp xướng. Dàn hợp xướng của trường ban đầu có 120 em học sinh. Nếu số học sinh nam tăng thêm 30 và số học sinh nữ giảm đi 10% thì số học sinh của dàn hợp xướng sẽ là 142 em. Hỏi ban đầu dàn hợp xướng có bao nhiêu em nam?

Phương pháp

a) Đưa \(\left( {4x - 3} \right)\) về tổng hai số chia hết cho \(\left( {x - 5} \right)\). Từ đó \(\left( {x - 5} \right)\) là ước của một số.

Lập bảng giá trị để tìm x.

b) Tính tổng số học sinh sau khi tăng số học sinh nam.

Vì sau khi giảm 10% học sinh nữ thì còn lại 142 em nên ta tính được 10% ứng với bao nhiêu số học sinh nữ.

Từ đó tính số học sinh nữ của dàn hợp xướng.

Số học sinh nam bằng tổng số học sinh – số học sinh nữ.

Lời giải

a) Ta có: \(\left( {4x - 3} \right) \vdots \left( {x - 5} \right)\)

               \(\begin{array}{l}\left( {4x - 20 + 20 - 3} \right) \vdots \left( {x - 5} \right)\\\left[ {4\left( {x - 5} \right) + 17} \right] \vdots \left( {x - 5} \right)\end{array}\)

Mà \(4\left( {x - 5} \right) \vdots \left( {x - 5} \right)\) nên \(17 \vdots \left( {x - 5} \right)\)

Do đó \(\left( {x - 5} \right) \in \)Ư(17) \( = \left\{ { - 1;1; - 17;17} \right\}\).

Ta có bảng giá trị sau:

Vậy \(x \in \left\{ {4;6; - 12;22} \right\}\).

b) Nếu số học sinh nam tăng thêm 30 thì dàn hợp xướng có:

\(120 + 30 = 150\) (học sinh)

Để tổng số học sinh chỉ còn 142 học sinh thì số học sinh nữ phải giảm đi:

\(150 - 142 = 8\) (học sinh)

Như vậy, 10% số học sinh nữ là 8 em. Do đó số học sinh nữ là: \(8:10\%  = 80\) (học sinh)

Số học sinh nam ban đầu là: \(120 - 80 = 40\) học sinh.