Đề ôn hè Toán 6 lên 7 - Đề 3

Đề bài

Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:

Câu 1: Cho M là tập hợp các số tự nhiên nhỏ hơn 5. Cách viết tập hợp M đúng là:

A. \(M = \left\{ {1;2;3;4} \right\}\).

B. \(M = \left\{ {1;2;3;4;5} \right\}\).

C. \(M = \left\{ {0;1;2;3;4} \right\}\).

D. \(M = \left\{ {0;1;2;3;4;5} \right\}\).

Câu 2: Trong các số sau, số nào là số nguyên tố?

A. 10.

B. 29.

C. 1.

D. 15.

Câu 3: Quan sát các biển báo giao thông dưới đây:

Biển báo có dạng chữ nhật là

A. Biển báo 1.

B. Biển báo 2.

C. Biển báo 3.

D. Cả A, B, C đều đúng.

Câu 4: Trong các số \(125;\;1818;\;2430;\;7857.\) Số chia hết cho cả 5 và 9 là:

A. \(125\).

B. \(1818\).

C. \(2430.\)

D. \(7857.\)

Câu 5: Thân nhiệt của bệnh nhân A trong 10 tiếng theo dõi được ghi lại trong bảng sau:

Hãy cho biết dữ liệu nào không hợp lí?

A. 37,5.

B. 40.

C. 0.

D. 36,5.

Câu 6: Biểu đồ tranh dưới đây cho biết số lượng sách học sinh đọc sách tại thư viện trong một ngày như sau:

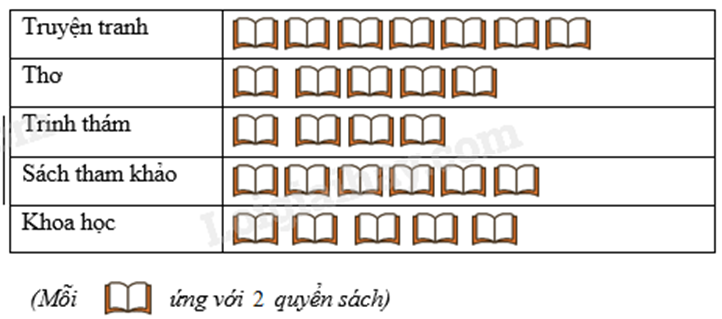
Tổng số quyển sách học sinh đọc tại thư viện trong một ngày là:

A. 27.

B. 54.

C. 81.

D. 104.

Câu 7: Kết quả của phép tính \(\frac{3}{8} - \frac{4}{5}\) là:

A. \(\frac{{ - 17}}{{40}}\).

B. \(\frac{{ - 47}}{{40}}\).

C. \(\frac{{47}}{{40}}\).

D. \(\frac{{17}}{{40}}\).

Câu 8: Giá trị phân số \(\;\frac{{ - 4}}{7}\) của số \(56\) là

A. -112.

B. -2.

C. -224.

D. -32.

Câu 9: Cho đoạn thẳng \({\rm{AP}}\) có độ dài bằng \(12{\rm{cm}}\). Nếu \({\rm{F}}\) là trung điểm của \({\rm{AP}}\) thì

A. \({\rm{FP}} = 6{\rm{cm}}\).

B. \({\rm{AF}} = 12{\rm{cm}}\).

C. \({\rm{AF}} < {\rm{FP}}\).

D. \({\rm{FP}} = 24{\rm{cm}}\).

Câu 10: Số đo của góc \(\widehat {cOd}\) trong hình dưới đây là:

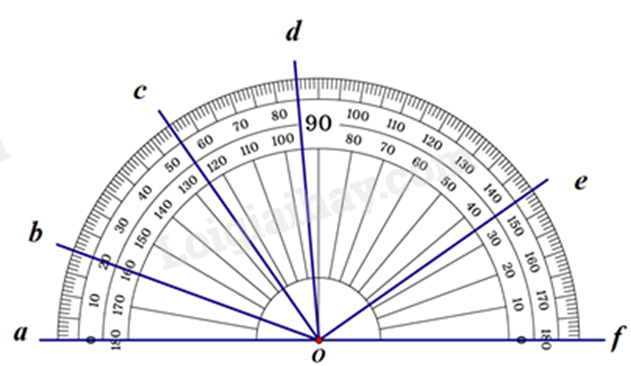
A. \(55^\circ \).

B. \(95^\circ \).

C. \(85^\circ \).

D. \(30^\circ \).

Câu 11: Cho hình vẽ sau:

Hai tia đối nhau trên hình là:

A. Tia AC và AD.

B. Tia CD và DA.

C. Tia DA và DB.

D. Tia BD và CD.

Câu 12: Số trục đối xứng của hình ngôi sao dưới đây là

A. 2.

B. 3.

C. 4.

D. 5.

Phần tự luận (7 điểm)

Bài 1. (1,5 điểm) Thực hiện phép tính:

a) \(50 - \left[ {\left( {20 - {2^3}} \right):2 + 34} \right]\)

b) \(\frac{8}{{50}} - \frac{3}{{75}} + \frac{1}{4}\)

c) \(0,7.2\frac{2}{3}.20.0,375.\frac{5}{{28}}\)

Bài 2. (1 điểm) Tìm \(x\), biết:

a) \(\frac{x}{7} = \frac{{12}}{{21}}\).

b) \(\frac{4}{7} + \frac{5}{{28}}:x = \frac{1}{{14}}\).

Bài 3. (1 điểm) Một quán trà trái cây cuối ngày bán còn lại \(3\) loại trà sau:  \(\frac{9}{7}\) lít trà ổi, lượng trà đào ít hơn trà ổi là  \(\frac{2}{7}\) lít, trà dâu ít hơn trà ổi là \(\frac{1}{2}\) lít. Giá bán của mỗi loại trà trên được cho trong bảng sau:

Một người muốn mua hết lượng trà trên để tổ chức tiệc, hỏi người đó cần bao nhiêu tiền? Biết nếu mua hết lượng trà trên, quán sẽ giảm giá \(\frac{1}{{10}}\) tổng số tiền cho người mua.

Bài 4. (1 điểm) Một khoảng sân có dạng hình chữ nhật với chiều dài 12m và chiều rộng 7m. Người ta để một phần của sân để trồng hoa (phần kẻ sọc), phần còn lại lát gạch (phần trắng).

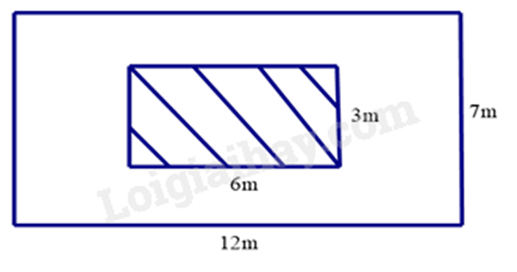
a) Tính chu vi của khoảng sân và diện tích phần còn lại để lát gạch?

b) Nếu lát phần sân còn lại bằng những viên gạch hình vuông cạnh 50cm thì cần bao nhiêu viên gạch? Số tiền lát gạch là bao nhiêu? Biết 1 viên gạch giá 55 000 đồng.

Bài 5. (2,5 điểm)

1. Cho đoạn thẳng \({\rm{HK}} = 4{\rm{cm}}\). Trên tia \({\rm{HK}}\) lấy điểm \({\rm{P}}\) sao cho \({\rm{HP}} = 2{\rm{cm}}\).

a) Tính độ dài đoạn thẳng \({\rm{KP}}\).

b) Điểm \({\rm{P}}\) có là trung điểm của đoạn thẳng \({\rm{HK}}\) không?  Vì sao?

2.

a) Vẽ đường thẳng \({\rm{MN}}\) cắt đường thẳng \({\rm{EF}}\) tại điểm \({\rm{I}}\) sao cho góc \({\rm{EIN}}\) bằng \(30^\circ \). Góc \({\rm{EIN}}\) là góc gì? Giải thích.

b) Góc MIN có số đo gấp bao nhiêu lần số đo góc \({\rm{EIN}}\).

-------- Hết --------

Lời giải

Phần trắc nghiệm

Câu 1: Cho M là tập hợp các số tự nhiên nhỏ hơn 5. Cách viết tập hợp M đúng là:

A. \(M = \left\{ {1;2;3;4} \right\}\).

B. \(M = \left\{ {1;2;3;4;5} \right\}\).

C. \(M = \left\{ {0;1;2;3;4} \right\}\).

D. \(M = \left\{ {0;1;2;3;4;5} \right\}\).

Phương pháp

Xác định các số tự nhiên nhỏ hơn 5.

Sử dụng kiến thức viết tập hợp bằng cách liệt kê.

Lời giải

Tập hợp các số tự nhiên nhỏ hơn 5 là \(M = \left\{ {0;1;2;3;4} \right\}\)

Đáp án: C.

Câu 2: Trong các số sau, số nào là số nguyên tố?

A. 10.

B. 29.

C. 1.

D. 15.

Phương pháp

Dựa vào kiến thức về số nguyên tố: Số nguyên tố là số chỉ có hai ước nguyên dương là 1 và chính nó.

Lời giải

Trong các số trên, số nguyên tố là 29.

Đáp án: B.

Câu 3: Quan sát các biển báo giao thông dưới đây: 

Biển báo có dạng chữ nhật là

A. Biển báo 1.

B. Biển báo 2.

C. Biển báo 3.

D. Cả A, B, C đều đúng.

Phương pháp

Dựa vào hình dạng của các hình phẳng.

Lời giải

Biển báo 1 có dạng hình tam giác đều.

Biển báo 2 có dạng hình vuông.

Biển báo 3 có dạng hình chữ nhật.

Đáp án: C.

Câu 4: Trong các số \(125;\;1818;\;2430;\;7857.\) Số chia hết cho cả 5 và 9 là:

A. \(125\).

B. \(1818\).

C. \(2430.\)

D. \(7857.\)

Phương pháp

Các số chia hết cho 5 có chữ số tận cùng là 0 hoặc 5.

Các số chia hết cho 9 thì tổng các chữ số của số đó chia hết cho 9.

Lời giải

Trong các số trên, có 2 số chia hết cho 5, đó là: 125; 2430.

Ta có:

1 + 2 + 5 = 8 nên 125 không chia hết cho 9.

2 + 4 + 3 + 0 = 9 nên 2430 chia hết cho 9.

Đáp án: C.

Câu 5: Thân nhiệt của bệnh nhân A trong 10 tiếng theo dõi được ghi lại trong bảng sau:

Hãy cho biết dữ liệu nào không hợp lí?

A. 37,5.

B. 40.

C. 0.

D. 36,5.

Phương pháp

Dựa vào kiến thức về nhiệt độ của người.

Lời giải

Dữ liệu không hợp lí là 0.

Đáp án: C.

Câu 6: Biểu đồ tranh dưới đây cho biết số lượng sách học sinh đọc sách tại thư viện trong một ngày như sau:

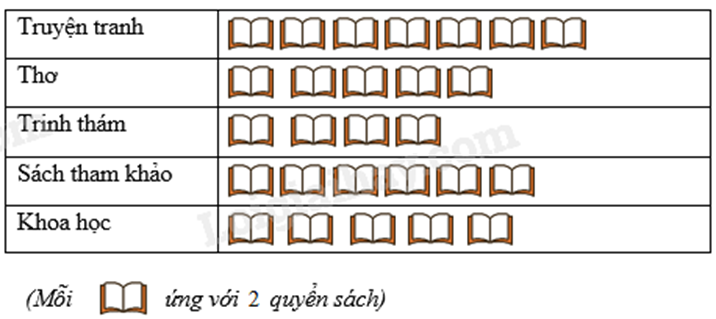
Tổng số quyển sách học sinh đọc tại thư viện trong một ngày là:

A. 27.

B. 54.

C. 81.

D. 104.

Phương pháp

Tính tổng số biểu tượng.

Mỗi biểu tượng ứng với 2 quyển sách nên ta tính được số quyển sách.

Lời giải

Tổng số biểu tượng trong biểu đồ tranh là:

7 + 5 + 4 + 6 + 5 = 27 (biểu tượng)

Tổng số quyển sách học sinh đọc tại thư viện trong một ngày là:

\(27.2 = 54\) (quyển)

Đáp án: B.

Câu 7: Kết quả của phép tính \(\frac{3}{8} - \frac{4}{5}\) là:

A. \(\frac{{ - 17}}{{40}}\).

B. \(\frac{{ - 47}}{{40}}\).

C. \(\frac{{47}}{{40}}\).

D. \(\frac{{17}}{{40}}\).

Phương pháp

Thực hiện trừ hai phân số khác mẫu.

Lời giải

Ta có: \(\frac{3}{8} - \frac{4}{5} = \frac{{15}}{{40}} - \frac{{32}}{{40}} = \frac{{ - 17}}{{40}}\).

Đáp án: A.

Câu 8: Giá trị phân số \(\;\frac{{ - 4}}{7}\) của số \(56\) là

A. -112.

B. -2.

C. -224.

D. -32.

Phương pháp

Tính giá trị \(\frac{m}{n}\) của một số a, ta tính: \(a.\frac{m}{n}\).

Lời giải

Giá trị phân số \(\;\frac{{ - 4}}{7}\) của số \(56\) là: \(56.\frac{{ - 4}}{7} =  - 32\).

Đáp án: D.

Câu 9: Cho đoạn thẳng \({\rm{AP}}\) có độ dài bằng \(12{\rm{cm}}\). Nếu \({\rm{F}}\) là trung điểm của \({\rm{AP}}\) thì

A. \({\rm{FP}} = 6{\rm{cm}}\).

B. \({\rm{AF}} = 12{\rm{cm}}\).

C. \({\rm{AF}} < {\rm{FP}}\).

D. \({\rm{FP}} = 24{\rm{cm}}\).

Phương pháp

Trung điểm của một đoạn thẳng chia đoạn thẳng đó thành hai phần có độ dài bằng nhau và bằng một nửa độ dài đoạn thẳng.

Lời giải

Vì F là trung điểm của AP nên \(AF = FP = \frac{{AP}}{2} = \frac{{12}}{2} = 6\left( {cm} \right)\).

Đáp án: A.

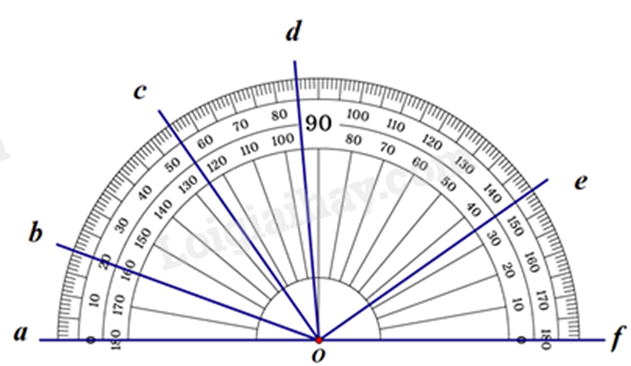
Câu 10: Số đo của góc \(\widehat {cOd}\) trong hình dưới đây là:

A. \(55^\circ \).

B. \(95^\circ \).

C. \(85^\circ \).

D. \(30^\circ \).

Phương pháp

Xác định vị trị các tia.

Trừ góc để tính \(\widehat {cOd}\).

Lời giải

Quan sát hình vẽ, ta thấy: \(\widehat {aOc} = 55^\circ ;\widehat {aOd} = 85^\circ \)

Vì tia Oc nằm giữa tia OA và tia Od nên ta có: \(\widehat {aOc} + \widehat {cOd} = \widehat {aOd}\)

Suy ra \(\widehat {cOd} = \widehat {aOd} - \widehat {aOc} = 85^\circ  - 55^\circ  = 30^\circ \).

Đáp án: D.

Câu 11: Cho hình vẽ sau:

Hai tia đối nhau trên hình là:

A. Tia AC và AD.

B. Tia CD và DA.

C. Tia DA và DB.

D. Tia BD và CD.

Phương pháp

Kiểm tra các đáp án.

Hai tia đối nhau là hai tia chung gốc và nằm khác phía trên 1 đường thẳng.

Lời giải

Vì C và D nằm cùng phía so với A nên tia AC và AD không phải hai tia đối nhau.

Vì A và B nằm khác phía so với điểm D nên tia DA và DB là hai tia đối nhau.

Tia CD và DA; tia BD và CD không cùng gốc nên không thể là hai tia đối nhau.

Đáp án: C.

Câu 12: Số trục đối xứng của hình ngôi sao dưới đây là

A. 2.

B. 3.

C. 4.

D. 5.

Phương pháp

Trục đối xứng là đường thẳng chia hình thành hai phần mà khi ta “gấp” hình theo đường thẳng đó thì hai phần “chồng khít” lên nhau.

Lời giải

Hình ngôi sao có 5 trục đối xứng.

Đáp án: D.

Phần tự luận.

Bài 1. (1,5 điểm) Thực hiện phép tính:

a) \(50 - \left[ {\left( {20 - {2^3}} \right):2 + 34} \right]\).

b) \(\frac{8}{{50}} - \frac{3}{{75}} + \frac{1}{4}\).

c) \(0,7.2\frac{2}{3}.20.0,375.\frac{5}{{28}}\).

Phương pháp

a) Thực hiện tính luỹ thừa, tính phép tính trong ( ) \( \to \) [ ].

b) Rút gọn các phân số về phân số tối giản, thực hiện tính một cách hợp lí.

c) Đưa hỗn số về phân số để thực hiện phép nhân phân số.

Lời giải

a) \( = 50 - \left[ {\left( {20 - 8} \right):2 + 34} \right]\)

\( = 50 - \left[ {12:2 + 34} \right]\)

\( = 50 - \left[ {6 + 34} \right]\)

\( = 50 - 40 = 10\)

b) \(\frac{8}{{50}} - \frac{3}{{75}} + \frac{1}{4}\)

\( = \frac{4}{{25}} - \frac{1}{{25}} + \frac{1}{4} = \frac{3}{{25}} + \frac{1}{4} = \frac{{12 + 25}}{{100}} = \frac{{37}}{{100}}\)

c) \(0,7\,\,.\,\,2\frac{2}{3}\,\,.\,\,20\,\,.\,\,0,375\,\,.\,\,\frac{5}{{28}} = \frac{7}{{10}}\,\,.\,\,\frac{5}{{28}}\,\,.\,\,20\,\,.\,\,2\frac{2}{3}\,\,.\,\,\frac{{15}}{4}\)

\(\, = \frac{1}{8}\,\,.\,\,20\,\,.\,\,\frac{8}{3}\,\,.\,\,\frac{{15}}{4} = \left( {\frac{1}{8}\,\,.\,\,\frac{8}{3}} \right)\,\,.\,\,\left( {\frac{{15}}{4}\,\,.\,\,20} \right) = \frac{1}{3}\,\,.\,\,75 = 25\)

Bài 2. (1 điểm) Tìm \(x\), biết:

a) \(\frac{x}{7} = \frac{{12}}{{21}}\).

b) \(\frac{4}{7} + \frac{5}{{28}}:x = \frac{1}{{14}}\).

Phương pháp

a) \(\frac{a}{b} = \frac{c}{d}\) thì \(a = \frac{c}{d}.b\).

b) Sử dụng quy tắc chuyển vế để tìm x.

Lời giải

a) \(\frac{x}{7} = \frac{{12}}{{21}}\)

\(x = \frac{{12}}{{21}}.7\)

\(x = 4\)

Vậy \(x = 4\)

b) \(\frac{4}{7} + \frac{5}{{28}}:x = \frac{1}{{14}}\)

\(\begin{array}{l}\frac{5}{{28}}:x = \frac{1}{{14}} - \frac{4}{7}\\\frac{5}{{28}}:x = \frac{{ - 1}}{2}\end{array}\)

\(\begin{array}{l}x = \frac{5}{{28}}:\left( {\frac{{ - 1}}{2}} \right)\\x = \frac{{ - 5}}{{14}}\end{array}\)

Vậy \(x = \frac{{ - 5}}{{14}}\)

Bài 3. (1 điểm) Một quán trà trái cây cuối ngày bán còn lại \(3\) loại trà sau:  \(\frac{9}{7}\) lít trà ổi, lượng trà đào ít hơn trà ổi là  \(\frac{2}{7}\) lít, trà dâu ít hơn trà ổi là \(\frac{1}{2}\) lít. Giá bán của mỗi loại trà trên được cho trong bảng sau:

Một người muốn mua hết lượng trà trên để tổ chức tiệc, hỏi người đó cần bao nhiêu tiền? Biết nếu mua hết lượng trà trên, quán sẽ giảm giá \(\frac{1}{{10}}\) tổng số tiền cho người mua.

Phương pháp

Tính số lít trà đào, trà dâu còn lại theo số lít trà ổi.

Tính số tiền mua trà khi chưa giảm giá:

Giá tiền mua một loại trà = số lít . giá tiền (đồng/lít).

Tính số tiền mua trà sau khi giảm giá:

Số tiền mua trà khi chưa giảm giá - \(\frac{1}{{10}}\). Số tiền mua trà khi chưa giảm giá.

Lời giải

Số lít trà đào còn lại là:

\(\frac{9}{7} - \frac{2}{7} = 1\) (lít)

Số lít trà dâu còn lại là:

\(\frac{9}{7} - \frac{1}{2} = \frac{{11}}{{14}}\) (lít)

Số tiền để mua hết số trà khi chưa giảm giá là:

\(\frac{9}{7} \cdot 56000 + 1 \cdot 50000 + \frac{{11}}{{14}} \cdot 56000 = 166000\) (đồng)

Số tiền để mua hết số trà sau khi giảm giá là:

\(166000 - \frac{1}{{10}} \cdot 166000 = 149400\) (đồng)

Vậy người đó cần 149 400 đồng để mua hết lượng trà trên.

Bài 4. (1 điểm) Một khoảng sân có dạng hình chữ nhật với chiều dài 12m và chiều rộng 7m. Người ta để một phần của sân để trồng hoa (phần kẻ sọc), phần còn lại lát gạch (phần trắng).

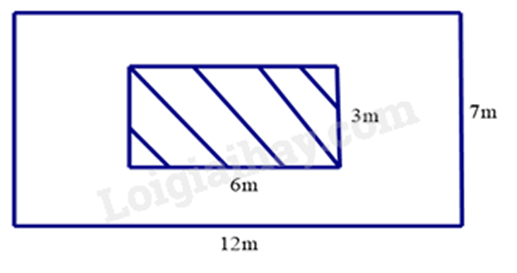
a) Tính chu vi của khoảng sân và diện tích phần còn lại để lát gạch?

b) Nếu lát phần sân còn lại bằng những viên gạch hình vuông cạnh 50cm thì cần bao nhiêu viên gạch? Số tiền lát gạch là bao nhiêu? Biết 1 viên gạch giá 55 000 đồng.

Phương pháp

a) Sử dụng công thức tính chu vi, diện tích hình chữ nhật:

Chu vi = (chiều dài + chiều rộng) . 2

Diện tích = chiều dài. chiều rộng.

Diện tích phần lát gạch = diện tích sân – diện tích phần trồng hoa.

b) Tính diện tích viên gạch hình vuông = cạnh . cạnh.

Số viên gạch cần lát = diện tích phần lát gạch : diện tích một viên gạch.

Số tiền lát gạch = số viên gạch . giá một viên gạch.

Lời giải

a) Chu vi khoảng sân là: \(\left( {12 + 7} \right).2 = 38\left( m \right)\)

Diện tích phần lát gạch là: \(12.7 - 6.3 = 66\left( {{m^2}} \right)\)

Vậy chu vi của khoảng sân là 38m; diện tích của phần lát gạch là \(66{m^2}\).

b) Diện tích 1 viên gạch là: \(0,5.0,5 = 0,25\left( {{m^2}} \right)\)

Số viên gạch cần lát là: \(66:0,25 = 264\) (viên)

Số tiền lát gạch là: \(264.55{\rm{ }}000 = 14{\rm{ }}520{\rm{ }}000\)(đồng).

Vậy cần 264 viên gạch và số tiền lát gạch là 14 520 000 đồng.

Bài 5. (2,5 điểm)

1. Cho đoạn thẳng \({\rm{HK}} = 4{\rm{cm}}\). Trên tia \({\rm{HK}}\) lấy điểm \({\rm{P}}\) sao cho \({\rm{HP}} = 2{\rm{cm}}\).

a) Tính độ dài đoạn thẳng \({\rm{KP}}\).

b) Điểm \({\rm{P}}\) có là trung điểm của đoạn thẳng \({\rm{HK}}\) không?  Vì sao?

2.

a) Vẽ đường thẳng \({\rm{MN}}\) cắt đường thẳng \({\rm{EF}}\) tại điểm \({\rm{I}}\) sao cho góc \({\rm{EIN}}\) bằng \(30^\circ \). Góc \({\rm{EIN}}\) là góc gì? Giải thích.

b) Góc MIN có số đo gấp bao nhiêu lần số đo góc \({\rm{EIN}}\).

Phương pháp

1.

a) Dựa vào kiến thức về điểm nằm giữa hai điểm để tính độ dài đoạn thẳng.

b) Kiểm tra trung điểm của đoạn thẳng: Điểm P là trung điểm của đoạn thẳng HK nếu P nằm giữa H và K và PH = PK.

2.

a) Vẽ đường thẳng thoả mãn điều kiện.

Xác định loại góc:

+ Nếu góc lớn hơn \(0^\circ \) và nhỏ hơn \(90^\circ \) thì là góc nhọn.

+ Nếu góc bằng \(90^\circ \) thì là góc vuông.

+ Nếu góc lớn hơn \(90^\circ \) và nhỏ hơn \(180^\circ \) thì là góc tù.

+ Nếu góc bằng \(180^\circ \) thì là góc bẹt.

b) Tính tỉ số giữa số đo góc MIN với góc EIN.

Lời giải

1.

a) Vì \({\rm{P}}\) nằm giữa hai điểm \({\rm{H}}\) và \({\rm{K}}\) nên \({\rm{HP}} + {\rm{KP}} = {\rm{HK}}\).

Suy ra \({\rm{KP}} = {\rm{HK}} - {\rm{HP}} = 4 - 2 = 2{\rm{cm}}\).

b) Điểm \({\rm{P}}\) là trung điểm của đoạn thẳng \({\rm{HK}}\) vì điểm \({\rm{P}}\) nằm giữa hai điểm \({\rm{H}}\), \({\rm{K}}\) và \({\rm{HP}} = {\rm{KP}} = 2{\rm{cm}}.\)

2.

a)

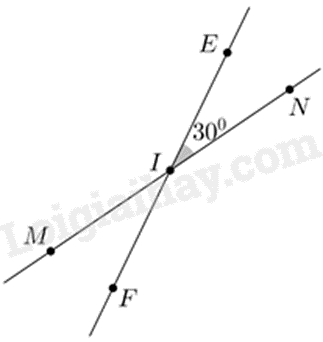
Góc \({\rm{EIN}}\) là góc nhọn vì \(\widehat {{\rm{EIN\;}}} = 30^\circ  < 90^\circ \).

b) Vì I thuộc đoạn thẳng MN nên góc \(MIN\) là góc bẹt, do đó \(\widehat {{\rm{MIN\;}}} = 180^\circ \).

Số đo góc \(MIN\) gấp số đo góc EIN số lần là: \(\;\frac{{180^\circ }}{{30^\circ }} = 3\) (lần).

Vậy góc MIN có số đo gấp 3 lần số đo góc \({\rm{EIN}}\).