Dạng 1. Viết tập hợp Chủ đề 1 Ôn hè Toán 6

Lý thuyết

Một tập hợp (gọi tắt là tập) bao gồm những đối tượng nhất định, những đối tượng đó được gọi là những phần tử của tập hợp mà ta nhắc đến.

Phần tử x thuộc tập hợp A được kí hiệu là \(x \in A\), y không thuộc tập hợp A được kí hiệu là \(y \notin A\)

Ta thường viết tập hợp theo 2 cách:

Cách 1: Liệt kê các phần tử của tập hợp

+ Các phần tử của một tập hợp được viết trong hai dấu ngoặc nhọn { }, ngăn cách nhau bởi dấu  “ ; ”

+ Mỗi phần tử được liệt kê một lần , thứ tự liệt kê tùy ý.

Cách 2: Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp đó

Bài tập

Bài 1: Theo Âm Lịch, năm 2024 là năm Giáp Thìn, tức năm con Rồng – xếp thứ năm trong 12 con giáp. Năm Giáp Thìn sẽ bắt đầu từ ngày 10/02/2024 và kết thúc năm vào ngày 28/01/2025 theo lịch dương. Gọi A là tập hợp các chữ số xuất hiện ở hình bên. Khi đó

A. \(A = \left\{ {4;2;0;2} \right\}\).

B. \(A = \left\{ {2;0;2;4} \right\}\).

C. \(A = \left\{ {0;2;4} \right\}\).

D. \(A = \left\{ {0;2} \right\}\).

Bài 2: Viết tập hợp sau bằng cách liệt kê các phần tử \(A = \left\{ {\left. {x \in {\mathbb{N}^*}} \right|2021 < x \le 2023} \right\}\)

A. \(A = \left\{ {2022,{\mkern 1mu} 2023} \right\}\).

B. \(A = \left\{ {2022} \right\}\).

C. \(A = \left\{ {2022;{\mkern 1mu} 2023} \right\}\).

D. \(A = \left\{ {2023} \right\}\).

Bài 3: Cho tập hợp E gồm các chữ cái trong từ “TOÁN HỌC”. Cách viết nào đúng?

A. E = {T; A; N; H; O; C}.

B. E = [T; O; A; N; H; C].

C. E = (T; O; A; N; H; C).

D. E = {T; O; A; N; H; O; C}.

Bài 4: Cho tập hợp \(\left\{ {x \in {\mathbb{N}^*}|x < 5} \right\}\). Chọn cách viết đúng của tập hợp \(M\) trong các cách sau:

A. \(M = \left\{ {0;1;2;3;4} \right\}\).

B. \(M = \left\{ {0;1;2;3;4;5} \right\}\).

C. \(M = \left\{ {1;2;3;4} \right\}\).

D. \(M = \left[ {1;2;3;4} \right]\).

Bài 5: Ta biết N là tập hợp các số tự nhiên. Gọi P là tập hợp các phân số. Khi đó:

A. \(5 \in N\) và \(5 \in P\).

B. \(5 \in N\) và \(5 \notin P\).

C. \(5 \notin N\) và \(5 \in P\).

D. \(5 \notin N\) và \(5 \notin P\).

Bài 6: Hệ Mặt Trời gồm có Mặt Trời ở trung tâm và 8 thiên thể quay quanh Mặt Trời gọi là các hành tinh. Đó là sao Thủy, Sao Kim, Trái Đất, Sao Hỏa, Sao Mộc, Sao Thổ, Sao Thiên Vương, Sao Hải Vương.

Cho S là tập hợp các hành tinh của Hệ Mặt Trời.

Xét tính đúng sai của các khẳng định sau:

a) S là tập hợp có 9 phần tử.

b) S = {Sao Thủy; Sao Kim; Trái Đất; Sao Hỏa; Sao Mộc; Sao Thổ; Sao Thiên Vương; Sao Hải Vương}.

c) Sao Thủy không thuộc S.

d) Mặt Trời là một phần tử của S.

Bài 7: Cho tập hợp P là tập hợp các chữ cái có trong từ NGÂN HÀNG

a) Điền kí hiệu \( \in ; \notin \) thích hợp vào ô trống

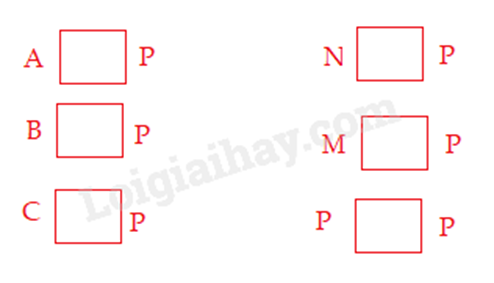
b) Viết tập hợp P.

Bài 8: Cho B là tập hợp các số tự nhiên chẵn, nhỏ hơn 8. Viết tập hợp B theo 2 cách.

Bài 9:

a) Viết tập hợp P gồm các số tự nhiên lớn hơn 50 và không lớn hơn 57.

b) Viết tập hợp \(A = \left\{ {x|33 < x \le 38} \right\}\) dưới dạng liệt kê các phần tử.

c) Viết tập hợp \(N = \left\{ {0;2;4;6;8} \right\}\) bằng cách chỉ ra tính chất đặc trưng.

d) Viết tập hợp E trong hình vẽ sau:

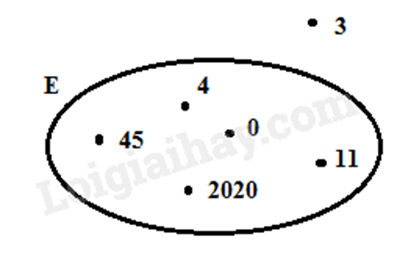
Bài 10: Cho tập hợp M = {1;2;3;4;5;6}; N = {8;7;6;5;4}.

a) Viết tập hợp A gồm các phần tử thuộc cả M và N.

b) Viết tập hợp B gồm các phần tử thuộc M nhưng không thuộc N.

c) Viết tập hợp C gồm các phần tử thuộc N nhưng không thuộc M.

----HẾT----

Lời giải chi tiết:

Bài 1: Theo Âm Lịch, năm 2024 là năm Giáp Thìn, tức năm con Rồng – xếp thứ năm trong 12 con giáp. Năm Giáp Thìn sẽ bắt đầu từ ngày 10/02/2024 và kết thúc năm vào ngày 28/01/2025 theo lịch dương. Gọi A là tập hợp các chữ số xuất hiện ở hình bên. Khi đó

A. \(A = \left\{ {4;2;0;2} \right\}\).

B. \(A = \left\{ {2;0;2;4} \right\}\).

C. \(A = \left\{ {0;2;4} \right\}\).

D. \(A = \left\{ {0;2} \right\}\).

Phương pháp

Dựa vào kiến thức về tập hợp.

Lời giải

Trong hình có các số 2; 0; 4 xuất hiện nên tập A là: \(A = \left\{ {0;2;4} \right\}\).

Đáp án: C

Bài 2: Viết tập hợp sau bằng cách liệt kê các phần tử \(A = \left\{ {\left. {x \in {\mathbb{N}^*}} \right|2021 < x \le 2023} \right\}\)

A. \(A = \left\{ {2022,{\mkern 1mu} 2023} \right\}\).

B. \(A = \left\{ {2022} \right\}\).

C. \(A = \left\{ {2022;{\mkern 1mu} 2023} \right\}\).

D. \(A = \left\{ {2023} \right\}\).

Phương pháp

- Tập hợp gồm các số lớn hơn 2021 và nhỏ hơn hoặc bằng 2023.

- Các phần tử trong tập hợp được ngăn cách bởi dấu ";" để không bị nhầm lẫn với số thập phân.

Lời giải

Tập hợp \(A = \left\{ {x \in \mathbb{N}*|2021 < x \le 2023} \right\}\) được viết bằng cách liệt kê là: \(A = \left\{ {2022;{\mkern 1mu} 2023} \right\}\)

Đáp án: C

Bài 3: Cho tập hợp E gồm các chữ cái trong từ “TOÁN HỌC”. Cách viết nào đúng?

A. E = {T; A; N; H; O; C}.

B. E = [T; O; A; N; H; C].

C. E = (T; O; A; N; H; C).

D. E = {T; O; A; N; H; O; C}.

Phương pháp

Ta liệt kê các chữ cái xuất hiện trong từ "TOÁN HỌC", với những chữ cái xuất hiện 2 lần ta chỉ viết 1 lần vào tập hợp.

Lời giải

Các chữ trong từ “TOÁN HỌC” gồm T; O; A; N; H; O; C.

Tập hợp E = {T; A; N; H; O; C}

Đáp án: A

Bài 4: Cho tập hợp \(\left\{ {x \in {\mathbb{N}^*}|x < 5} \right\}\). Chọn cách viết đúng của tập hợp \(M\) trong các cách sau:

A. \(M = \left\{ {0;1;2;3;4} \right\}\).

B. \(M = \left\{ {0;1;2;3;4;5} \right\}\).

C. \(M = \left\{ {1;2;3;4} \right\}\).

D. \(M = \left[ {1;2;3;4} \right]\).

Phương pháp

- \({\mathbb{N}^*}\) là tập hợp các số tự nhiên lớn hơn \(0\).

- Cách viết tập hợp ta sử dụng dấu ngoặc nhọn.

Lời giải

\({\mathbb{N}^*}\) là tập hợp các số tự nhiên lớn hơn \(0\). Do đó các phần tử thuộc tập hợp \(M\) là các số tự nhiên lớn hơn \(0\) và nhỏ hơn \(5\) đó là 1; 2; 3; 4.

Vậy cách viết khác của tập hợp M là \(M = \left\{ {1;2;3;4} \right\}\).

Đáp án: C

Bài 5: Ta biết N là tập hợp các số tự nhiên. Gọi P là tập hợp các phân số. Khi đó:

A. \(5 \in N\) và \(5 \in P\).

B. \(5 \in N\) và \(5 \notin P\).

C. \(5 \notin N\) và \(5 \in P\).

D. \(5 \notin N\) và \(5 \notin P\).

Phương pháp

Mô tả tập hợp N và P.

Lời giải

Vì \(5 = \frac{5}{1}\) nên 5 là số tự nhiên và 5 là phân số.

Do đó \(5 \in N\) và \(5 \in P\).

Đáp án: A

Bài 6: Hệ Mặt Trời gồm có Mặt Trời ở trung tâm và 8 thiên thể quay quanh Mặt Trời gọi là các hành tinh. Đó là sao Thủy, Sao Kim, Trái Đất, Sao Hỏa, Sao Mộc, Sao Thổ, Sao Thiên Vương, Sao Hải Vương.

Cho S là tập hợp các hành tinh của Hệ Mặt Trời.

Xét tính đúng sai của các khẳng định sau:

a) S là tập hợp có 9 phần tử.

b) S = {Sao Thủy; Sao Kim; Trái Đất; Sao Hỏa; Sao Mộc; Sao Thổ; Sao Thiên Vương; Sao Hải Vương}.

c) Sao Thủy không thuộc S.

d) Mặt Trời là một phần tử của S.

Phương pháp

+) Số hành tinh là số phần tử của S.

+) Các hành tinh của Hệ Mặt Trời là sao Thủy, Sao Kim, Trái Đất, Sao Hỏa, Sao Mộc, Sao Thổ, Sao Thiên Vương, Sao Hải Vương.

+) Các phần tử của một tập hợp được viết trong hai dấu ngoặc nhọn { }, ngăn cách nhau bởi dấu  “ ; ”.

+) Mỗi một hành tinh là một phần tử của tập hợp.

+) Mặt Trời là một ngôi sao trung tâm của Hệ Mặt Trời nên ta không tính là một hành tinh.

Lời giải

a) Sai

Hệ Mặt Trời có 8 hành tinh nên S có 8 phần tử.

b) Đúng

Có 8 hành tinh: Sao Thủy; Sao Kim; Trái Đất; Sao Hỏa; Sao Mộc; Sao Thổ; Sao Thiên Vương; Sao Hải Vương nên S = {Sao Thủy; Sao Kim; Trái Đất; Sao Hỏa; Sao Mộc; Sao Thổ; Sao Thiên Vương; Sao Hải Vương}.

c) Sai

Sao Thủy là một hành tinh của Hệ Mặt Trời.

d) Sai

Mặt Trời không là hành tinh nên Mặt Trời không là một phần tử của S

Đáp án: SĐSS

Bài 7: Cho tập hợp P là tập hợp các chữ cái có trong từ NGÂN HÀNG

a) Điền kí hiệu \( \in ; \notin \) thích hợp vào ô trống

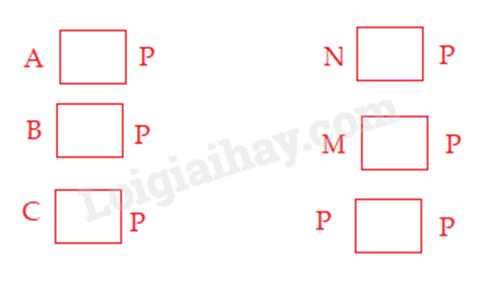
b) Viết tập hợp P.

Phương pháp

Phần tử x thuộc tập hợp A được kí hiệu là \(x \in A\), y không thuộc tập hợp A được kí hiệu là \(y \notin A\)

Viết tập hợp bằng cách liệt kê các phần tử của tập hợp

+ Các phần tử của một tập hợp được viết trong hai dấu ngoặc nhọn { }, ngăn cách nhau bởi dấu  “ ; ”

+ Mỗi phần tử được liệt kê một lần , thứ tự liệt kê tùy ý.

Lời giải

a)

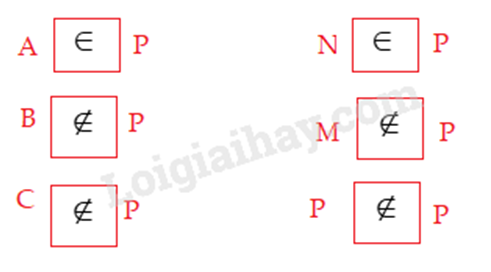
b) P = {N;G;Â;H;A}

Bài 8: Cho B là tập hợp các số tự nhiên chẵn, nhỏ hơn 8. Viết tập hợp B theo 2 cách.

Phương pháp

Cách 1: Liệt kê các phần tử của tập hợp

+ Các phần tử của một tập hợp được viết trong hai dấu ngoặc nhọn { }, ngăn cách nhau bởi dấu  “ ; ”

+ Mỗi phần tử được liệt kê một lần , thứ tự liệt kê tùy ý.

Cách 2: Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp đó

Lời giải

Cách 1: B = {0;2;4;6}

Cách 2: B = {x \( \in \)N| x là số chẵn nhỏ hơn 8}

Bài 9:

a) Viết tập hợp P gồm các số tự nhiên lớn hơn 50 và không lớn hơn 57.

b) Viết tập hợp \(A = \left\{ {x|33 < x \le 38} \right\}\) dưới dạng liệt kê các phần tử.

c) Viết tập hợp \(N = \left\{ {0;2;4;6;8} \right\}\) bằng cách chỉ ra tính chất đặc trưng.

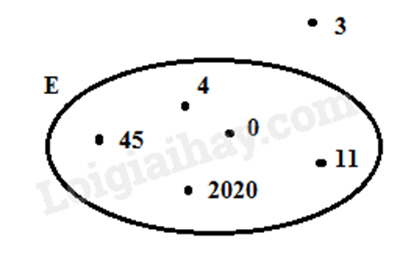
d) Viết tập hợp E trong hình vẽ sau:

Phương pháp

a) Viết tập hợp P dưới dạng liệt kê.

b) + Chỉ ra các số lớn hơn 33 và nhỏ hơn hoặc bằng 38

+ Từ đó viết tập hợp A dưới dạng liệt kê.

c) Tìm tính chất của các số 0; 2; 4; 6; 8.

Cách viết tập hợp chỉ ra tính chất đặc trưng:

\(N = \){\(x\)| tính chất của \(x\)}

d) Các phần tử nằm trong vòng tròn là các phần tử thuộc tập hợp E.

Lời giải

a) Các số tự nhiên lớn hơn 50 và không lớn hơn 57 là 51; 52; 53; 54; 55; 56; 57

Nên \(P = \left\{ {51;52;53;54;55;56;57} \right\}\)

b) Các số lớn hơn 33 và nhỏ hơn hoặc bằng 38 là 34; 35; 36; 37; 38.

Nên \(A = \left\{ {34;35;36;37;38} \right\}\)

c) Cách 1.

Các số 0; 2; 4; 6; 8 là các số tự nhiên chẵn và nhỏ hơn 9

Ta có tập hợp \(N = \) {\(x\)| \(x\) là số tự nhiên chẵn, \(x < 9\)}

Cách 2.

Các số 0;2;4;6;8 là các số tự nhiên chẵn nhỏ hơn 10

Ta có tập hợp \(N = \) {\(x\)| \(x\) là số tự nhiên chẵn, \(x < 10\)}

d) Ta có các số trong vòng tròn là 0; 4; 11; 45; 2020 nên tập hợp \(E = \left\{ {0;4;11;45;2020} \right\}\).

Bài 10: Cho tập hợp M = {1;2;3;4;5;6}; N = {8;7;6;5;4}.

a) Viết tập hợp A gồm các phần tử thuộc cả M và N.

b) Viết tập hợp B gồm các phần tử thuộc M nhưng không thuộc N.

c) Viết tập hợp C gồm các phần tử thuộc N nhưng không thuộc M.

Phương pháp

Bước 1: Tìm các phần tử của mỗi tập hợp

Bước 2: Viết tập hợp bằng cách liệt kê các phần tử của tập hợp:

+ Các phần tử của một tập hợp được viết trong hai dấu ngoặc nhọn { }, ngăn cách nhau bởi dấu  “ ; ”

+ Mỗi phần tử được liệt kê một lần , thứ tự liệt kê tùy ý.

Lời giải

a) Các phần tử thuộc cả M và N là: 4;5;6.

Vậy A = {4;5;6}.

b) Các phần tử thuộc M nhưng không thuộc N là: 1;2;3

Vậy B = {1;2;3}.

c) Các phần tử thuộc N nhưng không thuộc M là: 8;7.

Vậy C = {8;7}.