Đề ôn hè Toán 6 lên 7 - Đề 10

Đề bài

Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:

Câu 1: Số đối của \(2025\) là

A. \(2025\).

B. \( - 2025\).

C. \(0\).

D. \(\frac{1}{{2025}}\).

Câu 2: Giá trị của biểu thức \( - 156 + x\) tại \(x =  - 26\) bằng

A. \( - 130\).

B. \(130\).

C. \( - 182\).

D. \(182\).

Câu 3: Số ước nguyên của số 6 là

A. \(8\).

B. \(4\).

C. \(3\).

D. \(6\).

Câu 4: Hình vuông có bao nhiêu trục đối xứng?

A. \(2\).

B. \(3\).

C. \(4\).

D. \(6\).

Câu 5: Mảnh đất hình thoi có độ dài hai đường chéo là \(12\,{\rm{m}}\) và \(11\,{\rm{m}}\). Diện tích mảnh đất là

A. \(131\,{{\rm{m}}^2}\).

B. \(132\,{{\rm{m}}^2}\).

C. \(65\,{{\rm{m}}^2}\).

D. \(66\,{{\rm{m}}^2}\).

Câu 6: Số nghịch đảo của \(75\% \) là

A. \( - \frac{3}{4}\).

B. \(\frac{4}{3}\).

C. \( - \frac{4}{3}\).

D. \(\frac{3}{4}\).

Câu 7: Biểu đồ tranh dưới đây cho biết số lượt ô tô gửi tại một bãi đỗ xe vào các ngày trong một tuần.

Số lượt ô tô đã gửi xe vào ngày thứ hai và thứ ba là bao nhiêu?

A. \(300\).

B. \(630\).

C. \(11\).

D. \(330\).

Câu 8: Biểu đồ cho biết số lượng các bạn nam, nữ trong lớp \(6A\) yêu thích ba môn học (mỗi bạn chỉ được chọn một môn).

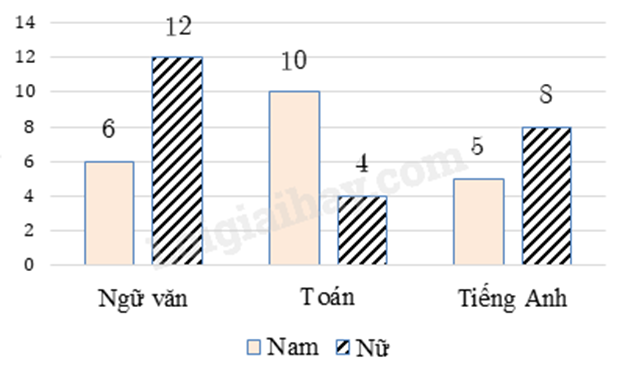
Tỉ lệ học sinh nữ yêu thích môn Ngữ văn so với cả lớp là

A. \(\frac{4}{{15}}\).

B. \(\frac{5}{{12}}\)

C. \(\frac{{15}}{4}\).

D. \(\frac{{12}}{5}\).

Câu 9: Trong hộp có 1 viên bi vàng, 1 viên bi xanh lá, 1 viên bi đỏ và 1 viên bi màu xanh da trời. Dũng thực hiện lấy 1 viên bi trong hộp, ghi lại màu sắc rồi lại bỏ vào hộp. Sau khi thực hiện việc đó 12 lần, Dũng thu được kết quả như sau:

V: bi màu vàng; Đ: bi màu đỏ; XL: bi màu xanh lá; XT: bi màu xanh da trời.

Xác suất của sự kiện Dũng lấy được bi màu vàng là

A. \(\frac{1}{3}\).

B. \(\frac{5}{{12}}\).

C. \(\frac{1}{2}\).

D. \(\frac{1}{4}\).

Câu 10: An thấy rằng \(40\% \) số học sinh của lớp 6A là \(20\) học sinh. Vậy lớp 6A có số học sinh là

A. \(45\)học sinh.

B. \(40\)học sinh.

C. \(50\)học sinh.

D. \(8\)học sinh.

Câu 11: Trong hình vẽ dưới đây, số đo \(\widehat {mOn}\) bằng bao nhiêu độ?

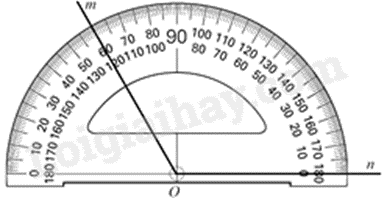
A. \(180^\circ \).

B. \(60^\circ \).

C. \(120^\circ \).

D. \(125^\circ \).

Câu 12: Cho điểm \(M\) là trung điểm của đoạn \(AB\), biết \(AB = 6\)\(cm\). Khi đó độ dài của đoạn \(MA\) bằng

A. \(2\)\(cm\).

B. \(4\)\(cm\).

C. \(3\)\(cm\).

D. \(6\)\(cm\).

Phần tự luận (7 điểm)

Bài 1. (1,5 điểm)

1) Thực hiện phép tính

a) \(\left( { - 4,2} \right).5,6 + 5,6.\left( { - 5,8} \right) + 2,8\);

b) \(75\%  - 1\frac{1}{2} + 0,5:\frac{5}{{12}}\).

2) Tìm \(x\) biết  \(\frac{1}{4} + \frac{3}{4}:x = \frac{1}{6}\).

Bài 2. (1 điểm) Hưởng ứng phong trào ngày chủ nhật xanh nhà trường muốn chia 156 em học sinh nam và 132 em học sinh nữ của khối 8 và 9 thành một số nhóm như nhau gồm cả nam và nữ để tham gia lao động, vệ sinh. Hỏi có thể chia được nhiều nhất là bao nhiêu nhóm, khi đó mỗi nhóm có bao nhiêu bạn nam, bao nhiêu bạn nữ?

Bài 3. (1 điểm) Cho biểu đồ tranh biểu diễn số gạo xuất khẩu của Việt Nam qua các năm:

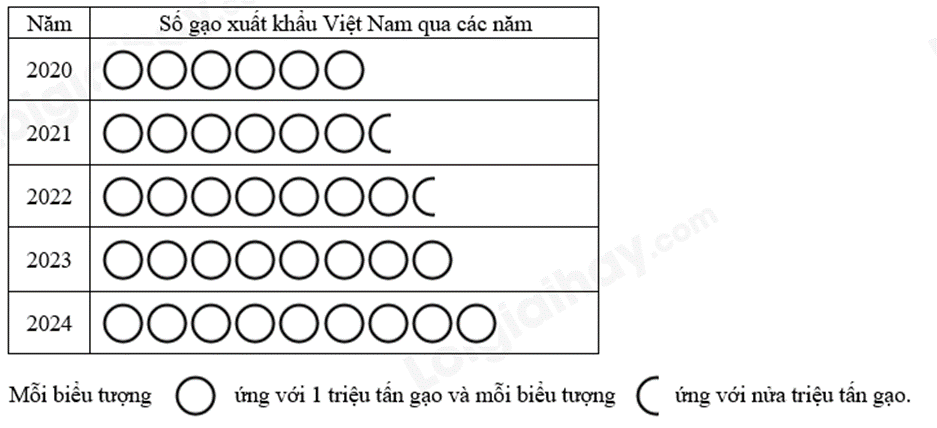
a) Năm nào Việt Nam có số lượng gạo xuất khẩu đạt nhiều nhất? Và năm đó, Việt Nam xuất khẩu gạo nhiều hơn năm 2021 là bao nhiêu?

b) Tính tỉ số của số lượng gạo xuất khẩu năm 2024 và tổng số lượng gạo xuất khẩu của cả 5 năm.

Bài 4. (1 điểm) Sân nhà bà Hà có dạng hình chữ nhật với chiều dài \(9\,m\), chiều rộng ngắn hơn chiều dài \(5m\).

a) Tính diện tích sân nhà bà Hà.

b) Bà Hà để lại \(8\) ô đất hình vuông cạnh \(1\,m\) để trồng cây, phần đất còn lại được lát bằng loại gạch hình vuông cạnh \(40cm\). Hỏi cần dùng bao nhiêu viên gạch? (Diện tích phần mạch lát không đáng kể).

Bài 5. (1,5 điểm) Cho hai tia \(Ox\) và \(Oy\) đối nhau. Lấy điểm \(M\) thuộc tia \(Ox\), điểm \(N\) thuộc tia \(Oy\) sao cho \(OM = 6\)\(cm\),\(ON = 3\)\(cm\).

a) Tính độ dài đoạn \(MN\).

b) Gọi  \(E\) là trung điểm của \(OM\). Hỏi \(O\) có là trung điểm của đoạn \(EN\) không? Vì sao?

c) Lấy điểm \(C\) nằm ngoài đường thẳng \(xy\). Kẻ tia \(OC\), kể tên các góc đỉnh \(O\) và chỉ ra góc tù (nếu có) trong hình vẽ.

-------- Hết --------

Lời giải

Phần trắc nghiệm

Câu 1: Số đối của \(2025\) là

A. \(2025\).

B. \( - 2025\).

C. \(0\).

D. \(\frac{1}{{2025}}\).

Phương pháp

Số đối của số a là –a.

Lời giải

Số đối của 2025 là -2025.

Đáp án: B

Câu 2: Giá trị của biểu thức \( - 156 + x\) tại \(x =  - 26\) bằng

A. \( - 130\).

B. \(130\).

C. \( - 182\).

D. \(182\).

Phương pháp

Thay \(x =  - 26\) vào biểu thức và thực hiện cộng hai số nguyên cùng dấu:

\(\left( { - a} \right) + \left( { - b} \right) =  - \left( {a + b} \right)\).

Lời giải

Thay \(x =  - 26\) vào biểu thức, ta được:

\( - 156 + \left( { - 26} \right) =  - \left( {156 + 26} \right) =  - 182\).

Đáp án: C

Câu 3: Số ước nguyên của số 6 là

A. \(8\).

B. \(4\).

C. \(3\).

D. \(6\).

Phương pháp

Liệt kê các ước nguyên dương.

Ước nguyên bao gồm ước nguyên dương và các số đối của chúng.

Lời giải

Ta có: 6 = 2.3 nên các ước nguyên dương của 6 là: 1; 2; 3; 6.

Suy ra các ước nguyên của số 6 là: 1; 2; 3; 6; -1; -2; -3; -6.

Vậy có 8 ước nguyên của số 6.

Đáp án: A

Câu 4: Hình vuông có bao nhiêu trục đối xứng?

A. \(2\).

B. \(3\).

C. \(4\).

D. \(6\).

Phương pháp

Trục đối xứng là đường thẳng chia hình thành hai phần mà khi ta “gấp” hình theo đường thẳng đó thì hai phần “chồng khít” lên nhau.

Lời giải

Hình vuông có 4 trục đối xứng.

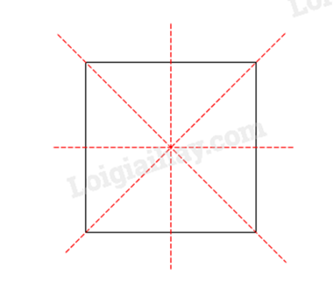
Đáp án: C

Câu 5: Mảnh đất hình thoi có độ dài hai đường chéo là \(12\,{\rm{m}}\) và \(11\,{\rm{m}}\). Diện tích mảnh đất là

A. \(131\,{{\rm{m}}^2}\).

B. \(132\,{{\rm{m}}^2}\).

C. \(65\,{{\rm{m}}^2}\).

D. \(66\,{{\rm{m}}^2}\).

Phương pháp

Diện tích hình thoi tính theo công thức: \(S = \frac{1}{2}mn\) với m, n lần lượt là độ dài hai đường chéo.

Lời giải

Diện tích mảnh đất là: \(\frac{1}{2}.12.11 = 66\left( {{m^2}} \right)\).

Đáp án: D

Câu 6: Số nghịch đảo của \(75\% \) là

A. \( - \frac{3}{4}\).

B. \(\frac{4}{3}\).

C. \( - \frac{4}{3}\).

D. \(\frac{3}{4}\).

Phương pháp

Số nghịch đảo của một số a là \(\frac{1}{a}\).

Lời giải

Ta có: \(75\%  = \frac{{75}}{{100}} = \frac{3}{4}\).

Số nghịch đảo của \(\frac{3}{4}\) là \(1:\frac{3}{4} = \frac{4}{3}\).

Vậy số nghịch đảo của 75% là \(\frac{4}{3}\).

Đáp án: B

Câu 7: Biểu đồ tranh dưới đây cho biết số lượt ô tô gửi tại một bãi đỗ xe vào các ngày trong một tuần.

Số lượt ô tô đã gửi xe vào ngày thứ hai và thứ ba là bao nhiêu?

A. \(300\).

B. \(630\).

C. \(11\).

D. \(330\).

Phương pháp

Xác định tổng số biểu tượng của ngày thứ hai và thứ ba.

Số lượt ô tô = số ô tô ứng với mỗi biểu tượng . số biểu tượng.

Lời giải

Số biểu tượng của ngày thứ hai và thứ ba là:

5 + 6 = 11 (biểu tượng)

Vì mỗi biểu tượng ứng với 30 ô tô nên số lượt ô tô đã gửi xe vào ngày thứ hai và thứ ba là:

30 . 11 = 330 (lượt ô tô).

Đáp án: D

Câu 8: Biểu đồ cho biết số lượng các bạn nam, nữ trong lớp \(6A\) yêu thích ba môn học (mỗi bạn chỉ được chọn một môn).

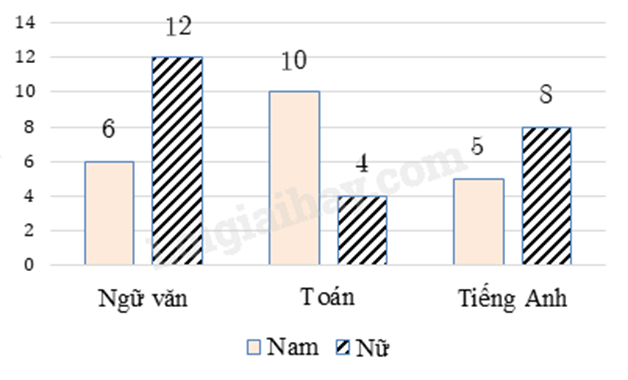
Tỉ lệ học sinh nữ yêu thích môn Ngữ văn so với cả lớp là

A. \(\frac{4}{{15}}\).

B. \(\frac{5}{{12}}\)

C. \(\frac{{15}}{4}\).

D. \(\frac{{12}}{5}\).

Phương pháp

Tính tổng số học sinh cả lớp.

Tính tỉ số học sinh nữ = số học sinh nữ : tổng số học sinh cả lớp.

Lời giải

Tổng số học sinh cả lớp là:

6 + 12 + 10 + 4 + 5 + 8 = 45 (học sinh)

Tỉ lệ học sinh nữ yêu thích môn Ngữ văn so với cả lớp là: \(\frac{{12}}{{45}} = \frac{4}{{15}}\).

Đáp án: A

Câu 9: Trong hộp có 1 viên bi vàng, 1 viên bi xanh lá, 1 viên bi đỏ và 1 viên bi màu xanh da trời. Dũng thực hiện lấy 1 viên bi trong hộp, ghi lại màu sắc rồi lại bỏ vào hộp. Sau khi thực hiện việc đó 12 lần, Dũng thu được kết quả như sau:

V: bi màu vàng; Đ: bi màu đỏ; XL: bi màu xanh lá; XT: bi màu xanh da trời.

Xác suất của sự kiện Dũng lấy được bi màu vàng là

A. \(\frac{1}{3}\).

B. \(\frac{5}{{12}}\).

C. \(\frac{1}{2}\).

D. \(\frac{1}{4}\).

Phương pháp

Xác định số lần lấy được bi màu vàng.

Xác suất của sự kiện lấy được bi màu vàng = số lần lấy được bi màu vàng : tổng số lần thực hiện.

Lời giải

Từ dãy dữ liệu trên, ta thấy số lần lấy được bi màu vàng là 3 lần.

Xác suất của sự kiện Dũng lấy được bi màu vàng là: \(\frac{3}{{12}} = \frac{1}{4}\).

Đáp án: D

Câu 10: An thấy rằng \(40\% \) số học sinh của lớp 6A là \(20\) học sinh. Vậy lớp 6A có số học sinh là

A. \(45\)học sinh.

B. \(40\)học sinh.

C. \(50\)học sinh.

D. \(8\)học sinh.

Phương pháp

Tìm số a khi biết m% của a là b, ta lấy: a = b : m%.

Lời giải

Lớp 6A có số học sinh là: 20 : 40% = 50 (học sinh).

Đáp án: C

Câu 11: Trong hình vẽ dưới đây, số đo \(\widehat {mOn}\) bằng bao nhiêu độ?

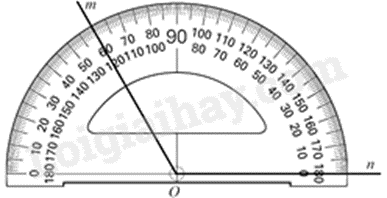
A. \(180^\circ \).

B. \(60^\circ \).

C. \(120^\circ \).

D. \(125^\circ \).

Phương pháp

Quan sát hình vẽ để xác định góc.

Lời giải

Số đo \(\widehat {mOn} = 120^\circ \).

Đáp án: C

Câu 12: Cho điểm \(M\) là trung điểm của đoạn \(AB\), biết \(AB = 6\)\(cm\). Khi đó độ dài của đoạn \(MA\) bằng

A. \(2\)\(cm\).

B. \(4\)\(cm\).

C. \(3\)\(cm\).

D. \(6\)\(cm\).

Phương pháp

Nếu M là trung điểm của AB thì MA = MB = \(\frac{{AB}}{2}\).

Lời giải

Vì M là trung điểm của AB nên MA = \(\frac{{AB}}{2} = \frac{6}{2} = 3\left( {cm} \right)\).

Đáp án: C

Phần tự luận.

Bài 1. (1,5 điểm)

1) Thực hiện phép tính

a) \(\left( { - 4,2} \right).5,6 + 5,6.\left( { - 5,8} \right) + 2,8\);

b) \(75\%  - 1\frac{1}{2} + 0,5:\frac{5}{{12}}\).

2) Tìm \(x\) biết  \(\frac{1}{4} + \frac{3}{4}:x = \frac{1}{6}\).

Phương pháp

1) Kết hợp phép tính với số thập phân và phân số, hỗn số, tỉ số phần trăm.

2) Chuyển vế để tìm \(x\).

Lời giải

1)

a) \(\left( { - 4,2} \right).5,6 + 5,6.\left( { - 5,8} \right) + 2,8\)

\( = 5,6.\left[ {\left( { - 4,2} \right) + \left( { - 5,8} \right)} \right] + 2,8\)

\(\begin{array}{l} = 5,6.\left( { - 10} \right) + 2,8\\ =  - 56 + 2,8\\ =  - 53,2\end{array}\)

b) \(75\%  - 1\frac{1}{2} + 0,5:\frac{5}{{12}}\)

\(\begin{array}{l} = \frac{3}{4} - \frac{3}{2} + \frac{1}{2}.\frac{{12}}{5}\\ =  - \frac{3}{4} + \frac{6}{5}\\ = \frac{9}{{20}}\end{array}\)

2)

\(\begin{array}{l}\frac{1}{4} + \frac{3}{4}:x = \frac{1}{6}\\\frac{3}{4}:x = \frac{{ - 1}}{{12}}\\x = \frac{3}{4}:\frac{{ - 1}}{{12}}\\x =  - 9\end{array}\)

Vậy \(x =  - 9\).

Bài 2. (1 điểm) Hưởng ứng phong trào ngày chủ nhật xanh nhà trường muốn chia 156 em học sinh nam và 132 em học sinh nữ của khối 8 và 9 thành một số nhóm như nhau gồm cả nam và nữ để tham gia lao động, vệ sinh. Hỏi có thể chia được nhiều nhất là bao nhiêu nhóm, khi đó mỗi nhóm có bao nhiêu bạn nam, bao nhiêu bạn nữ?

Phương pháp

Gọi số nhóm được chia là a, \(\left( {a \in {\mathbb{N}^*}} \right)\)

Vì số nhóm chia được là nhiều nhất nên a = ƯCLN(156;132).

Phân tích số 156 và số 132 để tìm ƯCLN.

Suy ra giá trị của a.

Tính số học sinh trong mỗi nhóm = tổng số học sinh : số nhóm.

Lời giải

Gọi số nhóm được chia là a, \(\left( {a \in {\mathbb{N}^*}} \right)\)

Vì số nhóm chia được là nhiều nhất nên a = ƯCLN(156;132).

Ta có:

\(156 = {2^2}.3.13\)

\(132 = {2^2}.3.11\)

suy ra ƯCLN(156;132) = \({2^3}.3 = 12\)

Do đó a = 12

Vậy có thể chia được nhiều nhất 12 nhóm.

Khi đó:

+ số bạn nam trong một nhóm là: 156 : 12 = 13 (bạn)

+ số bạn nữ trong một nhóm là: 132 : 12 = 11 (bạn)

Bài 3. (1 điểm) Cho biểu đồ tranh biểu diễn số gạo xuất khẩu của Việt Nam qua các năm:

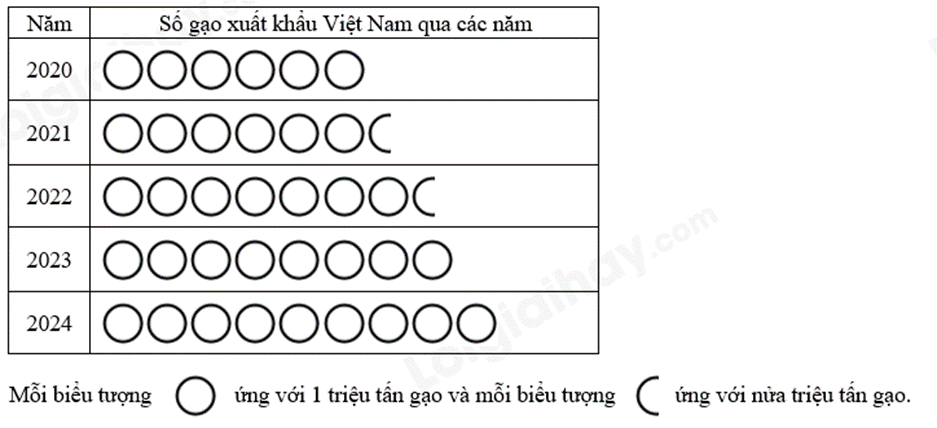
a) Năm nào Việt Nam có số lượng gạo xuất khẩu đạt nhiều nhất? Và năm đó, Việt Nam xuất khẩu gạo nhiều hơn năm 2021 là bao nhiêu?

b) Tính tỉ số của số lượng gạo xuất khẩu năm 2024 và tổng số lượng gạo xuất khẩu của cả 5 năm.

Phương pháp

a) So sánh số lượng biểu tượng các năm để xác định năm có số lượng gạo xuất khẩu đạt nhiều nhất.

Tính số lượng gạo xuất khẩu năm đó và số lượng gạo năm 2021 rồi thực hiện trừ để tìm số gạo nhiều hơn.

b) Tính tổng số lượng gạo xuất khẩu của cả 5 năm.

Tỉ số của số lượng gạo năm 2024 = số lượng gạo năm 2024 : tổng số lượng gạo.

Lời giải

a) Nửa triệu = 0,5 triệu.

Năm 2024 Việt Nam có số lượng gạo xuất khẩu đạt nhiều nhất vì số biểu tượng nhiều nhất.

Năm 2024, số lượng gạo xuất khẩu được ứng với 9 biểu tượng  nên số lượng gạo là: 9.1 = 9 (triệu tấn gạo)

Năm 2021, số lượng gạo xuất khẩu được ứng với 6 biểu tượng  và 1 biểu tượng  nên số lượng gạo là: 6.1 + 1.0,5 = 6,5 (triệu tấn gạo).

Do đó năm 2024 Việt Nam xuất khẩu gạo nhiều hơn năm 2021 là: 9 – 6,5 = 2,5 (triệu tấn gạo)

b) Tổng số biểu tượng của cả 5 năm là 36 biểu tượng  và 2 biểu tượng  nên tổng số lượng gạo xuất khẩu của cả 5 năm là: 36.1 + 2.0,5 = 37 (triệu tấn gạo)

Tỉ số của số lượng gạo xuất khẩu năm 2024 và tổng số lượng gạo xuất khẩu của cả 5 năm là: \(\frac{9}{{37}}\).

Bài 4. (1 điểm) Sân nhà bà Hà có dạng hình chữ nhật với chiều dài \(9\,m\), chiều rộng ngắn hơn chiều dài \(5m\).

a) Tính diện tích sân nhà bà Hà.

b) Bà Hà để lại \(8\) ô đất hình vuông cạnh \(1\,m\) để trồng cây, phần đất còn lại được lát bằng loại gạch hình vuông cạnh \(40cm\). Hỏi cần dùng bao nhiêu viên gạch? (Diện tích phần mạch lát không đáng kể).

Phương pháp

a) Tính chiều rộng sân theo chiều dài.

Tính diện tích sân bằng công thức tính diện tích hình chữ nhật: S = chiều dài . chiều rộng.

b) Tính diện tích mỗi viên gạch bằng công thức tính diện tích hình vuông: S = cạnh . cạnh.

Đổi về cùng đơn vị.

Tính diện tích phần đất còn lại được lát gạch.

Tính số viên gạch = diện tích phần đất : diện tích một viên gạch.

Lời giải

a) Chiều rộng sân nhà bà Hà là:

\(9 - 5 = 4(m)\)

Diện tích sân nhà bà Hà là:

\(9.4 = 36{\mkern 1mu} ({m^2})\)

b) Một viên gạch có diện tích là \(40.40 = 1600\left( {c{m^2}} \right) = 0,16\left( {{m^2}} \right)\).

Diện tích đất còn lại sau khi để lại 8 ô trồng cây là:

\(36 - 8.1.1 = 28\left( {{m^2}} \right)\)

Số viên gạch cần dùng là:

\(28:0,16 = 175\) (viên).

Vậy cần dùng 175 viên gạch.

Bài 5. (1,5 điểm) Cho hai tia \(Ox\) và \(Oy\) đối nhau. Lấy điểm \(M\) thuộc tia \(Ox\), điểm \(N\) thuộc tia \(Oy\) sao cho \(OM = 6\)\(cm\),\(ON = 3\)\(cm\).

a) Tính độ dài đoạn \(MN\).

b) Gọi  \(E\) là trung điểm của \(OM\). Hỏi \(O\) có là trung điểm của đoạn \(EN\) không? Vì sao?

c) Lấy điểm \(C\) nằm ngoài đường thẳng \(xy\). Kẻ tia \(OC\), kể tên các góc đỉnh \(O\) và chỉ ra góc tù (nếu có) trong hình vẽ.

Phương pháp

a) Sử dụng kiến thức điểm nằm giữa hai điểm để tính độ dài MN.

b) Sử dụng kiến thức về trung điểm: Trung điểm của đoạn thẳng chia đoạn thẳng đó thành hai phần bằng nhau.

c) Quan sát hình vẽ để xác định các góc.

Góc tù là góc lớn \(90^\circ \) và nhỏ hơn \(180^\circ \).

Lời giải

a) Ta có điểm \(O\) nằm giữa \(M\) và \(N\) nên

\(\begin{array}{l}OM + ON = MM\\MN = 6 + 3 = 9\left( {{\rm{cm}}} \right)\end{array}\)

b) Điểm \(E\) là trung điểm của OM nên \(OE = EM = \frac{{OM}}{2} = \frac{6}{2} = 3{\mkern 1mu} cm\)

Mà \(ON = 3cm\)

Do đó \(ON = OE\)

Lại có \(O\) nằm giữa \(N\) và \(E\)

Nên \(O\) là trung điểm của NE.

c)

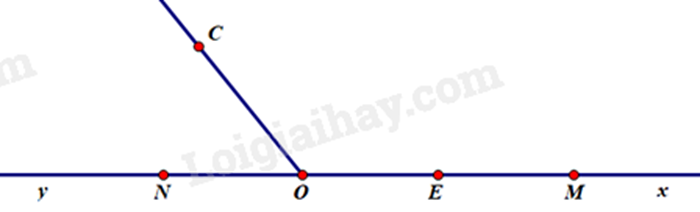
Các góc đỉnh A là   \(\widehat {xOy}\) , \(\widehat {xOC}\) và \(\widehat {yOC}\).

Trong trường hợp hình vẽ trên chỉ được góc tù là \(\widehat {xOC}\).