 Bài tập ôn hè môn Toán 6 lên 7, bộ đề ôn tập hè có lời giải chi tiết
Bài tập ôn hè môn Toán 6 lên 7, bộ đề ôn tập hè có lời giải chi tiết
 Ôn tập hè Chủ đề 10. Những hình hình học cơ bản
Ôn tập hè Chủ đề 10. Những hình hình học cơ bản Dạng 3. Góc, số đo góc Chủ đề 10 Ôn hè Toán 6
Tải về1. Góc * Góc là hình gồm hai tia chung gốc
Lý thuyết
1. Góc
* Góc là hình gồm hai tia chung gốc
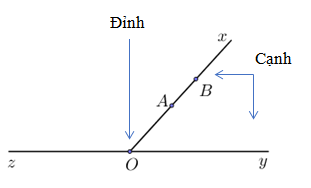
- Gốc chung là đỉnh của góc
- Hai tia là 2 cạnh của góc
- Điểm \(O\) là đỉnh của góc
- Hai tia \(Ox,Oy\) là hai cạnh của góc
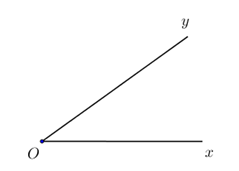
- Góc \(xOy\) (góc \(yOx\) hoặc góc \(O\) )
- Kí hiệu: \(\widehat {xOy},\,\widehat {yOx},\widehat O\)hoặc \(\angle xOy,\angle yOx,\angle O\)
- Góc \(xOy\) còn được gọi là góc \(AOB,\) góc \(BOA,\) góc \(yOx,\) góc \(O\)
- Chú ý: Khi viết kí hiệu góc, đỉnh góc viết ở giữa
- Khi \(Oy\) và \(Oz\) là hai tia đối nhau, ta có góc bẹt \(yOz\)
2. Đo góc
* Dụng cụ đo góc: Thước đo góc (thước đo độ)
* Cách đo góc \(xOy\)
- Đặt thước đo góc sao cho tâm của thước trùng với đỉnh \(O\) của góc
- Tia \(xOy\) đi qua vạch 0
\( \Rightarrow \) Khi đó: tia \(Oy\)đi qua vạch chỉ số đo của góc
Góc \(xOy\) có số đo là \({36^0}\)
- Mỗi góc có một số đo, số đo góc không vượt quá \({180^0}\)
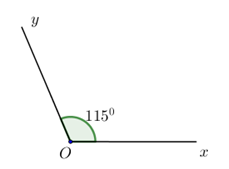
Góc \(mOn\) có số đo là \({130^0}\)
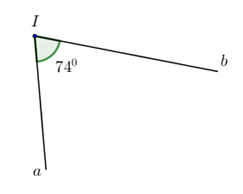
Góc \(aIb\) có số đo là \({74^0}\)
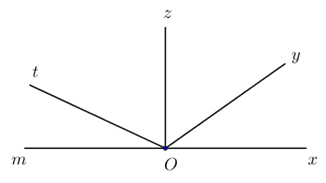
3. Các góc đặc biệt
Trên hình vẽ:
Góc \(xOy = {35^0}\) (góc nhọn)
Góc \(xOx = {90^0}\) (góc vuông)
Góc \(xOt = {155^0}\) (góc tù)
Góc \(xOm = {180^0}\) (góc bẹt)
Bài tập
Bài 1:
Điền vào chỗ chấm:
a) Góc \(yOz\) là hình gồm ……..
b) Góc bẹt là góc có …….
c) Khi hai tia \(Ox,Oy\) không đối nhau, \(M\) là điểm nằm trong góc \(xOy\) nếu…..
Bài 2:
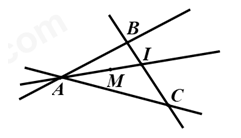
Cho ba điểm \(A,B,C\) không thẳng hàng. Kẻ các đường thẳng \(AB,AC,BC.\) Gọi \(M\) là điểm nằm trong góc \(ABC\) và góc \(ACB.\)
a) Chứng tỏ rằng \(M\) cũng nằm trong góc \(BAC.\)
b) Gọi \(I\) là giao điểm của hai đường thẳng \(AM\) và \(BC\). Hỏi điểm \(I\) nằm trong góc nào trong số các góc sau: \(\angle BAC,\angle BMC.\)
Bài 3:
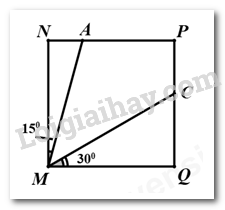
Cho hình vuông \(MNPQ\) và số đo các góc ghi tương ứng như hình sau:
a) Cho biết số đo của góc \(AMC\) bằng cách đo.
b) Sắp xếp góc góc \(NMA\), \(AMC\), \(CMQ\) theo thứ tự số đo tăng dần.
Trên tia \(Ox\) lấy hai điểm \(A\) và \(B\) sao cho \(OA = 3cm;\,\,OB = 6cm\).
Lời giải chi tiết:
Bài 1:
Điền vào chỗ chấm:
a) Góc \(yOz\) là hình gồm ……..
b) Góc bẹt là góc có …….
c) Khi hai tia \(Ox,Oy\) không đối nhau, \(M\) là điểm nằm trong góc \(xOy\) nếu…..
Phương pháp
Áp dụng định nghĩa góc, góc bẹt, điểm nằm bên trong góc.
Lời giải
a) Góc \(yOz\) là hình gồm hai tia chung gốc \(Oy\) và \(Oz\).
b) Góc bẹt là góc có hai tia đối nhau.
c) Khi hai tia \(Ox,Oy\) không đối nhau, \(M\) là điểm nằm trong góc \(xOy\) nếu tia \(OM\) nằm giữa hai tia \(Ox\) và \(Oy\).
Bài 2:
Cho ba điểm \(A,B,C\) không thẳng hàng. Kẻ các đường thẳng \(AB,AC,BC.\) Gọi \(M\) là điểm nằm trong góc \(ABC\) và góc \(ACB.\)
a) Chứng tỏ rằng \(M\) cũng nằm trong góc \(BAC.\)
b) Gọi \(I\) là giao điểm của hai đường thẳng \(AM\) và \(BC\). Hỏi điểm \(I\) nằm trong góc nào trong số các góc sau: \(\angle BAC,\angle BMC.\)
Phương pháp
Sử dụng kiến thức điểm nằm trong góc.
Lời giải
a) Điểm \(M\) nằm trong góc \(\angle ABC\) nên điểm \(M\) cùng phía với \(C\) so với \(AB\).
Điểm \(M\) nằm trong góc \(\angle ACB\) nên điểm \(M\) cùng phía với \(B\) so với \(AC\).
Từ đó, tia \(AM\) nằm giữa hai tia \(AB\) và \(AC\), nên điểm \(M\) nằm trong góc \(\angle BAC\).
b) \(I\) nằm trên tia \(AM\) nên tia \(AI\) nằm giữa hai tia \(AB\) và \(AC\). Do đó, điểm \(I\) nằm trong góc \(\angle BAC.\) Điểm \(I\) cũng nằm trong góc \(BMC.\)
Bài 3:
Cho hình vuông \(MNPQ\) và số đo các góc ghi tương ứng như hình sau:
a) Cho biết số đo của góc \(AMC\) bằng cách đo.
b) Sắp xếp góc góc \(NMA\), \(AMC\), \(CMQ\) theo thứ tự số đo tăng dần.

Phương pháp
a) Các bước đo:
Bước 1: Đặt thước đo góc để tâm thước trùng với đỉnh của góc cần đo
Bước 2: Vạch \({0^0}\) trên trước nằm trên một cạnh
Bước 3: Cạnh còn lại của góc đi qua vạch nào của thước đo góc thì đó là số đo của góc.
b) Sử dụng nhận xét để so sánh hai góc.
Lời giải
a) + Bước 1: Đặt thước đo góc để tâm thước trùng với điểm \(M\)
+ Bước 2: Vạch \({0^0}\) trên trước nằm trên cạnh \(MC\)
+ Bước 3: Cạnh \(MA\) của \(\angle AMC\) đi đến vạch số \({45^0}\) của thước đo góc
Vậy \(\angle AMC = {45^0}\)
b) Vì \({15^0} < {30^0} < {45^0}\) nên \(\angle NMA < \angle CMQ < \angle AMC\)
Sắp xếp góc góc theo thứ tự số đo tăng dần là: \(\angle NMA\); \(\angle CMQ\); \(\angle AMC\).













Danh sách bình luận