Đề ôn hè Toán 6 lên 7 - Đề 5

Đề bài

Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:

Câu 1: Số nào là đối của số –19?

A. –20.

B. 20.

C. 19.

D. –18.

Câu 2: Số -72 là bội của số nào sau đây?

A. -11.

B. 5.

C. 7.

D. –3.

Câu 3: Tập hợp tất cả các ước của -8 là:

A. {-1; -2; -4; -8}.

B. {1; 2; 4; 8; 0; -1; -2; -4; -8}.

C. {1; 2; 4; 8}.

D. {1; 2; 4; 8; -1; -2; -4; -8}.

Câu 4: Khẳng định nào sau đây là sai?

A. Trong hình thoi các góc đối không bằng nhau.

B. Hai góc kề một đáy của hình thang cân bằng nhau.

C. Trong hình chữ nhật hai đường chéo cắt nhau tại trung điểm của mỗi đường.

D. Hai đường chéo của hình vuông bằng nhau.

Câu 5: Trong các hình sau, hình ảnh nào có trục đối xứng:

A. Hình (1).

B. Hình (4).

C. Hình (3).

D. Hình (2).

Câu 6: Trong các hình sau, hình nào có tâm đối xứng.

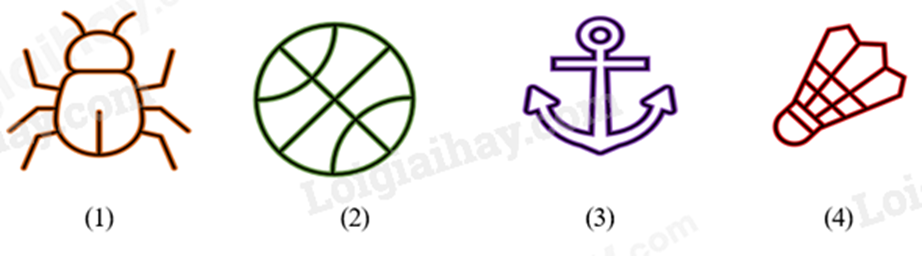
A. Hình (3).

B. Hình (1).

C. Hình (2).

D. Hình (4).

Câu 7: Liệt kê các con vật yêu thích ở trên cạn. Dãy dữ liệu mà các dữ liệu đều hợp lí là

A. Con chó, con lươn, con mèo.

B. Con chó, con mèo, con lợn, con gà.

C. Con mèo, con bạch tuộc, con rùa

D. Con chó, con mèo, con cá.

Câu 8: Tổng số gia cầm tại trang trại nhà bác Chi là \(150\) con. Số lượng mỗi loài được biểu diễn trong bảng sau:

Số  cần bổ sung vào bảng để biểu diễn số ngỗng là:

A. \(4\).

B. \(5\).

C. \(3\).

D. \(30\).

Câu 9: Ta có thể xem kim giờ và kim phút của đồng hồ là hai tia chung gốc (gốc trùng với trục quay của hai kim). Biết khi hai kim đồng hồ chỉ vào hai số liên tiếp nhau thì góc giữa hai kim đồng hồ là \(30^\circ \). Góc tạo bởi kim phút và kim giờ tại thời điểm \(7\)giờ là

A. \(70^\circ \).

B. \(30^\circ \).

C. \(180^\circ \).

D. \(150^\circ \).

Câu 10: Trong hình vẽ. Chọn khẳng định đúng

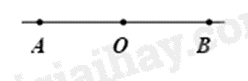
A. Hai tia AO và AB trùng nhau.

B. Hai tia OA và BO đối nhau.

C. Hai tia AO và OB đối nhau.

D. Hai tia BA và OB đối nhau.

Câu 11: Một hộp bút màu có nhiều màu: màu xanh, màu vàng, màu đỏ, màu đen, màu hồng, màu cam. Hỏi nếu rút bất kỳ một cây bút màu thì có thể xảy ra mấy kết quả?

A. 5.

B. 6.

C. 4.

D. 3.

Câu 12: Tung đồng xu 32 lần liên tiếp, có 18 lần xuất hiện mặt sấp thì xác suất thực nghiệm xuất hiện mặt ngửa là

A. \(\frac{7}{{16}}\).

B. \(\frac{3}{8}\).

C. \(\frac{{18}}{{32}}\).

D. \(\frac{{12}}{{32}}\).

Phần tự luận (7 điểm)

Bài 1. (1 điểm) Thực hiện phép tính (tính hợp lý nếu có thể)

a) \(100 + 2\left\{ {{3^2}.\left( { - 2} \right) - \left[ {10 + \left( { - 35} \right):\left( { - 5} \right)} \right]} \right\}\)

b) \(\frac{{ - 5}}{7}.\frac{2}{{11}} + \frac{{ - 5}}{7}.\frac{9}{{11}} + \frac{5}{7}\).

Bài 2. (1 điểm) Biểu đồ tranh dưới đây cho biết lượng sách giáo khoa lớp 6 - bộ Kết nối tri thức với cuộc sống, bán được tại một hiệu sách của ba mẹ bạn Nam vào ngày Chủ nhật vừa qua.

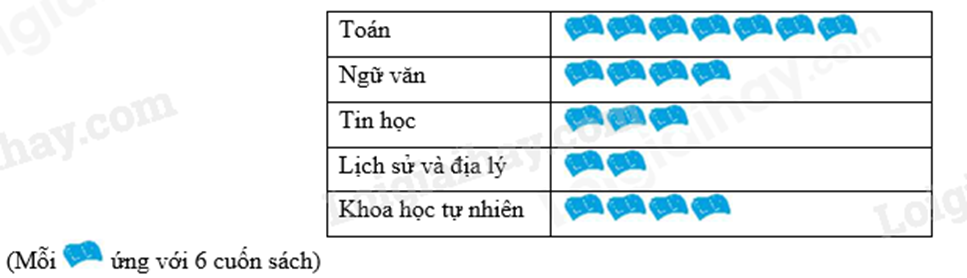
a) Tổng số sách giáo khoa lớp 6 mà hiệu sách bán được trong ngày chủ nhật vừa qua là bao nhiêu cuốn?

b) Lập bảng thống kê số sách lớp 6 bán được của hiệu sách? Sách nào bán nhiều nhất?

Bài 3. (1,5 điểm) Năm học 2023-2024, học sinh khối 6 của một trường THCS có từ 260 đến 310 học sinh. Trong buổi lễ chào cờ đầu tuần, xếp số học sinh đó thành hàng gồm 14 học sinh hay xếp thành hàng 21 học sinh thì không thừa học sinh nào. Hỏi tổng số học sinh của khối 6 là bao nhiêu?

Bài 4. (2,5 điểm)

1. Nền nhà của gia đình bạn Mai là hình chữ nhật có chiều dài 10m và chiều rộng bằng \(\frac{1}{2}\) chiều dài.

a) Tính diện tích nền nhà của gia đình bạn Mai?

b) Bố bạn Mai định dùng gạch men hình vuông có cạnh 50cm để lát kín nền căn phòng ấy. Hỏi cần bao nhiêu viên gạch như thế? (Biết rằng các mối nối và sự hao hụt không đáng kể).

2. Cho hai tia đối nhau Ox và Oy. Trên tia Ox lấy điểm A sao cho OA = 3 cm; trên tia Oy lấy điểm B sao cho OB = 4 cm.

a) Tính độ dài đoạn thẳng AB.

b) Xác định điểm M sao cho B là trung điểm của đoạn thẳng OM. Tính OM?

Bài 5. (1 điểm) a) Bạn An đọc một cuốn sách trong ba ngày. Ngày thứ nhất bạn An đọc được \(\frac{1}{4}\) số trang. Ngày thứ hai bạn An đọc được \(\frac{5}{9}\) số trang còn lại. Ngày thứ ba bạn An đọc nốt 80 trang còn lại. Cuốn sách bạn An đọc có bao nhiêu trang?

b) Cho \(A = \frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + \frac{1}{{{4^2}}} + ... + \frac{1}{{{{100}^2}}}\) . Chứng tỏ rằng \(A < \frac{3}{4}\).

-------- Hết --------

Lời giải

Phần trắc nghiệm

Câu 1: Số nào là đối của số –19?

A. –20.

B. 20.

C. 19.

D. –18.

Phương pháp

Số đối của số a là –a.

Lời giải

Số đối của số -19 là –(-19) = 19.

Đáp án: C.

Câu 2: Số -72 là bội của số nào sau đây?

A. -11.

B. 5.

C. 7.

D. –3.

Phương pháp

Để xét b có là bội của một số khác 0 hay không, ta chia b cho số đó. Nếu chia hết thì b là bội của số đó.

Lời giải

Ta có: \(\left( { - 72} \right) \vdots \left( { - 3} \right)\) nên -72 là bội của -3.

Đáp án: D.

Câu 3: Tập hợp tất cả các ước của -8 là:

A. {-1; -2; -4; -8}.

B. {1; 2; 4; 8; 0; -1; -2; -4; -8}.

C. {1; 2; 4; 8}.

D. {1; 2; 4; 8; -1; -2; -4; -8}.

Phương pháp

Cách tìm ước của một số a:

Kiểm tra trong các số tự nhiên từ 1 đến a, a chia hết cho những số nào thì những số đó là ước của a.

Lời giải

Tập hợp tất cả các ước của -8 là: {1; 2; 4; 8; -1; -2; -4; -8}.

Đáp án: D.

Câu 4: Khẳng định nào sau đây là sai?

A. Trong hình thoi các góc đối không bằng nhau.

B. Hai góc kề một đáy của hình thang cân bằng nhau.

C. Trong hình chữ nhật hai đường chéo cắt nhau tại trung điểm của mỗi đường.

D. Hai đường chéo của hình vuông bằng nhau.

Phương pháp

Dựa vào đặc điểm của các hình.

Lời giải

Trong hình thoi, các góc đối bằng nhau nên A sai.

Đáp án: A.

Câu 5: Trong các hình sau, hình ảnh nào có trục đối xứng:

A. Hình (1).

B. Hình (4).

C. Hình (3).

D. Hình (2).

Phương pháp

Xác định xem hình nào có trục đối xứng.

Trục đối xứng là đường thẳng chia hình thành hai phần mà khi ta “gấp” hình theo đường thẳng đó thì hai phần “chồng khít” lên nhau.

Lời giải

Hình (3) là hình có trục đối xứng.

Đáp án: C.

Câu 6: Trong các hình sau, hình nào có tâm đối xứng.

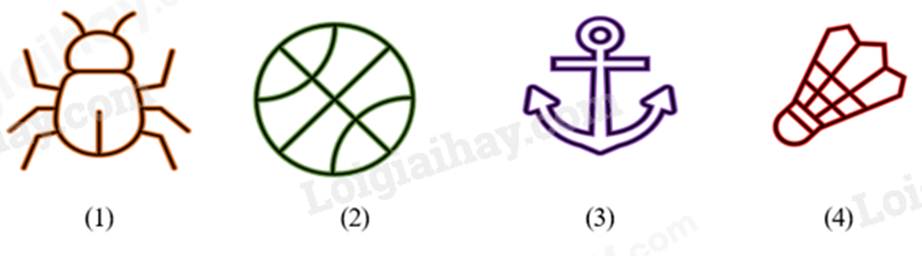
A. Hình (3).

B. Hình (1).

C. Hình (2).

D. Hình (4).

Phương pháp

Xác định hình có tâm đối xứng.

Tâm đối xứng là điểm sao cho khi quay nửa vòng quanh điểm điểm đó ta được vị trí mới của hình chồng khít với vị trí ban đầu (trước khi quay).

Lời giải

Hình (2) là hình có tâm đối xứng.

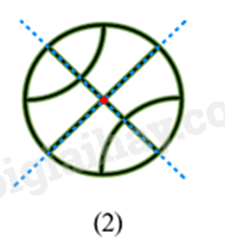
Đáp án: C.

Câu 7: Liệt kê các con vật yêu thích ở trên cạn. Dãy dữ liệu mà các dữ liệu đều hợp lí là

A. Con chó, con lươn, con mèo.

B. Con chó, con mèo, con lợn, con gà.

C. Con mèo, con bạch tuộc, con rùa

D. Con chó, con mèo, con cá.

Phương pháp

Xác định các con vật ở trên cạn.

Lời giải

Dãy dữ liệu mà các dữ liệu đều hợp lí là: “Con chó, con mèo, con lợn, con gà” vì các con vật này đều ở trên cạn.

Đáp án: B.

Câu 8: Tổng số gia cầm tại trang trại nhà bác Chi là \(150\) con. Số lượng mỗi loài được biểu diễn trong bảng sau:

Số  cần bổ sung vào bảng để biểu diễn số ngỗng là:

A. \(4\).

B. \(5\).

C. \(3\).

D. \(30\).

Phương pháp

Xác định số con gà, vịt, ngan.

Từ đó tính số con ngỗng.

Chuyển số con ngỗng thành biểu tượng.

Lời giải

Số con gà tại trang trại nhà bác Chi là: 10.5 = 50 (con)

Số con vịt tại trang trại nhà bác Chi là: 10.4 = 40 (con)

Số con ngan tại trang trại nhà bác Chi là: 10.3 = 30 (con)

Số con ngỗng tại trang trại nhà bác Chi là: 150 – 50 – 40 – 30 = 30 (con)

Số biểu tượng tương ứng với số con ngỗng là: 30 : 10 = 3 (biểu tượng)

Đáp án: C.

Câu 9: Ta có thể xem kim giờ và kim phút của đồng hồ là hai tia chung gốc (gốc trùng với trục quay của hai kim). Biết khi hai kim đồng hồ chỉ vào hai số liên tiếp nhau thì góc giữa hai kim đồng hồ là \(30^\circ \). Góc tạo bởi kim phút và kim giờ tại thời điểm \(7\)giờ là

A. \(70^\circ \).

B. \(30^\circ \).

C. \(180^\circ \).

D. \(150^\circ \).

Phương pháp

Xác định khoảng cách giữa số chỉ kim phút và kim giờ tại thời điểm 7 giờ.

Tính số đo góc = \(30^\circ \).

Lời giải

Tại thời điểm 7 giờ thì khoảng cách giữa kim phút và kim giờ là: 12 – 7 = 5.

Do đó góc tạo bởi kim giờ và kim phút là: \(30^\circ .5 = 150^\circ \).

Đáp án: D.

Câu 10: Trong hình vẽ. Chọn khẳng định đúng

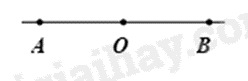
A. Hai tia AO và AB trùng nhau.

B. Hai tia OA và BO đối nhau.

C. Hai tia AO và OB đối nhau.

D. Hai tia BA và OB đối nhau.

Phương pháp

Hai tia đối nhau là hai tia chung gốc, tạo thành một đường thẳng.

Hai tia trùng nhau là hai tia chung gốc và cùng nằm 1 phía trên 1 đường thẳng.

Lời giải

Vì O nằm giữa A và B nên tia AO trùng với tia AB.

B, C, D các tia không chung gốc nên ta không xét thêm điều kiện.

Đáp án: A.

Câu 11: Một hộp bút màu có nhiều màu: màu xanh, màu vàng, màu đỏ, màu đen, màu hồng, màu cam. Hỏi nếu rút bất kỳ một cây bút màu thì có thể xảy ra mấy kết quả?

A. 5.

B. 6.

C. 4.

D. 3.

Phương pháp

Xác định các kết quả có thể xảy ra.

Lời giải

Các kết quả có thể xảy ra nếu rút bất kỳ một cây bút màu nào là: màu xanh, màu vàng, màu đỏ, màu đen, màu hồng, màu cam.

Vậy có 6 kết quả.

Đáp án: B.

Câu 12: Tung đồng xu 32 lần liên tiếp, có 18 lần xuất hiện mặt sấp thì xác suất thực nghiệm xuất hiện mặt ngửa là

A. \(\frac{7}{{16}}\).

B. \(\frac{3}{8}\).

C. \(\frac{{18}}{{32}}\).

D. \(\frac{{12}}{{32}}\).

Phương pháp

Cách tính xác suất thực nghiệm:

Bước 1: Xác định số lần được kết quả A (kết quả cần tính xác suất) và tổng số lần gieo.

Bước 2: Sử dụng công thức sau để tính xác suất: \(\frac{{n\left( A \right)}}{A}\) = Số lần sự kiện A xảy ra : Tổng số lần thực hiện hoạt động.

Lời giải

Số lần xuất hiện mặt ngửa là: \(32 - 18 = 14\) (lần)

Xác suất thực nghiệm xuất hiện mặt ngửa là: \(\frac{{14}}{{32}} = \frac{7}{{16}}\).

Đáp án: A.

Phần tự luận.

Bài 1. (1 điểm) Thực hiện phép tính (tính hợp lý nếu có thể)

a) \(100 + 2\left\{ {{3^2}.\left( { - 2} \right) - \left[ {10 + \left( { - 35} \right):\left( { - 5} \right)} \right]} \right\}\)

b) \(\frac{{ - 5}}{7}.\frac{2}{{11}} + \frac{{ - 5}}{7}.\frac{9}{{11}} + \frac{5}{7}\).

Phương pháp

a) Sử dụng quy tắc thực hiện phép tính theo đúng thứ tự.

b) Sử dụng tính chất phân phối của phép nhân với phép cộng.

Lời giải

a) \(100 + 2.\left\{ {{3^2}.( - 2) - [10 + ( - 35):( - 5)]} \right\}\)

\(\begin{array}{l} = 100 + 2.\left\{ {9.( - 2) - [10 + 7]} \right\}\\ = 100 + 2.( - 18 - 17)\\ = 100 + 2.( - 35)\\ = 100 - 70\\ = 30\end{array}\)

b) \(\frac{{ - 5}}{7} \cdot \frac{2}{{11}} + \frac{{ - 5}}{7} \cdot \frac{9}{{11}} + \frac{5}{7}\)

\( = \frac{{ - 5}}{7}.\left( {\frac{2}{{11}} + \frac{9}{{11}} - 1} \right)\)

\( = \frac{{ - 5}}{7}.0 = 0\)

Bài 2. (1 điểm) Biểu đồ tranh dưới đây cho biết lượng sách giáo khoa lớp 6 - bộ Kết nối tri thức với cuộc sống, bán được tại một hiệu sách của ba mẹ bạn Nam vào ngày Chủ nhật vừa qua.

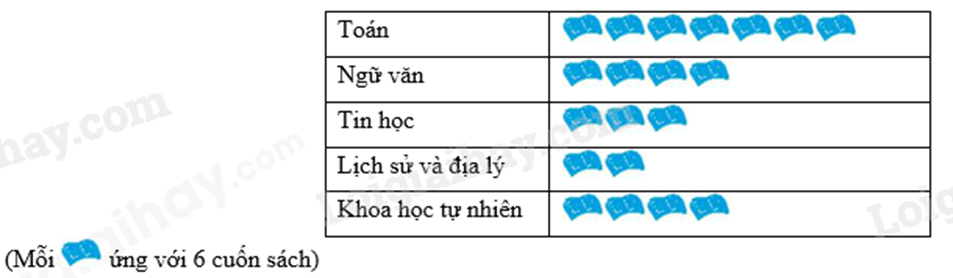
a) Tổng số sách giáo khoa lớp 6 mà hiệu sách bán được trong ngày chủ nhật vừa qua là bao nhiêu cuốn?

b) Lập bảng thống kê số sách lớp 6 bán được của hiệu sách? Sách nào bán nhiều nhất?

Phương pháp

a) Tổng số sách giáo khoa = tổng số biểu tượng . 6.

b) Tính số lượng sách mỗi loại bán được rồi lập bảng thống kê.

Lời giải

b) Số cuốn sách Toán bán được là: 7.6 = 42 (cuốn)

Số cuốn sách Ngữ văn bán được là: 4.6 = 24 (cuốn)

Số cuốn sách Tin học bán được là: 3.6 = 18 (cuốn)

Số cuốn sách LS và ĐL là: 2.6 = 12 (cuốn)

Số cuốn sách KHTN là: 4.6 = 24 (cuốn)

Ta có bảng thống kê sau:

Sách Toán bán nhiều nhất (42 cuốn)

Bài 3. (1,5 điểm) Năm học 2023-2024, học sinh khối 6 của một trường THCS có từ 260 đến 310 học sinh. Trong buổi lễ chào cờ đầu tuần, xếp số học sinh đó thành hàng gồm 14 học sinh hay xếp thành hàng 21 học sinh thì không thừa học sinh nào. Hỏi tổng số học sinh của khối 6 là bao nhiêu?

Phương pháp

Gọi số học sinh khối 6 là a (a \( \in \) N).

Theo bài ta có: a\( \vdots \)14; a\( \vdots \)21 và 260 < a < 310

Phân tích số 14 và 21 để tìm BCNN(14;21)

Từ đó tìm BC(14;21) thông qua BCNN(14;21)

Kết hợp điều kiện 260 < a < 310 suy ra số học sinh khối 6.

Lời giải

Gọi số học sinh khối 6 là a (a \( \in \) N).

Ta có: a\( \vdots \)14; a\( \vdots \)21 và 260 < a < 310

a\( \in \)BC(14,21)

Ta có: 14 = 2.7; 21 = 3.7

Suy ra BCNN(14,21) = 2.3.7 = 42

Do đó BC(14;21) = B(42) = \(\left\{ {0;42;84;126;168;210;252;294;336;...} \right\}\)

Mà 260 < a < 310 nên a = 294

Vậy số học sinh khối 6 là 294 học sinh.

Bài 4. (2,5 điểm)

1. Nền nhà của gia đình bạn Mai là hình chữ nhật có chiều dài 10m và chiều rộng bằng \(\frac{1}{2}\) chiều dài.

a) Tính diện tích nền nhà của gia đình bạn Mai?

b) Bố bạn Mai định dùng gạch men hình vuông có cạnh 50cm để lát kín nền căn phòng ấy. Hỏi cần bao nhiêu viên gạch như thế? (Biết rằng các mối nối và sự hao hụt không đáng kể).

2. Cho hai tia đối nhau Ox và Oy. Trên tia Ox lấy điểm A sao cho OA = 3 cm; trên tia Oy lấy điểm B sao cho OB = 4 cm.

a) Tính độ dài đoạn thẳng AB.

b) Xác định điểm M sao cho B là trung điểm của đoạn thẳng OM. Tính OM?

Phương pháp

1. a) Tính chiều rộng theo chiều dài.

Diện tích nền nhà = chiều rộng.chiều dài.

b) Tính diện tích một viên gạch hình vuông = cạnh . cạnh.

Số viên gạch = diện tích nền nhà : diện tích một viên gạch (diện tích cần đưa về cùng đơn vị trước khi chia).

2. Vì điểm O nằm giữa A và B nên:

AB = OA + OB

b) Để B là trung điểm của OM thì B nằm giữa O, M và \(MB = OB = \frac{{OM}}{2}\) nên ta tính độ dài OM theo OB.

Lời giải

1.

a) Chiều rộng nền phòng là: \(\frac{1}{2}.10 = 5\;\left( m \right)\)

Diện tích nền nhà của gia định bạn Mai là: 5.10 = 50 (\({m^2}\))

b) Diện tích một viên gạch là: \(50.50 = 2500{\rm{c}}{{\rm{m}}^2} = 0,25{\rm{\;}}{{\rm{m}}^2}\)

Số viên gạch để lát kín nền căn phòng là: \(50:0,25 = 200{\rm{\;}}\left( {{\rm{vi\^e n}}} \right)\)

2.

a)

Vì điểm O nằm giữa A và B nên:

AB = OA + OB = 3 + 4 = 7 (cm)

b) Để B là trung điểm của OM thì B nằm giữa O, M và \(MB = OB = \frac{{OM}}{2}\).

Suy ra OM = OB.2 = 4.2 = 8cm.

Vậy M thuộc tia OB sao cho OM = 8cm thì B là trung điểm của đoạn thẳng OM.

Bài 5. (1 điểm) a) Bạn An đọc một cuốn sách trong ba ngày. Ngày thứ nhất bạn An đọc được \(\frac{1}{4}\) số trang. Ngày thứ hai bạn An đọc được \(\frac{5}{9}\) số trang còn lại. Ngày thứ ba bạn An đọc nốt 80 trang còn lại. Cuốn sách bạn An đọc có bao nhiêu trang?

b) Cho \(A = \frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + \frac{1}{{{4^2}}} + ... + \frac{1}{{{{100}^2}}}\) . Chứng tỏ rằng \(A < \frac{3}{4}\) .

Phương pháp

a) Xác định phân số ứng với 80 trang.

Tính số trang sau ngày thứ nhất.

Xác định phân số ứng với số trang còn lại sau ngày thứ nhất.

Tính số trang của quyển sách.

b) Chứng minh \(A < \frac{1}{4} + \frac{1}{{2.3}} + \frac{1}{{3.4}} + ... + \frac{1}{{99.100}}\).

Biến đổi \(\frac{1}{{k.\left( {k + 1} \right)}} = \frac{1}{k} - \frac{1}{{k + 1}}\), rút gọn vế phải để chứng minh \(A < \frac{3}{4}\).

Lời giải

a) Theo đề bài, 80 trang sách chiếm \(1 - \frac{5}{9} = \frac{4}{9}\) (số trang còn lại sau ngày thứ nhất).

Số trang còn lại sau ngày thứ nhất là: \(80:\frac{4}{9} = 180\) (trang)

Số trang còn lại sau ngày thứ nhất chiếm \(1 - \frac{1}{4} = \frac{3}{4}\) (tổng số trang).

Quyển sách bạn An đọc có tổng số trang là: \(180:\frac{3}{4} = 240\)(trang)

Vậy quyển sách bạn An đọc có 240 trang.

b) Ta có: \(A = \frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + \frac{1}{{{4^2}}} + ... + \frac{1}{{{{100}^2}}}\)

\(A = \frac{1}{4} + \frac{1}{{3.3}} + \frac{1}{{4.4}} + ... + \frac{1}{{100.100}} < \frac{1}{4} + \frac{1}{{2.3}} + \frac{1}{{3.4}} + ... + \frac{1}{{99.100}}\)

\(\begin{array}{l}A < \frac{1}{4} + \frac{1}{2} - \frac{1}{3} + \frac{1}{3} - \frac{1}{4} + ... + \frac{1}{{99}} - \frac{1}{{100}} = \frac{1}{4} + \frac{1}{2} - \frac{1}{{100}}\\A < \frac{3}{4} - \frac{1}{{100}} < \frac{3}{4}\end{array}\)