Đề ôn hè Toán 6 lên 7 - Đề 1

Đề bài

Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:

Câu 1: Biểu thức nào là phân số?

A. \(\frac{{ - 4}}{{ - 9}}\).

B. \(\frac{1}{0}\).

C. \(\frac{{12}}{{8,5}}\).

D. \(\frac{{3,2}}{6}\).

Câu 2: Kết quả của phép tính \({2^{10}}:{2^5}\) là

A. \({1^5}\).

B. \({2^5}\).

C. \({2^2}\).

D. \({1^2}\).

Câu 3: Mức tiêu thụ nhiên liệu của một chiếc xe máy là 1,6 lít xăng trên 100km. Tại thời điểm xăng có giá 26471 đồng/lít, xe máy đó đi quãng đường 50km thì tiêu thụ hết bao nhiêu tiền xăng (kết quả làm tròn đến hàng đơn vị)?

A. 21 176,8 đồng.

B. 21 177 đồng.

C. 26 471 đồng.

D. 21 176 đồng.

Câu 4: Một bạn tung đồng xu 20 lần liên tiếp thì thấy có 6 lần xuất hiện mặt sấp. Xác suất thực nghiệm xuất hiện mặt ngửa là:

A. \(\frac{{10}}{3}\).

B. \(\frac{{10}}{7}\).

C. \(\frac{3}{{10}}\).

D. \(\frac{7}{{10}}\).

Câu 5: Một lớp 42 học sinh gồm 24 học sinh nam, còn lại là học sinh nữ. Tỉ số giữa số học sinh nữ với số học sinh nam trong lớp là

A. \(\frac{4}{7}\;\).

B. \(\frac{3}{4}\;\).

C. \(\frac{3}{7}\;\).

D. \(\frac{4}{3}\;\).

Câu 6: Biết 75%  của một sợi dây là 9 mét thì sợi dây có chiều dài là

A. \(6,75\;\) mét.

B. \(12\) mét.

C. \(5,41\) mét.

D. \(6,85\) mét.

Câu 7: Kết quả bài kiểm tra học kì II môn Toán lớp 6A được biểu diễn bằng biểu đồ sau:

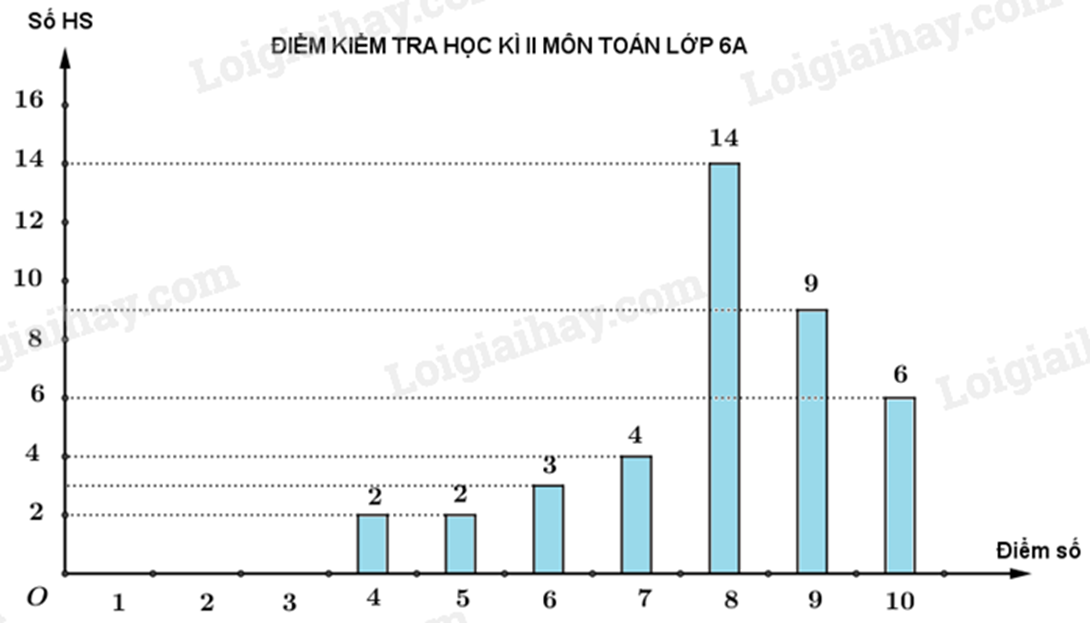
Số học sinh đạt được 9 điểm và 10 điểm môn Toán của lớp 6A là

A. 10.

B. 15.

C. 19.

D. 6.

Câu 8: Trong các hình sau, hình nào chỉ có hai trục đối xứng?

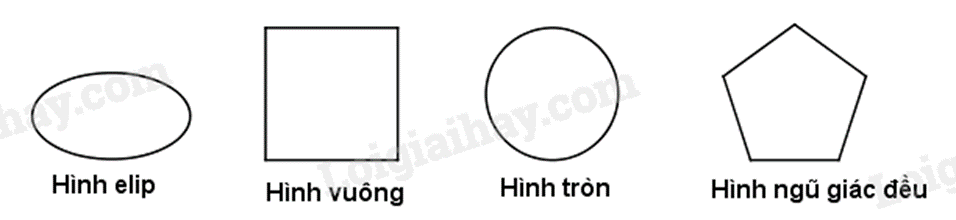
A. Hình tròn.

B. Hình ngũ giác đều.

C. Hình elip.

D. Hình vuông.

Câu 9: Nếu cùng tăng chiều dài và chiều rộng của một hình chữ nhật lên bốn lần thì ta được một hình chữ nhật mới có diện tích bằng bao nhiêu lần diện tích hình chữ nhật ban đầu?

A. 16 lần.

B. 64 lần.

C. 4 lần.

D. 8 lần.

Câu 10: Cho góc \(xOy\) bằng \(100^\circ \) thì góc \(xOy\) là

A. góc nhọn.

B. góc vuông.

C. góc tù.

D. góc bẹt.

Câu 11: Trong hình vẽ sau, khẳng định sai là

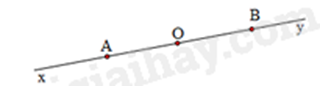
A. Hai tia BO và By đối nhau.

B. Hai tia AO và OB trùng nhau.

C. Hai tia AO và AB trùng nhau.

D. Hai tia Ax và AB đối nhau.

Câu 12: Cho đoạn thẳng CD dài 4cm và M là trung điểm của đoạn thẳng CD. Độ dài đoạn thẳng CM bằng

A. 4cm.

B. 2cm.

C. 8cm.

D. 16cm.

Phần tự luận (7 điểm)

Bài 1. (2 điểm) Thực hiện phép tính (tính hợp lí nếu có thể)

a) \(\frac{{ - 1}}{4} + \frac{3}{5}\)

b) \(\,\frac{3}{5}.\frac{1}{3} + \frac{4}{5}\)

c) \(\,\frac{5}{{19}}.\frac{8}{{15}} + \frac{5}{{19}}.\frac{{17}}{{15}} - \frac{5}{{19}}.\frac{6}{{15}}\)

d) \(\frac{{ - 3}}{7}.\frac{4}{9} + \frac{{ - 3}}{7}.\frac{5}{9} + \frac{{ - 4}}{7}\)

Bài 2. (1,5 điểm)

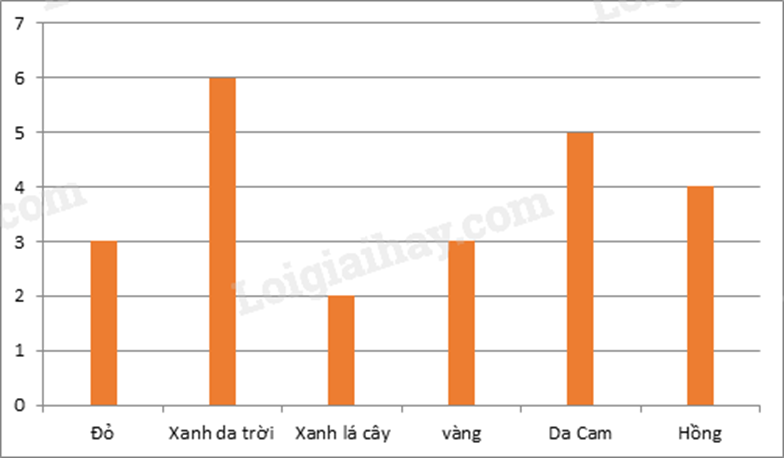
Biểu đồ trên cho biết màu sắc yêu thích nhất của một nhóm học sinh.

a) Những màu nào được yêu thích nhiều hơn màu đỏ?

b) Màu nào được nhiều bạn yêu thích nhất?

c) Lập bảng thống kê số lượng học sinh yêu thích của mỗi màu?

Bài 3. (1 điểm) Một sân trường hình chữ nhật có chiều rộng 60m, chiều dài bằng \(\frac{5}{4}\) chiều rộng. Người ta dùng 12% diện tích sân trường để trồng hoa và cây xanh. Tính diện tích phần đất còn lại của sân trường.

Bài 4. (2 điểm) Cho điểm O nằm trên đường thẳng xy. Trên tia Oy lấy hai điểm A và B sao cho OA = 3cm, OB = 5cm.

a) Tính độ dài đoạn thẳng AB.

b) Lấy điểm C thuộc tia Ox sao cho AC = 6cm. Chứng minh O là trung điểm của đoạn thẳng AC.

Bài 5. (0,5 điểm) Tìm x, biết: \(\frac{1}{{5.8}} + \frac{1}{{8.11}} + \frac{1}{{11.14}} +  \cdots  + \frac{1}{{x\left( {x + 3} \right)}} = \frac{{101}}{{1540}}\).

-------- Hết --------

Lời giải

Phần trắc nghiệm

Câu 1: Biểu thức nào là phân số?

A. \(\frac{{ - 4}}{{ - 9}}\).

B. \(\frac{1}{0}\).

C. \(\frac{{12}}{{8,5}}\).

D. \(\frac{{3,2}}{6}\).

Phương pháp

Phân số có dạng \(\frac{a}{b}\) (\(a,b \in \mathbb{Z},b \ne 0\)).

Lời giải

Trong các biểu thức trên, chỉ có \(\frac{{ - 4}}{{ - 9}}\) là phân số.

\(\frac{1}{0}\) không phải phân số vì có mẫu số bằng 0.

\(\frac{{12}}{{8,5}};\frac{{3,2}}{6}\) không phải phân số vì \(8,5;3,2\) không phải số nguyên.

Đáp án: A.

Câu 2: Kết quả của phép tính \({2^{10}}:{2^5}\) là

A. \({1^5}\).

B. \({2^5}\).

C. \({2^2}\).

D. \({1^2}\).

Phương pháp

Sử dụng quy tắc chia hai luỹ thừa cùng cơ số: \({a^m}:{a^n} = {a^{m - n}}\left( {a \ne 0;m \ge n} \right)\)

Lời giải

Ta có: \({2^{10}}:{2^5} = {2^{10 - 5}} = {2^5}\).

Đáp án: B.

Câu 3: Mức tiêu thụ nhiên liệu của một chiếc xe máy là 1,6 lít xăng trên 100km. Tại thời điểm xăng có giá 26471 đồng/lít, xe máy đó đi quãng đường 50km thì tiêu thụ hết bao nhiêu tiền xăng (kết quả làm tròn đến hàng đơn vị)?

A. 21 176,8 đồng.

B. 21 177 đồng.

C. 26 471 đồng.

D. 21 176 đồng.

Phương pháp

Tính số lít xăng tiêu thụ.

Tính số tiền xăng.

Lời giải

Số lít xăng mà xe máy tiêu thụ khi đi quãng đường 50km là: \(1,6:100.50 = 0,8\) (lít)

Khi đó số tiền xăng là: \(26\,471.0,8 = 21\,176,8\) (đồng)

Làm tròn đến hàng đơn vị, ta được 21 177 đồng.

Đáp án: B.

Câu 4: Một bạn tung đồng xu 20 lần liên tiếp thì thấy có 6 lần xuất hiện mặt sấp. Xác suất thực nghiệm xuất hiện mặt ngửa là:

A. \(\frac{{10}}{3}\).

B. \(\frac{{10}}{7}\).

C. \(\frac{3}{{10}}\).

D. \(\frac{7}{{10}}\).

Phương pháp

Tính số lần xuất hiện mặt ngửa.

Xác suất thực nghiệm xuất hiện mặt ngửa = số lần xuất hiện mặt ngửa : tổng số lần tung.

Lời giải

Số lần xuất hiện mặt ngửa là: 20 – 6 = 14 (lần)

Xác suất thực nghiệm xuất hiện mặt ngửa là: \(\frac{{14}}{{20}} = \frac{7}{{10}}\).

Đáp án: D.

Câu 5: Một lớp 42 học sinh gồm 24 học sinh nam, còn lại là học sinh nữ. Tỉ số giữa số học sinh nữ với số học sinh nam trong lớp là

A. \(\frac{4}{7}\;\).

B. \(\frac{3}{4}\;\).

C. \(\frac{3}{7}\;\).

D. \(\frac{4}{3}\;\).

Phương pháp

Tính số học sinh nữ.

Tính tỉ số số học sinh nữ với số học sinh nam = số học sinh nữ : số học sinh nam.

Lời giải

Số học sinh nữ là: 42 – 24 = 18 (học sinh)

Tỉ số giữa số học sinh nữ với số học sinh nam trong lớp là: 18 : 24 = \(\frac{3}{4}\).

Đáp án: B.

Câu 6: Biết 75% của một sợi dây là 9 mét thì sợi dây có chiều dài là

A. \(6,75\;\) mét.

B. \(12\) mét.

C. \(5,41\) mét.

D. \(6,85\) mét.

Phương pháp

Sử dụng công thức tìm một số a khi biết \(m\% \) của a bằng b thì \(a = b:\frac{m}{{100}}\).

Lời giải

Sợi dây có chiều dài là: \(9:\frac{{75}}{{100}} = 12\) (mét)

Đáp án: B.

Câu 7: Kết quả bài kiểm tra học kì II môn Toán lớp 6A được biểu diễn bằng biểu đồ sau:

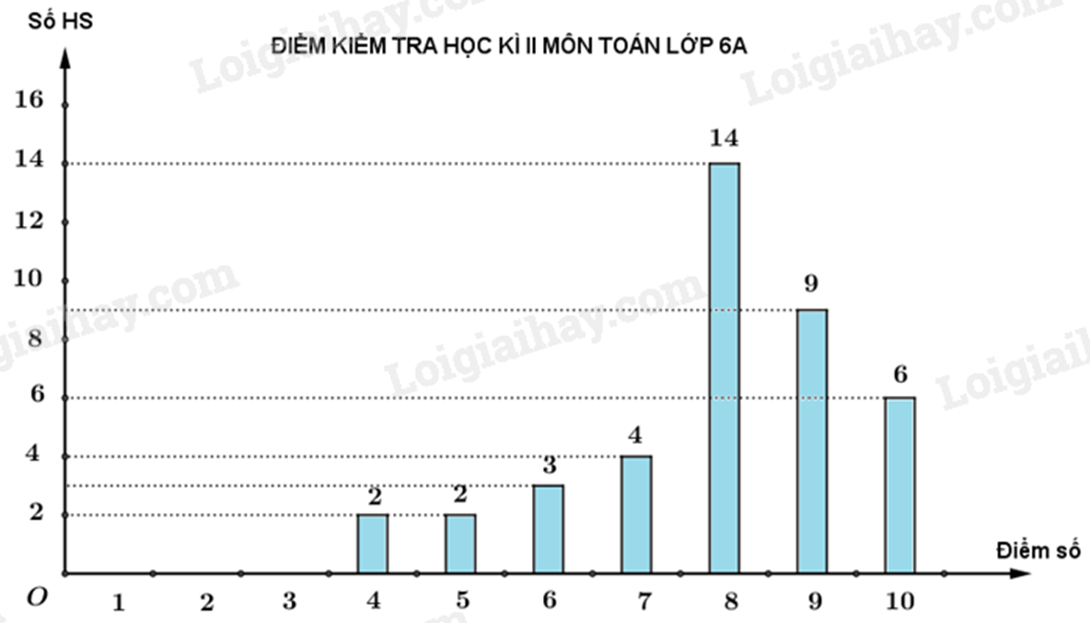
Số học sinh đạt được 9 điểm và 10 điểm môn Toán của lớp 6A là

A. 10.

B. 15.

C. 19.

D. 6.

Phương pháp

Quan sát biểu đồ, xác định số học sinh đạt điểm 9, điểm 10. Tính tổng số học sinh đó.

Lời giải

Số học sinh đạt điểm 9 là: 9 học sinh; đạt điểm 10 là: 6 học sinh.

Số học sinh đạt được 9 điểm và 10 điểm môn Toán của lớp 6A là: 9 + 6 = 15 (học sinh)

Đáp án: B.

Câu 8: Trong các hình sau, hình nào chỉ có hai trục đối xứng?

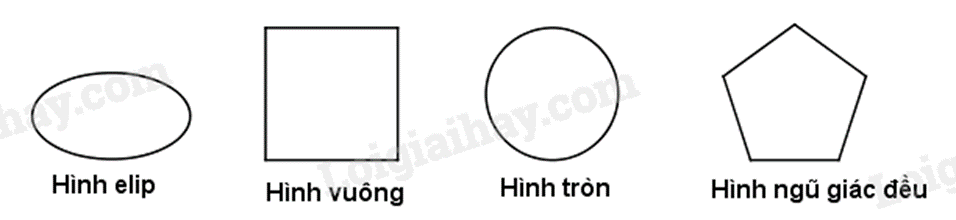
A. Hình tròn.

B. Hình ngũ giác đều.

C. Hình elip.

D. Hình vuông.

Phương pháp

Xác định trục đối xứng của các hình trên.

Lời giải

Hình elip có hai trục đối xứng:

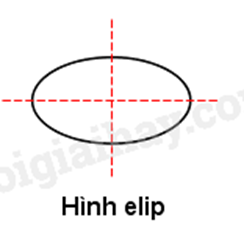
Hình vuông có 4 trục đối xứng:

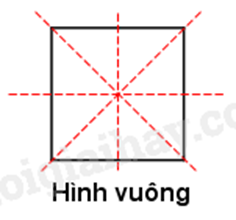
Hình tròn có vô số trục đối xứng:

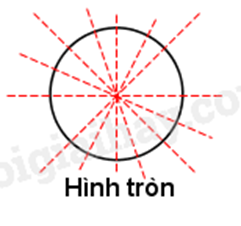
Hình ngũ giác đều có 5 trục đối xứng.

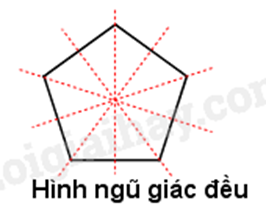
Đáp án: C.

Câu 9: Nếu cùng tăng chiều dài và chiều rộng của một hình chữ nhật lên bốn lần thì ta được một hình chữ nhật mới có diện tích bằng bao nhiêu lần diện tích hình chữ nhật ban đầu?

A. 16 lần.

B. 64 lần.

C. 4 lần.

D. 8 lần.

Phương pháp

Sử dụng công thức tính diện tích hình chữ nhật: S = chiều dài . chiều rộng

Lời giải

Cách 1. Diện tích hình chữ nhật mới gấp diện tích hình chữ nhật cũ là: \(4.4 = 16\) (lần)

Cách 2. Gọi chiều dài và chiều rộng hình chữ nhật ban đầu là a, b.

Diện tích ban đầu là: a.b.

Chiều dài và chiều rộng hình chữ nhật sau khi tăng lên 4 lần là 4a, 4b.

Diện tích hình chữ nhật mới là: 4a.4b = 16ab.

Diện tích hình chữ nhật mới gấp diện tích hình chữ nhật cũ là: 16ab : ab = 16 (lần)

Đáp án: A.

Câu 10: Cho góc \(xOy\) bằng \(100^\circ \) thì góc \(xOy\) là

A. góc nhọn.

B. góc vuông.

C. góc tù.

D. góc bẹt.

Phương pháp

+ Góc nhọn là góc số góc có số đo lớn hơn \(0^\circ \) và nhỏ hơn \(90^\circ \).

+ Góc vuông là góc có số đo bằng \(90^\circ \).

+ Góc tù là góc có số đo lớn hơn \(90^\circ \) và nhỏ hơn \(180^\circ \).

+ Góc bẹt là góc có số đo bằng  \(180^\circ \).

Lời giải

Vì \(\widehat {xOy} = 100^\circ  > 90^\circ \) nên \(\widehat {xOy}\) là góc tù.

Đáp án: C.

Câu 11: Trong hình vẽ sau, khẳng định sai là

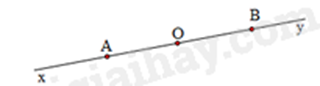
A. Hai tia BO và By đối nhau.

B. Hai tia AO và OB trùng nhau.

C. Hai tia AO và AB trùng nhau.

D. Hai tia Ax và AB đối nhau.

Phương pháp

Hai tia chung gốc Ox và Oy tạo thành một đường thẳng xy gọi là hai tia đối nhau.

Hai tia trùng nhau là hai tia chung gốc và cùng nằm 1 phía trên 1 đường thẳng

Lời giải

Hai tia BO và By có chung gốc O và tạo nên đường thẳng Oy nên là hai tia đối nhau. Đáp án A đúng.

Hai tia AO và OB không có chung gốc nên không trùng nhau. Đáp án B sai.

Hai tia AO và AB có chung gốc A và O, B cùng nằm một phía nên hai tia AO và AB trùng nhau. Đáp án C đúng,

Hai tia Ax và AB có chung gốc A và tạo nên đường thẳng Bx nên là hai tia đối nhau. Đáp án D đúng.

Vậy ta chọn đáp án B.

Đáp án: B.

Câu 12: Cho đoạn thẳng CD dài 4cm và M là trung điểm của đoạn thẳng CD. Độ dài đoạn thẳng CM bằng

A. 4cm.

B. 2cm.

C. 8cm.

D. 16cm.

Phương pháp

Trung điểm của đoạn thẳng chia đoạn thẳng thành hai phần bằng nhau và bằng một nửa đoạn thẳng đó.

Lời giải

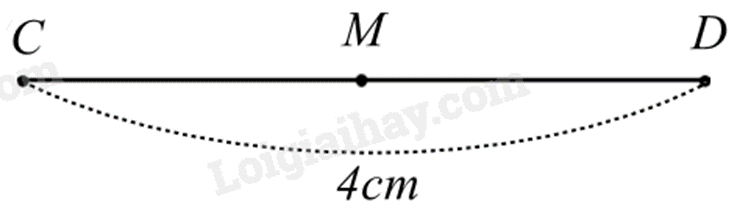
Vì M là trung điểm của CD nên CM = MD = \(\frac{{CD}}{2} = \frac{4}{2} = 2\left( {cm} \right)\)

Đáp án: B.

Phần tự luận.

Bài 1. (2 điểm) Thực hiện phép tính (tính hợp lí nếu có thể)

a) \(\frac{{ - 1}}{4} + \frac{3}{5}\)

b) \(\,\frac{3}{5}.\frac{1}{3} + \frac{4}{5}\)

c) \(\,\frac{5}{{19}}.\frac{8}{{15}} + \frac{5}{{19}}.\frac{{17}}{{15}} - \frac{5}{{19}}.\frac{6}{{15}}\)

d) \(\frac{{ - 3}}{7}.\frac{4}{9} + \frac{{ - 3}}{7}.\frac{5}{9} + \frac{{ - 4}}{7}\)

Phương pháp

Sử dụng kết hợp quy tắc cộng, trừ, nhân chia phân số và tính chất của các phép tính.

Lời giải

a) \(\frac{{ - 1}}{4} + \frac{3}{5} = \frac{{ - 5}}{{20}} + \frac{{12}}{{20}} = \frac{7}{{20}}\).

b) \(\,\frac{3}{5}.\frac{1}{3} + \frac{4}{5} = \frac{1}{5} + \frac{4}{5} = 1\)

c) \(\,\frac{5}{{19}}.\frac{8}{{15}} + \frac{5}{{19}}.\frac{{17}}{{15}} - \frac{5}{{19}}.\frac{6}{{15}}\)

\(\begin{array}{l} = \frac{5}{{19}}\left( {\frac{8}{{15}} + \frac{{17}}{{15}} - \frac{6}{{15}}} \right)\\ = \frac{5}{{19}}.\frac{{19}}{{15}}\\ = \frac{5}{{15}}\\ = \frac{1}{3}\end{array}\)

d) \(\frac{{ - 3}}{7}.\frac{4}{9} + \frac{{ - 3}}{7}.\frac{5}{9} + \frac{{ - 4}}{7}\)

\(\begin{array}{l} = \frac{{ - 3}}{7}.\left( {\frac{4}{9} + \frac{5}{9}} \right) + \frac{{ - 4}}{7}\\ = \frac{{ - 3}}{7}.1 + \frac{{ - 4}}{7}\\ = \frac{{ - 3}}{7} + \frac{{ - 4}}{7}\\ =  - 1\end{array}\)

Bài 2. (1,5 điểm)

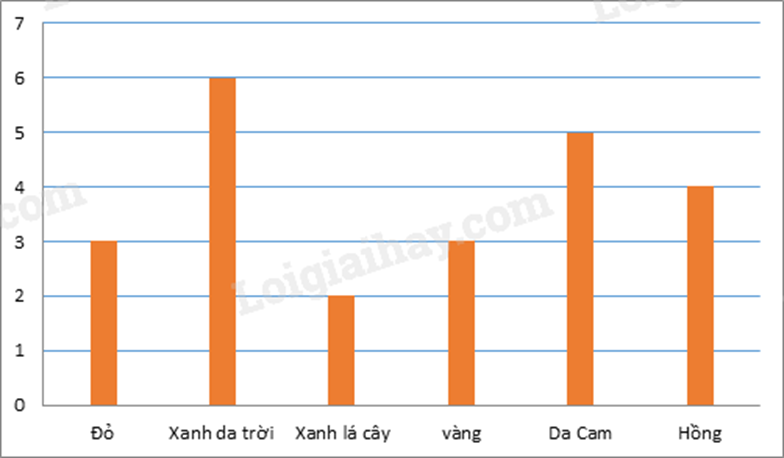
Biểu đồ trên cho biết màu sắc yêu thích nhất của một nhóm học sinh.

a) Những màu nào được yêu thích nhiều hơn màu đỏ?

b) Màu nào được nhiều bạn yêu thích nhất?

c) Lập bảng thống kê số lượng học sinh yêu thích của mỗi màu?

Phương pháp

a) Quan sát biểu đồ để xác định số học sinh yêu thích các màu. So sánh với số học sinh yêu thích màu đỏ.

b) So sánh số học sinh yêu thích các màu, xác định số lớn nhất ứng với màu được nhiều bạn yêu thích nhất.

c) Dựa vào số học sinh yêu thích, ta có bảng thuống kê gồm hai dòng: màu sắc, số lượng.

Lời giải

a) Quan sát biểu đồ, ta thấy số học sinh yêu thích:

+ màu đỏ: 3 học sinh.

+ màu xanh da trời: 6 học sinh.

+ màu xanh lá cây: 2 học sinh.

+ màu vàng: 3 học sinh.

+ màu da cam: 5 học sinh.

+ màu hồng: 4 học sinh.

Do đó những màu được yêu thích nhiều hơn màu đỏ là: xanh da trời, da cam, hồng.

b) Vì 6 là số lớn nhất nên màu được nhiều bạn yêu thích nhất là màu xanh da trời.

c) Dựa vào số học sinh yêu thích, ta có bảng thuống kê sau:

Bài 3. (1 điểm) Một sân trường hình chữ nhật có chiều rộng 60m, chiều dài bằng \(\frac{5}{4}\) chiều rộng. Người ta dùng 12% diện tích sân trường để trồng hoa và cây xanh. Tính diện tích phần đất còn lại của sân trường.

Phương pháp

Tính chiều dài sân trường = chiều rộng.\(\frac{5}{4}\).

Tính diện tích của sân trường: S_{hình chữ nhật} = chiều dài. chiều rộng.

Diện tích trồng hoa và cây xanh = diện tích sân trường.\(\frac{{12}}{{100}}\).

Diện tích đất còn lại = diện tích sân trường – diện tích trồng hoa và cây xanh.

Lời giải

Chiều dài sân trường là: \(60.\frac{5}{4} = 75\left( m \right)\)

Diện tích của sân trường là: \(75.60 = 4500\left( {{m^2}} \right)\)

Diện tích trồng hoa và cây xanh là: \(4500.\frac{{12}}{{100}} = 540\left( {{m^2}} \right)\)

Diện tích phần đất còn lại của sân trường là: \(4500 - 540 = 3960\left( {{m^2}} \right)\)

Vậy diện tích phần đất còn lại của sân trường là \(3960{m^2}\).

Bài 4. (2 điểm) Cho điểm O nằm trên đường thẳng xy. Trên tia Oy lấy hai điểm A và B sao cho OA = 3cm, OB = 5cm.

a) Tính độ dài đoạn thẳng AB.

b) Lấy điểm C thuộc tia Ox sao cho AC = 6cm. Chứng minh O là trung điểm của đoạn thẳng AC.

Phương pháp

a) Chứng minh A nằm giữa O và B.

Từ đó tính độ dài AB = OB – OA.

b) Chứng minh O nằm giữa A và C. Từ đó tính độ dài OC = AC – OA.

Chứng minh OA = OC.

Suy ra O là trung điểm của AC.

Lời giải

a) Vì A, B cùng phía so với O, lại có OA = 3cm < OB = 5cm nên A nằm giữa O và B.

Ta có: AB = OB – OA = 5 – 3 = 2 (cm).

Vậy AB = 2cm.

b) Vì C thuộc tia Ox. Mà Ox là tia đối của tia Oy nên O nằm giữa A và C.

Ta có: OC = AC – OA = 6 – 3 = 3 (cm).

Suy ra OA = OC = 3cm.

Vậy O là trung điểm của AC.

Bài 5. (0,5 điểm) Tìm x, biết: \(\frac{1}{{5.8}} + \frac{1}{{8.11}} + \frac{1}{{11.14}} +  \cdots  + \frac{1}{{x\left( {x + 3} \right)}} = \frac{{101}}{{1540}}\).

Phương pháp

Sử dụng công thức: \(\frac{k}{{n\left( {n + k} \right)}} = \frac{{n + k - n}}{{n\left( {n + k} \right)}} = \frac{1}{n} - \frac{1}{{n + k}}\).

- Nhân cả hai vế với 3 để đưa các phân số vế trái thành dạng \(\frac{3}{{n\left( {n + 3} \right)}}\)

Khi đó \(\frac{3}{{n\left( {n + 3} \right)}} = \frac{{n + 3 - n}}{{n\left( {n + 3} \right)}} = \frac{1}{n} - \frac{1}{{n + 3}}\).

- Rút gọn vế trái để tìm x.

Lời giải

Ta có: \(\frac{1}{{5.8}} + \frac{1}{{8.11}} + \frac{1}{{11.14}} +  \cdots  + \frac{1}{{x\left( {x + 3} \right)}} = \frac{{101}}{{1540}}\)

Nhân cả 2 vế với 3, ta được:

\(\frac{3}{{5.8}} + \frac{3}{{8.11}} + \frac{3}{{11.14}} +  \cdots  + \frac{3}{{x\left( {x + 3} \right)}} = \frac{{101.3}}{{1540}}\)

\(\frac{1}{5} - \frac{1}{8} + \frac{1}{8} - \frac{1}{{11}} + \frac{1}{{11}} - \frac{1}{{14}} +  \cdots  + \frac{1}{x} - \frac{1}{{x + 3}} = \frac{{303}}{{1540}}\)

\(\frac{1}{5} - \frac{1}{{x + 3}} = \frac{{303}}{{1540}}\)

\(\frac{1}{{x + 3}} = \frac{1}{{308}}\)

\(x = 305\)

Vậy \(x = 305\).