Đề ôn hè Toán 6 lên 7 - Đề 7

Đề bài

Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:

Câu 1: Cho tập hợp \(H = \left\{ {1;2;5;8;9} \right\}\). Phát biểu nào sau đây đúng?

A. \(3 \in H\).

B. \(5 \notin H\).

C. \(8 \in H\).

D. \(H = \left\{ {5;8;9} \right\}\).

Câu 2: Số đối của số 9 là số nào trong các đáp án dưới đây?

A. 9.

B. \(\frac{1}{9}\).

C. -9.

D. \( - \frac{1}{9}\).

Câu 3: Kết quả của phép tính \(\left( { - 89} \right) + 27\) là:

A. 62.

B. -62.

C. 116.

D. -116.

Câu 4: Tập hợp tất cả các ước của -8 là:

A. \(\left\{ {1;2;4;8} \right\}\).

B. \(\left\{ { - 1; - 2; - 4; - 8} \right\}\).

C. \(\left\{ { - 8; - 1;1;8} \right\}\).

D. \(\left\{ { - 8; - 4; - 2; - 1;1;2;4;8} \right\}\).

Câu 5: Trong các hình sau đây, hình nào là hình thoi:

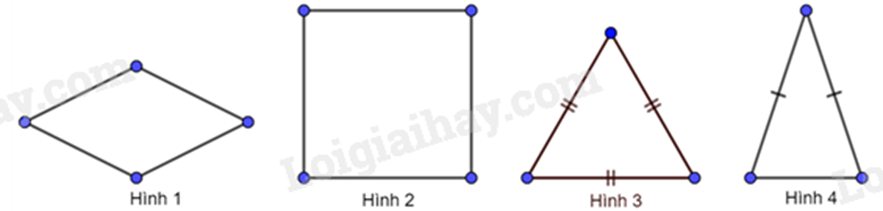
A. Hình 1.

B. Hình 2.

C. Hình 3.

D. Hình 4.

Câu 6: Chữ cái nào sau đây có cả trục đối xứng và tâm đối xứng ?

A. W.

B. X.

C. Y.

D. Z.

Câu 7: Kết quả khi rút gọn phân số \(\frac{{20}}{{ - 140}}\) đến tối giản là:

A. \( - \frac{{10}}{{70}}\).

B. \( - \frac{4}{{28}}\).

C. \( - \frac{2}{{14}}\).

D. \( - \frac{1}{7}\).

Câu 8: Tính 25% của 12 bằng

A. 2.

B. 3.

C. 4.

D. 6.

Câu 9: Làm tròn số a = 135,4956 đến chữ số thập phân thứ hai ta được số thập phân nào sau đây:

A. 135,49.

B. 135,51.

C. 135,50.

D. 136.

Câu 10: Dữ liệu nào sau đây là dữ liệu số?

A. Bảng danh sách học tên học sinh lớp 6A1.

B. Tên các tỉnh phía Bắc.

C. Bảng điểm tổng kết học kì I môn toán lớp 6A1.

D. Tên các lớp trong trường.

Câu 11: Tung \(1\) đồng xu hai mặt N và S cân đối và đồng chất \(20\)lần. Có \(8\) lần xuất hiện mặt N thì xác suất thực nghiệm xuất hiện mặt N là bao nhiêu?

A. 8.

B. \(\frac{2}{5}\).

C. 20.

D. \(\frac{{12}}{{20}}\).

Câu 12: Góc có số đo bằng \(60^\circ \) là

A. góc nhọn.

B. góc vuông.

C. góc tù.

D. góc bẹt.

Phần tự luận (7 điểm)

Bài 1. (1 điểm) Thực hiện phép tính (tính nhanh nếu có thể):

a) \(\frac{{ - 1}}{2} + \frac{1}{4}:\frac{3}{4}\);

b) \(\left( {1\frac{3}{4} - \frac{7}{{15}}} \right) - \left( {\frac{3}{4} - \frac{{23}}{{24}} + \frac{8}{{15}}} \right)\).

Bài 2. (1 điểm) Tìm x, biết:

a) \(x + \frac{1}{5} = \frac{3}{5}\);

b) \(\frac{1}{9} + {\left( {x - \frac{1}{3}} \right)^2} = \frac{5}{9}\).

Bài 3. (1 điểm) Với tinh thần “Tương thân tương ái”, nhà trường đã phát động học sinh quyên góp sách giáo khoa ủng hộ các bạn học sinh vùng cao. Kết quả số sách thu được trong khoảng từ 1000 đến 1300 cuốn. Biết rằng nếu xếp số sách thành từng bó, mỗi bó 20, 25 hay 30 cuốn đều vừa đủ. Tính số sách nhà trường đã quyên góp được.

Bài 4. (1 điểm) Bạn Nam gieo một con xúc xắc 30 lần và ghi lại số chấm xuất hiện ở mỗi lần gieo được kết quả như sau:

a) Lập bảng thống kê theo mẫu sau:

b) Tính xác suất thực nghiệm của sự kiện số chấm xuất hiện là số lẻ.

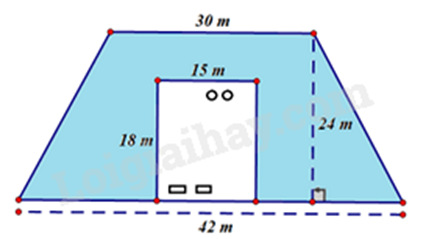
Bài 5. (1,5 điểm) Một khu đất hình chữ nhật (dùng để làm nhà) được bao quanh bởi vườn hoa có hình thang cân với các kích thước như hình vẽ.

a) Tính diện tích khu đất dùng để làm nhà?

b) Nếu mỗi túi hạt giống hoa gieo vừa đủ trên \(33{m^2}\) đất; mỗi túi hạt giống giá 15 000 đồng (mười lăm nghìn đồng) thì cần bao nhiêu tiền để mua hạt giống hoa gieo vừa đủ khu đất đó?

Bài 6. (1,5 điểm) Trên tia Ox lấy hai điểm A, B sao cho OA = 4cm, OB = 6cm. Gọi C là trung điểm của đoạn thẳng OA.

a) Tính độ dài đoạn thẳng AB.

b) Điểm A có là trung điểm của đoạn thẳng BC không? Vì sao?

c) Lấy điểm D nằm ngoài đường thẳng AB. Vẽ các tia DO, DC, DA, DB. Em hãy viết tên các góc đỉnh D có trong hình vẽ.

-------- Hết --------

Lời giải

Phần trắc nghiệm

Câu 1: Cho tập hợp \(H = \left\{ {1;2;5;8;9} \right\}\). Phát biểu nào sau đây đúng?

A. \(3 \in H\).

B. \(5 \notin H\).

C. \(8 \in H\).

D. \(H = \left\{ {5;8;9} \right\}\).

Phương pháp

\( \in \): thuộc

\( \notin \): không thuộc.

Lời giải

Vì \(8 \in H\) nên C đúng.

Đáp án: C.

Câu 2: Số đối của số 9 là số nào trong các đáp án dưới đây?

A. 9.

B. \(\frac{1}{9}\).

C. -9.

D. \( - \frac{1}{9}\).

Phương pháp

Số đối của \(a\) là \( - a\).

Lời giải

Số đối của số 9 là -9.

Đáp án: C.

Câu 3: Kết quả của phép tính \(\left( { - 89} \right) + 27\) là:

A. 62.

B. -62.

C. 116.

D. -116.

Phương pháp

Để cộng hai số nguyên khác dấu, ta làm như sau:

Bước 1: Bỏ dấu “-” trước số nguyên âm, giữ nguyên số còn lại.

Bước 2. Trong hai số nguyên dương nhận được ở Bước 1, ta lấy số lớn hơn trừ đi số nhỏ hơn.

Bước 3. Cho hiệu vừa nhận được dấu ban đầu của số lớn hơn ở Bước 2, ta có tổng cần tìm.

Lời giải

Ta có:

\(\begin{array}{l}\left( { - 89} \right) + 27\\ =  - \left( {89 - 27} \right)\\ =  - 62\end{array}\)

Đáp án: B.

Câu 4: Tập hợp tất cả các ước của -8 là:

A. \(\left\{ {1;2;4;8} \right\}\).

B. \(\left\{ { - 1; - 2; - 4; - 8} \right\}\).

C. \(\left\{ { - 8; - 1;1;8} \right\}\).

D. \(\left\{ { - 8; - 4; - 2; - 1;1;2;4;8} \right\}\).

Phương pháp

Để tìm ước của -8, ta tìm các số mà khi chia -8 cho chúng đều ra kết quả là số nguyên.

Lời giải

Tập hợp tất cả các ước của -8 là \(\left\{ { - 8; - 4; - 2; - 1;1;2;4;8} \right\}\).

Đáp án: D.

Câu 5: Trong các hình sau đây, hình nào là hình thoi:

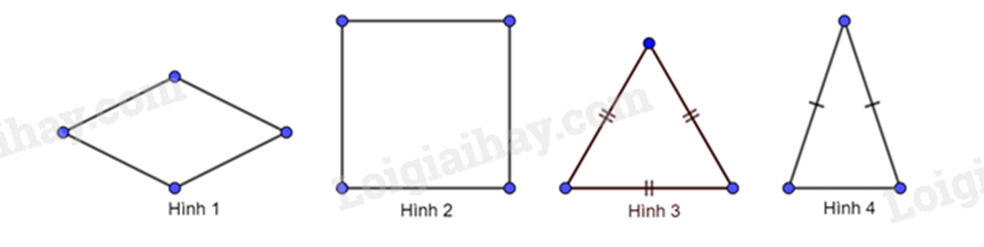
A. Hình 1.

B. Hình 2.

C. Hình 3.

D. Hình 4.

Phương pháp

Dựa vào đặc điểm của hình thoi:

- Bốn cạnh bằng nhau.

- Hai đường chéo vuông góc với nhau.

- Các cạnh đối song song với nhau.

- Các góc đối bằng nhau.

Lời giải

Hình thoi là hình 1.

Đáp án: A.

Câu 6: Chữ cái nào sau đây có cả trục đối xứng và tâm đối xứng ?

A. W.

B. X.

C. Y.

D. Z.

Phương pháp

Trục đối xứng là đường thẳng chia hình thành hai phần mà khi ta “gấp” hình theo đường thẳng đó thì hai phần “chồng khít” lên nhau.

Tâm đối xứng là điểm sao cho khi quay nửa vòng quanh điểm điểm đó ta được vị trí mới của hình chồng khít với vị trí ban đầu (trước khi quay).

Lời giải

Hình có tâm đối xứng, trục đối xứng trong các hình trên là X.

Đáp án: B.

Câu 7: Kết quả khi rút gọn phân số \(\frac{{20}}{{ - 140}}\) đến tối giản là:

A. \( - \frac{{10}}{{70}}\).

B. \( - \frac{4}{{28}}\).

C. \( - \frac{2}{{14}}\).

D. \( - \frac{1}{7}\).

Phương pháp

Tìm ƯCLN của tử và mẫu rồi chia cả tử và mẫu cho ƯCLN đó.

Lời giải

Ta có: \(\left( { - 140} \right) \vdots 20\) nên ƯCLN(20;-140) = 20.

Do đó \(\frac{{20}}{{ - 140}} =  - \frac{{20}}{{140}} =  - \frac{1}{7}\).

Đáp án: D.

Câu 8: Tính 25% của 12 bằng

A. 2.

B. 3.

C. 4.

D. 6.

Phương pháp

Tính \(m\% \) của a bằng \(a.\frac{m}{{100}}\).

Lời giải

25% của 12 là: \(12.\frac{{25}}{{100}} = 3\).

Đáp án: B.

Câu 9: Làm tròn số a = 135,4956 đến chữ số thập phân thứ hai ta được số thập phân nào sau đây:

A. 135,49.

B. 135,51.

C. 135,50.

D. 136.

Phương pháp

Để làm tròn số thập phân dương tới một hàng nào đó (gọi là hàng làm tròn), ta làm như sau:

- Đối với chữ số hàng làm tròn:

    + Giữ nguyên nếu chữ số ngay bên phải nhỏ hơn 5;

    + Tăng 1 đơn vị nếu chữ số ngay bên phải lớn hơn hoặc bằng 5

- Đối với chữ số sau hàng làm tròn:

    + Bỏ đi nếu ở phần thập phân;

    + Thay bằng các chữ số 0 nếu ở phần số nguyên.

Lời giải

Chữ số thập phân thứ 2 là 9.

Chữ số ngay bên phải là 5 nên ta tăng chữ số 9 lên một đơn vị (các chữ số tính từ hàng cao nhất đến chữ số thập phân thứ hai là 135,49 cộng thêm một đơn vị ở chữ số thập phân thứ hai là 135,50) và bỏ các chữ số từ chữ số thập phân thứ ba trở đi.

Do đó số a = 135,4956 làm tròn đến chữ số thập phân thứ hai ta được số thập phân 135,50.

Đáp án: C.

Câu 10: Dữ liệu nào sau đây là dữ liệu số?

A. Bảng danh sách học tên học sinh lớp 6A1.

B. Tên các tỉnh phía Bắc.

C. Bảng điểm tổng kết học kì I môn toán lớp 6A1.

D. Tên các lớp trong trường.

Phương pháp

Dữ liệu số được biểu diễn bởi số.

Lời giải

Bảng danh sách học tên học sinh lớp 6A1 được biểu diễn bằng chữ (ví dụ: Nguyễn Văn A,…).

Tên các tỉnh phía Bắc được biểu diễn bằng chữ (ví dụ: Bắc Ninh,...).

Bảng điểm tổng kết học kì I môn toán lớp 6A1 được biểu diễn bằng số (ví dụ: 6,4; 8,2,...).

Tên các lớp trong trường thường được biểu diễn bởi cả số và chữ (ví dụ: 6A, 6B, 6A1,…).

Đáp án: C.

Câu 11: Tung \(1\) đồng xu hai mặt N và S cân đối và đồng chất \(20\)lần. Có \(8\) lần xuất hiện mặt N thì xác suất thực nghiệm xuất hiện mặt N là bao nhiêu?

A. 8.

B. \(\frac{2}{5}\).

C. 20.

D. \(\frac{{12}}{{20}}\).

Phương pháp

Cách tính xác suất thực nghiệm:

Bước 1: Xác định số lần được kết quả A (kết quả cần tính xác suất) và tổng số lần gieo.

Bước 2: Sử dụng công thức sau để tính xác suất: \(\frac{{n\left( A \right)}}{A}\) = Số lần sự kiện A xảy ra : Tổng số lần thực hiện hoạt động.

Lời giải

Xác suất thực nghiệm xuất hiện mặt N là: \(\frac{8}{{20}} = \frac{2}{5}\).

Đáp án: B.

Câu 12: Góc có số đo bằng \(60^\circ \) là

A. góc nhọn.

B. góc vuông.

C. góc tù.

D. góc bẹt.

Phương pháp

Góc nhọn là góc có số đo nhỏ hơn \(90^\circ \).

Góc vuông là góc có số đo bằng \(90^\circ \).

Góc tù là góc có số đo lớn hơn \(90^\circ \).

Góc bẹt là góc có số đo bằng \(180^\circ \).

Lời giải

Vì \(60^\circ  < 90^\circ \) nên góc \(60^\circ \) là góc nhọn.

Đáp án: A.

Phần tự luận.

Bài 1. (1 điểm) Thực hiện phép tính (tính nhanh nếu có thể):

a) \(\frac{{ - 1}}{2} + \frac{1}{4}:\frac{3}{4}\);

b) \(\left( {1\frac{3}{4} - \frac{7}{{15}}} \right) - \left( {\frac{3}{4} - \frac{{23}}{{24}} + \frac{8}{{15}}} \right)\).

Phương pháp

a) Thực hiện lần lượt phép nhân rồi đến phép cộng phân số.

b) Phá ngoặc, sử dụng tính chất kết hợp để nhóm các phân số cùng mẫu rồi tính.

Lời giải

a) \(\frac{{ - 1}}{2} + \frac{1}{4}:\frac{3}{4}\)

\( = \frac{{ - 1}}{2} + \frac{1}{4}.\frac{4}{3}\)

\( = \frac{{ - 1}}{2} + \frac{1}{3}\)

\( = \frac{{ - 1}}{6}\)

b) \(\left( {1\frac{3}{4} - \frac{7}{{15}}} \right) - \left( {\frac{3}{4} - \frac{{23}}{{24}} + \frac{8}{{15}}} \right)\)

\( = 1\frac{3}{4} - \frac{7}{{15}} - \frac{3}{4} + \frac{{23}}{{24}} - \frac{8}{{15}}\)

\( = \left( {1\frac{3}{4} - \frac{3}{4}} \right) - \left( {\frac{7}{{15}} + \frac{8}{{15}}} \right) + \frac{{23}}{{24}}\)

\( = 1 - 1 + \frac{{23}}{{24}}\)

\( = \frac{{23}}{{24}}\)

Bài 2. (1 điểm) Tìm , biết:

a) \(x + \frac{1}{5} = \frac{3}{5}\);

b) \(\frac{1}{9} + {\left( {x - \frac{1}{3}} \right)^2} = \frac{5}{9}\).

Phương pháp

a) Sử dụng quy tắc chuyển vế để tìm \(x\).

b) Sử dụng quy tắc chuyển vế.

Nếu \({A^2} = {B^2}\) thì \(A = B\) hoặc \(A =  - B\).

Lời giải

a) \(x + \frac{1}{5} = \frac{3}{5}\)

\(\begin{array}{l}x = \frac{3}{5} - \frac{1}{5}\\x = \frac{2}{5}\end{array}\)

Vậy \(x = \frac{2}{5}\)

b) \(\frac{1}{9} + {\left( {x - \frac{1}{3}} \right)^2} = \frac{5}{9}\)

\(\begin{array}{l}{\left( {x - \frac{1}{3}} \right)^2} = \frac{5}{9} - \frac{1}{9}\\{\left( {x - \frac{1}{3}} \right)^2} = \frac{4}{9}\\{\left( {x - \frac{1}{3}} \right)^2} = {\left( {\frac{{ \pm 2}}{3}} \right)^2}\end{array}\)

Suy ra \(x - \frac{1}{3} = \frac{2}{3}\) hoặc \(x - \frac{1}{3} = \frac{{ - 2}}{3}\)

* TH1: \(x - \frac{1}{3} = \frac{2}{3}\)

suy ra \(x = \frac{2}{3} + \frac{1}{3} = 1\)

* TH2: \(x - \frac{1}{3} = \frac{{ - 2}}{3}\)

suy ra \(x = \frac{{ - 2}}{3} + \frac{1}{3} = \frac{{ - 1}}{3}\)

Vậy \(x \in \left\{ {1;\frac{{ - 1}}{3}} \right\}\)

Bài 3. (1 điểm) Với tinh thần “Tương thân tương ái”, nhà trường đã phát động học sinh quyên góp sách giáo khoa ủng hộ các bạn học sinh vùng cao. Kết quả số sách thu được trong khoảng từ 1000 đến 1300 cuốn. Biết rằng nếu xếp số sách thành từng bó, mỗi bó 20, 25 hay 30 cuốn đều vừa đủ. Tính số sách nhà trường đã quyên góp được.

Phương pháp

Gọi số sách nhà trường đã quyên góp được là a (quyển; \(a \in N*;1000\; \le a \le \;1300\)).

Theo đề bài suy ra \(a \in BC\left( {20,25,30} \right)\)

Phân tích 20; 25 và 30 để tìm BCNN(20;25;30)

Suy ra BC(20;25;30) = B(BCNN(20;25;30))

Kết hợp điều kiện suy ra giá trị của a.

Lời giải

Gọi số sách nhà trường đã quyên góp được là a (quyển; \(a \in N*;1000\; \le a \le \;1300\)).

Theo đề bài ta có: a\( \vdots \)20 ; a\( \vdots \)25; a\( \vdots \)30. Suy ra: \(a \in BC\left( {20,25,30} \right)\)

Ta có:

20 = \({2^2}.5\)

25 = \({5^2}\)

30 = 2.3.5

BCNN(20;25;30) = \({2^2}{.3.5^2}\) = 300

BC(20;25;30) = B(300) = {0; 300; 600; 900; 1200; 1800; …}

Mà \(a \in BC\left( {20,25,30} \right);1000\; \le a \le \;1300\) nên a = 1200

Vậy số sách nhà trường đã quyên góp được là 1200 quyển.

Bài 4. (1 điểm) Bạn Nam gieo một con xúc xắc 30 lần và ghi lại số chấm xuất hiện ở mỗi lần gieo được kết quả như sau:

a) Lập bảng thống kê theo mẫu sau:

b) Tính xác suất thực nghiệm của sự kiện số chấm xuất hiện là số lẻ.

Phương pháp

a) Từ dãy số liệu, lập bảng thống kê.

b) Cách tính xác suất thực nghiệm:

Bước 1: Xác định số lần được kết quả A (kết quả cần tính xác suất) và tổng số lần gieo.

Bước 2: Sử dụng công thức sau để tính xác suất: \(\frac{{n\left( A \right)}}{A}\) = Số lần sự kiện A xảy ra : Tổng số lần thực hiện hoạt động.

Lời giải

a)

b) Xác suất thực nghiệm của sự kiện số chấm xuất hiện là số lẻ là: \(\frac{{6 + 7 + 5}}{{30}} = 0,6\).

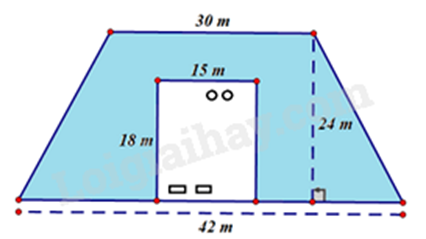
Bài 5. (1,5 điểm) Một khu đất hình chữ nhật (dùng để làm nhà) được bao quanh bởi vườn hoa có hình thang cân với các kích thước như hình vẽ.

a) Tính diện tích khu đất dùng để làm nhà?

b) Nếu mỗi túi hạt giống hoa gieo vừa đủ trên \(33{m^2}\) đất; mỗi túi hạt giống giá 15 000 đồng (mười lăm nghìn đồng) thì cần bao nhiêu tiền để mua hạt giống hoa gieo vừa đủ khu đất đó?

Phương pháp

a) Sử dụng công thức tính diện tích hình chữ nhật = chiều rộng.chiều dài.

b) Tính diện tích vườn hoa = diện tích hình thang – diện tích khu đất.

Tính số túi hạt giống = diện tích vườn hoa : diện  tích gieo của mỗi túi hạt giống.

Số tiền = giá một túi hạt giống . số túi hạt giống.

Lời giải

a) Diện tích khu đất dùng để làm nhà là: \(15.18 = 270({m^2})\)

b) Diện tích vườn hoa là: \((30 + 42).24:2 - 270 = 594({m^2})\)

Cần số túi hạt giống hoa là: \(594:33 = 18\)(túi)

Cần số tiền mua hạt giống hoa là: \(18.15000 = 270000\) (đồng)

Bài 6. (1,5 điểm) Trên tia Ox lấy hai điểm A, B sao cho OA = 4cm, OB = 6cm. Gọi C là trung điểm của đoạn thẳng OA.

a) Tính độ dài đoạn thẳng AB.

b) Điểm A có là trung điểm của đoạn thẳng BC không? Vì sao?

c) Lấy điểm D nằm ngoài đường thẳng AB. Vẽ các tia DO, DC, DA, DB. Em hãy viết tên các góc đỉnh D có trong hình vẽ.

Phương pháp

a) Chỉ ra A nằm giữa O và B nên tính được AB theo OA và OB.

b) Nếu A có nằm giữa B và C và AC = AB thì A là trung điểm của BC.

c) Xác định các góc đỉnh D dựa vào hình vẽ.

Lời giải

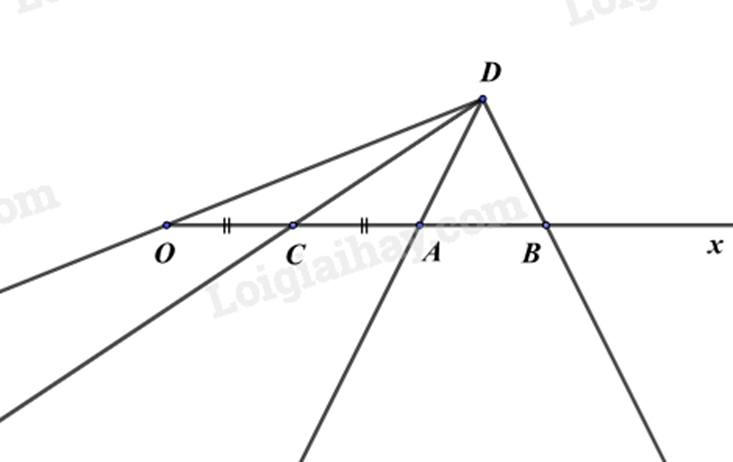
a) Vì A, B thuộc tia Ox và OA < OB (4cm < 6cm) nên A nằm giữa O và B.

Do đó: AB = OB - OA = 6 - 4 = 2cm

Vậy AB = 2cm

b) Vì C là trung điểm của đoạn thẳng OA nên \(AC = \frac{{OA}}{2} = \frac{4}{2} = 2\left( {cm} \right)\)

Mà AB = 2cm nên AC = AB

Lại có A nằm giữa B và C

Suy ra A là trung điểm của đoạn thẳng BC

Vậy A là trung điểm của đoạn thẳng BC

c) Các góc đỉnh D có trong hình vẽ là: \(\widehat {ODC};\widehat {ODA};\widehat {ODB};\widehat {CDA};\widehat {CDB};\widehat {ADB}\).