Đề ôn hè Toán 6 lên 7 - Đề 6

Đề bài

Câu 1. (1,5 điểm) Tính nhanh (nếu có thể): 

a) \(\frac{5}{{12}} + \frac{{ - 17}}{{12}}\)

b) \(( - 13,2) + ( - 0,8):2\)

c) \(\frac{{21}}{{37}}.\frac{1}{{25}} + \frac{1}{{25}}.\frac{{16}}{{37}} - \frac{1}{{25}}\) 

Câu 2. (1 điểm) Tìm \(x\) biết: 

a) \(\frac{4}{5} = \frac{{ - 12}}{{9 - x}}\)

b) \(x + 2,5 = 4.25\% \)

Câu 3. (3 điểm)

1. Lớp 6A có 40 học sinh, số học sinh giỏi chiếm 20%  số học sinh cả lớp. Số học sinh khá bằng \(\frac{3}{2}\) số học sinh giỏi, còn lại là học sinh trung bình. Tính số học sinh mỗi loại.

2. Kết thúc học kì I năm học 2022-2023, số học sinh giỏi của các lớp 6A, 6B, 6C, 6D của một trường THCS lần lượt là: 18; 20; 22; 16 (học sinh).

a) Lập bảng thống kê số học sinh giỏi của các lớp 6.

b) Vẽ biểu đồ cột biểu diễn bảng thống kê ở câu a.

3. Một chiếc thùng kín đựng một số quả bóng màu đỏ, màu xanh, màu vàng có cùng kích thước. Trong một trò chơi, người chơi lấy ngẫu nhiên một quả bóng, ghi lại màu rồi trả lại bóng vào thùng.

a) Quả bóng lấy ra có thể có màu gì?

b) Bình thực hiện trò chơi 20 lần và được kết quả như bảng sau:

Tính xác suất thực nghiệm của sự kiện quả bóng lấy ra có màu vàng.

Câu 4. (1,5 điểm) Một căn phòng hội trường có nền nhà là hình chữ nhật với chiều dài 14m và chiều rộng 12m. Người ta dự định dùng loại gạch hình vuông có kích thước cạnh 40cm để lát nền đó.

a) Tính diện tích nền nhà hình chữ nhật và diện tích của viên gạch hình vuông.

b) Giả sử một viên gạch để lát sàn là 30 000 đồng, chi phí tiền công lát và các vật liệu khác là 70 000 đồng/m\(^2\). Để lát kín nền nhà bằng loại gạch trên thì người ta phải trả tất cả khoảng bao nhiêu đồng (làm tròn kết quả đến hàng triệu)? Biết rằng các viên gạch được lát liền nhau, coi mạch vữa giữa các viên gạch không đáng kể.

Câu 5. (2,5 điểm) Cho đoạn thẳng AB = 5cm. Lấy điểm C thuộc đoạn thẳng AB sao cho AC = 1cm.

a) Tính độ dài đoạn thẳng CB.

b) Gọi D là trung điểm của đoạn thẳng CB, tính độ dài đoạn thẳng CD?

c) Vẽ tia Ax là tia đối của tia AB. Lấy điểm E thuộc tia Ax sao cho AE = 3cm. Điểm A có là trung điểm của đoạn thẳng ED? Vì sao?

d) Vẽ tia Ay sao cho \(\widehat {BAy} = 60^\circ \). So sánh góc BAy và góc BAx.

Câu 6. (0,5 điểm) Cho  M = \(\frac{1}{{{2^3}}}\) + \(\frac{2}{{{3^3}}}\) + \(\frac{3}{{{4^3}}}\)+ .....+ \(\frac{{2021}}{{{{2022}^3}}}\)+ \(\frac{{2022}}{{{{2023}^3}}}\). Chứng tỏ rằng giá trị của M không phải là một số tự nhiên.

-------- Hết --------

Lời giải

Câu 1. (1,5 điểm) Tính nhanh (nếu có thể): 

a) \(\frac{5}{{12}} + \frac{{ - 17}}{{12}}\)

b) \(( - 13,2) + ( - 0,8):2\)

c) \(\frac{{21}}{{37}}.\frac{1}{{25}} + \frac{1}{{25}}.\frac{{16}}{{37}} - \frac{1}{{25}}\) 

Phương pháp

Sử dụng quy tắc cộng, trừ, nhân, chia với phân số, số thập phân.

Lời giải

a) \(\frac{5}{{12}} + \frac{{ - 17}}{{12}} = \frac{{ - 12}}{{12}} =  - 1\)

b) \(( - 13,2) + ( - 0,8):2\)

\( = ( - 13,2) + ( - 0,4) =  - 13,6\)

c) \(\frac{{21}}{{37}}.\frac{1}{{25}} + \frac{1}{{25}}.\frac{{16}}{{37}} - \frac{1}{{25}}\)

\( = \frac{1}{{25}}\left( {\frac{{21}}{{37}} + \frac{{16}}{{37}} - 1} \right)\)

\( = \frac{1}{{25}}.\left( {1 - 1} \right) = \frac{1}{{25}}.0 = 0\)

Câu 2. (1 điểm) Tìm \(x\) biết: 

a) \(\frac{4}{5} = \frac{{ - 12}}{{9 - x}}\)

b) \(x + 2,5 = 4.25\% \)

Phương pháp

a) Sử dụng tính chất: \(\frac{a}{b} = \frac{c}{d}\) thì \(ad = bc\).

b) Tính tỉ số phần trăm, chuyển vế để tìm \(x\).

Lời giải

a) \(\frac{4}{5} = \frac{{ - 12}}{{9 - x}}\)

 \(\begin{array}{l}4(9 - x) =  - 60\\9 - x =  - 15\\x = 24\end{array}\)

Vậy \(x = 24\)

b) \(x + 2,5 = 4.25\% \)

\(\begin{array}{l}x + 2,5 = 1\\x = 1 - 2,5\\x =  - 1,5\end{array}\)

Vậy \(x =  - 1,5\).

Câu 3. (3 điểm)

1. Lớp 6A có 40 học sinh, số học sinh giỏi chiếm 20%  số học sinh cả lớp. Số học sinh khá bằng \(\frac{3}{2}\) số học sinh giỏi, còn lại là học sinh trung bình. Tính số học sinh mỗi loại.

2. Kết thúc học kì I năm học 2022-2023, số học sinh giỏi của các lớp 6A, 6B, 6C, 6D của một trường THCS lần lượt là: 18; 20; 22; 16 (học sinh).

a) Lập bảng thống kê số học sinh giỏi của các lớp 6.

b) Vẽ biểu đồ cột biểu diễn bảng thống kê ở câu a.

3. Một chiếc thùng kín đựng một số quả bóng màu đỏ, màu xanh, màu vàng có cùng kích thước. Trong một trò chơi, người chơi lấy ngẫu nhiên một quả bóng, ghi lại màu rồi trả lại bóng vào thùng.

a) Quả bóng lấy ra có thể có màu gì?

b) Bình thực hiện trò chơi 20 lần và được kết quả như bảng sau:

Tính xác suất thực nghiệm của sự kiện quả bóng lấy ra có màu vàng.

Phương pháp

1. Tính số học sinh giỏi = tổng số học sinh.20%.

Số học sinh khá = số học sinh giỏi . \(\frac{3}{2}\).

Số học sinh trung bình = tổng số học sinh – số học sinh giỏi – số học sinh khá.

2. a) Từ dãy số liệu lập bảng thống kê.

b) Vẽ biểu đồ cột tương ứng.

3. a) Xác định các màu của quả bóng trong thùng có.

b) Tính xác suất thực nghiệm = số lần xuất hiện : tổng số lần thực hiện.

Lời giải

1. Lớp 6A có số học sinh giỏi là: 40.\(\frac{{20}}{{100}}\) = 8 (học sinh)

Số học sinh khá của lớp 6A là: 8.\(\frac{3}{2}\)= 12 (học sinh)

Số học sinh trung bình  của lớp 6A là: 40 – 12 - 8 = 20 (học sinh)

2.

a)

b)

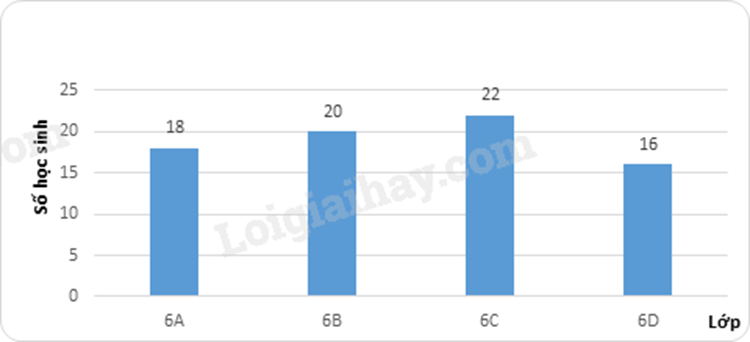
3.

a) Quả bóng lấy ra có thể có màu xanh, màu đỏ hoặc màu vàng.

b) Xác suất thực nghiệm của sự kiện Quả bóng lấy ra có màu vàng là: \(\frac{7}{{20}}\).

Câu 4. (1,5 điểm) Một căn phòng hội trường có nền nhà là hình chữ nhật với chiều dài 14m và chiều rộng 12m. Người ta dự định dùng loại gạch hình vuông có kích thước cạnh 40cm để lát nền đó.

a) Tính diện tích nền nhà hình chữ nhật và diện tích của viên gạch hình vuông.

b) Giả sử một viên gạch để lát sàn là 30 000 đồng, chi phí tiền công lát và các vật liệu khác là 70 000 đồng/m\(^2\). Để lát kín nền nhà bằng loại gạch trên thì người ta phải trả tất cả khoảng bao nhiêu đồng (làm tròn kết quả đến hàng triệu)? Biết rằng các viên gạch được lát liền nhau, coi mạch vữa giữa các viên gạch không đáng kể.

Phương pháp

a) Tính diện tích nền căn phòng = diện tích hình chữ nhật.

Diện tích viên gạch = diện tích hình vuông.

b) Tính tổng số viên gạch = diện tích nền căn phòng : diện tích viên gạch.

Tính tiền gạch, tính tiền công lát nền.

Tổng số tiền = tiền gạch + tiền công.

Làm tròn số đến hàng triệu.

Lời giải

a) Diện tích nền căn phòng hình chữ nhật là: \(12.14 = 168\left( {{m^2}} \right)\) 

Diện tích viên gạch hình vuông là: \(40.40 = 1600\left( {c{m^2}} \right)\) 

b) Đổi 168\({m^2}\) = 1 680 000\(c{m^2}\).

Tổng số viên gạch dùng để lát nền là:

 1 680 000:1 600 = 1 050 (viên)

Tiền gạch để lát nền là: 1 050.30 000 = 31 500 000 (đồng)

Tiền công để lát nền là: 168.70 000 = 11 760 000 (đồng)

Tổng số tiền người ta phải trả để lát nền là:

 31 500 000 + 11 760 000 = 43 260 000 (đồng)

Làm tròn kết quả đến hàng triệu, ta được 43 000 000 đồng.

Vậy người ta phải trả khoảng 43 000 000 đồng.

Câu 5. (2,5 điểm) Cho đoạn thẳng AB = 5cm. Lấy điểm C thuộc đoạn thẳng AB sao cho AC = 1cm.

a) Tính độ dài đoạn thẳng CB.

b) Gọi D là trung điểm của đoạn thẳng CB, tính độ dài đoạn thẳng CD?

c) Vẽ tia Ax là tia đối của tia AB. Lấy điểm E thuộc tia Ax sao cho AE = 3cm. Điểm A có là trung điểm của đoạn thẳng ED? Vì sao?

d) Vẽ tia Ay sao cho \(\widehat {BAy} = 60^\circ \). So sánh góc BAy và góc BAx.

Phương pháp

a) Vì C nằm giữa A và B nên ta tính CB dựa vào AB và AC.

b) Vì D là trung điểm của CB nên ta tính CD theo CB.

c) Điểm A là trung điểm của ED nếu A nằm giữa E, D và AE = AD.

d) Xác định số đo góc BAx rồi so sánh.

Lời giải

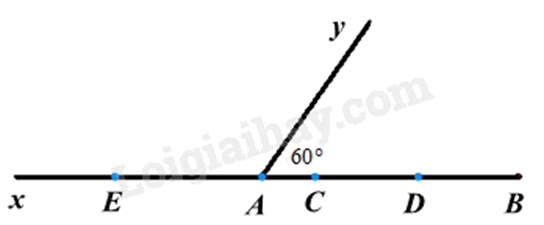
a) Theo hình vẽ, ta có:

\(AC + CB = AB\)

\(1 + CB = 5\)

\(CB = 5 - 1 = 4(cm)\)

b) Vì D là trung điểm của CB nên ta có:

\(CD = \frac{{CB}}{2} = \frac{4}{2} = 2cm\)

c) Theo hình vẽ, ta có: \(AD = AC + CD = 1 + 2 = 3cm\)

Mà \(AE = 3cm\) , suy ra \(AE = AD\)

Mà ta có điểm \(A\) nằm giữa 2 điểm E và D

Vậy suy ra \(A\) là trung điểm của đoạn thẳng \(ED\).

d) Vì \(Ax\) là tia đối của tia \(AB\) nên góc \(BAx\) là góc bẹt

Suy ra \(\widehat {BAx} = 180^\circ \)

\(\widehat {BAy} = 60^\circ \)

Suy ra \(\widehat {BAy} < \widehat {BAx}\).

Câu 6. (0,5 điểm) Cho  M = \(\frac{1}{{{2^3}}}\) + \(\frac{2}{{{3^3}}}\) + \(\frac{3}{{{4^3}}}\)+ .....+ \(\frac{{2021}}{{{{2022}^3}}}\)+ \(\frac{{2022}}{{{{2023}^3}}}\). Chứng tỏ rằng giá trị của M không phải là một số tự nhiên.

Phương pháp

Chứng minh \(\frac{1}{{{k^3}}} < \frac{1}{{{k^2}}} < \frac{1}{{k\left( {k + 1} \right)}} = \frac{1}{k} - \frac{1}{{k + 1}}\) suy ra \(0 < M < 1\) nên M không phải là số tự nhiên.

Lời giải

Ta có: \(\frac{1}{{{2^3}}} < \frac{1}{{{2^2}}} < \frac{1}{{1.2}}\)

           \(\frac{2}{{{3^3}}} < \frac{3}{{{3^3}}} = \frac{1}{{{3^2}}} < \frac{1}{{2.3}}\),

           .......,

           \(\frac{{2022}}{{{{2023}^3}}} < \frac{{2023}}{{{{2023}^3}}} = \frac{1}{{{{2023}^2}}} < \frac{1}{{2022.2023}}\)

nên \(M < \frac{1}{{1.2}} + \frac{1}{{2.3}} + ... + \frac{1}{{2021.2022}} + \frac{1}{{2022.2023}}\)

\( = \frac{1}{1} - \frac{1}{2} + \frac{1}{2} - \frac{1}{3} + ... + \frac{1}{{2021}} - \frac{1}{{2022}} + \frac{1}{{2022}} - \frac{1}{{2023}}\)

\(1 - \frac{1}{{2023}} = \frac{{2022}}{{2023}} < 1\)

Mà M > 0. Vậy 0 < M < 1 nên M không phải là 1 số tự nhiên.