Dạng 3. Phân tích một số ra thừa số nguyên tố Chủ đề 3 Ôn hè Toán 6

Lý thuyết

* Cách 1: Phân tích bằng sơ đồ cây:

Bước 1: Phân tích số n thành tích của hai số bất kì khác 1 và chính nó.

Bước 2: Tiếp tục phân tích ước thứ nhất và ước thứ hai thành tích của hai số bất kì khác 1 và chính nó.

Bước 3: Cứ như vậy đến khi nào xuất hiện số nguyên tố thì dừng lại.

Bước 4: Số n bằng tích của các số cuối cùng của mỗi nhánh.

* Cách 2: Phân tích bằng sơ đồ cột:

Chia số n cho một số nguyên tố (xét từ nhỏ đến lớn), rồi chia thương tìm được cho một số nguyên tố (cũng xét từ nhỏ đến lớn), cứ tiếp tục như vậy cho đến khi thương bằng 1.

Bài tập

Bài 1: Biết \(400 = {2^4}{.5^2}\). Hãy viết 800 thành tích các thừa số nguyên tố

A. \(800 = {2^2}{.5^2}\).

B. \(800 = {2^5}{.5^2}\).

C. \(800 = {2^5}{.5^5}\).

D. \(800 = 400.2\).

Bài 2: Cho cách phân tích 24 thành tích các thừa số nguyên tố như sau.

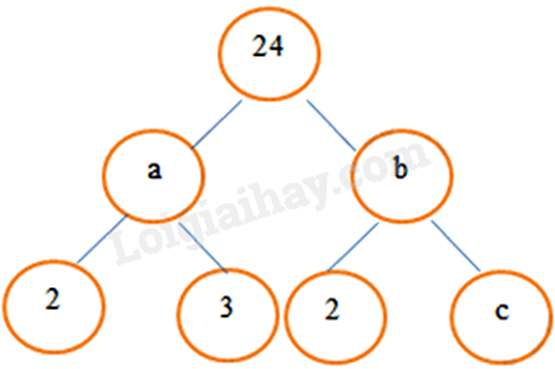
Giá trị của a, b, c lần lượt là:

A. 2, 4, 6.

B. 2, 6, 4.

C. 6, 4, 2.

D. 6, 2, 4.

Bài 3: Số 225 chia hết cho tất cả bao nhiêu số nguyên tố?

A. 9.

B. 3.

C. 5.

D. 2.

Bài 4: Số 40 được phân tích thành các thừa số nguyên tố là:

A. \(40 = 4.10\).

B. \(40 = 2.20\).

C. \(40 = {2^2}.5\).

D. \(40 = {2^3}.5\).

Bài 5: Bạn Hoa đã phân tích số 1092 ra thừa số nguyên tố như sau: 1092 = 3.4.7.13. Theo em, bạn Hoa đã sai ở thừa số nào?

A. 3.

B. 4.

C. 7.

D. 13.

Bài 6: Phân tích các số 315, 150, 213 ra thừa số nguyên tố.

Bài 7: Tìm các số nguyên tố a,b biết:

a) \({a^2}.b.7 = 140\).

b) \({a^3}.b.5 = 120\).

Bài 8: Khi phân tích các số 2150; 1490; 2340 ra thừa số nguyên tố thì số nào có chứa tất cả các thừa số nguyên tố 2; 3 và \(5\)?

Bài 9: Có bao nhiêu số tự nhiên là ước của 312.

Bài 10: Cho phép tính \(\overline {ab} .{\mkern 1mu} c{\mkern 1mu}  = 424.\) Tìm \(\overline {ab} \) và \(c\).

----HẾT----

Lời giải chi tiết:

Bài 1: Biết \(400 = {2^4}{.5^2}\). Hãy viết 800 thành tích các thừa số nguyên tố

A. \(800 = {2^2}{.5^2}\).

B. \(800 = {2^5}{.5^2}\).

C. \(800 = {2^5}{.5^5}\).

D. \(800 = 400.2\).

Phương pháp

- Lấy 800 chia cho 400. Viết 800 thành tích của 400 và thương nhận được.

- Viết 400 thành tích các thừa số nguyên tố.

Lời giải

\(400 = {2^4}{.5^2}\)

\(800 = 400.2 = {2.2^4}{.5^2} = {2^5}{.5^2}\)

Đáp án: B

Bài 2: Cho cách phân tích 24 thành tích các thừa số nguyên tố như sau.

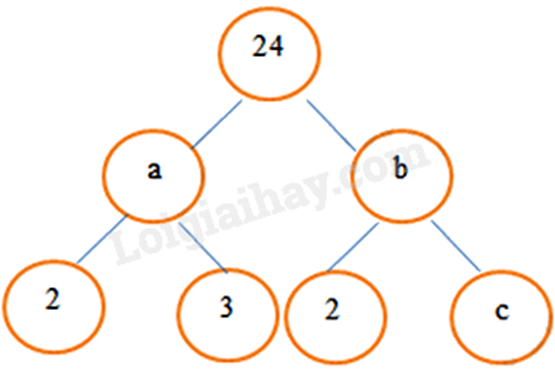
Giá trị của a, b, c lần lượt là:

A. 2, 4, 6.

B. 2, 6, 4.

C. 6, 4, 2.

D. 6, 2, 4.

Phương pháp

Phân tích bằng sơ đồ cây:

Bước 1: Phân tích số n thành tích của hai số bất kì khác 1 và chính nó.

Bước 2: Tiếp tục phân tích ước thứ nhất và ước thứ hai thành tích của hai số bất kì khác 1 và chính nó.

Bước 3: Cứ như vậy đến khi nào xuất hiện số nguyên tố thì dừng lại.

Bước 4: Số n bằng tích của các số cuối cùng của mỗi nhánh.

Lời giải

\(a = 2.3 = 6\)

\(6.b = 24\) nên \(b = 4\)

\(2.c = b\) nên \(c = 4:2 = 2\)

Vậy \(a = 6,b = 4,c = 2\).

Đáp án: C

Bài 3: Số 225 chia hết cho tất cả bao nhiêu số nguyên tố?

A. 9.

B. 3.

C. 5.

D. 2.

Phương pháp

Phân tích các số ra thừa số nguyên tố theo cột dọc hoặc theo sơ đồ cây. Rồi liệt kê các ước nguyên tố của mỗi số.

Lời giải

Số 225 chia hết cho các số nguyên tố: 3; 5

Vậy 225 chia hết cho 2 số nguyên tố.

Đáp án: D

Bài 4: Số 40 được phân tích thành các thừa số nguyên tố là:

A. \(40 = 4.10\).

B. \(40 = 2.20\).

C. \(40 = {2^2}.5\).

D. \(40 = {2^3}.5\).

Phương pháp

Phân tích bằng sơ đồ cây:

Bước 1: Phân tích số n thành tích của hai số bất kì khác 1 và chính nó.

Bước 2: Tiếp tục phân tích ước thứ nhất và ước thứ hai thành tích của hai số bất kì khác 1 và chính nó.

Bước 3: Cứ như vậy đến khi nào xuất hiện số nguyên tố thì dừng lại.

Bước 4: Số n bằng tích của các số cuối cùng của mỗi nhánh.

Lời giải

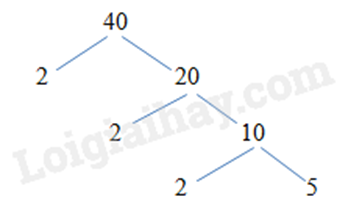
Vậy \(40 = 2.2.2.5 = {2^3}.5\)

Đáp án: D

Bài 5: Bạn Hoa đã phân tích số 1092 ra thừa số nguyên tố như sau: 1092 = 3.4.7.13. Theo em, bạn Hoa đã sai ở thừa số nào?

A. 3.

B. 4.

C. 7.

D. 13.

Phương pháp

Phân tích một số tự nhiên lớn hơn 1 ra thừa số nguyên tố là viết số đó dưới dạng một tích các thừa số nguyên tố.

Lời giải

Vì 1092 = 3.4.7.13 có số 4 không phải là số nguyên tố nên bạn Hoa đã sai ở thừa số 4.

Đáp án: B

Bài 6: Phân tích các số 315, 150, 213 ra thừa số nguyên tố.

Phương pháp

* Cách 1: Phân tích bằng sơ đồ cây:

Bước 1: Phân tích số n thành tích của hai số bất kì khác 1 và chính nó.

Bước 2: Tiếp tục phân tích ước thứ nhất và ước thứ hai thành tích của hai số bất kì khác 1 và chính nó.

Bước 3: Cứ như vậy đến khi nào xuất hiện số nguyên tố thì dừng lại.

Bước 4: Số n bằng tích của các số cuối cùng của mỗi nhánh.

* Cách 2: Phân tích bằng sơ đồ cột:

Chia số n cho một số nguyên tố (xét từ nhỏ đến lớn), rồi chia thương tìm được cho một số nguyên tố (cũng xét từ nhỏ đến lớn), cứ tiếp tục như vậy cho đến khi thương bằng 1.

Lời giải

Vậy

\(\begin{array}{l}315 = {3^2}.5.7;\\150 = {2.3.5^2};\\213 = 3.71.\end{array}\)

Bài 7: Tìm các số nguyên tố a,b biết:

a) \({a^2}.b.7 = 140\).

b) \({a^3}.b.5 = 120\).

Phương pháp

Phân tích 140, 120 thành tích các thừa số nguyên tố.

Lời giải

a) Ta có:

Suy ra \(140 = {2^2}.5.7 = {a^2}.b.7\) nên \(a = 2\), \(b = 5\).

b) Ta có:

Suy ra \(120 = {2^3}.3.5 = {a^3}.b.5\) nên \(a = 2\), \(b = 3\).

Bài 8: Khi phân tích các số 2150; 1490; 2340 ra thừa số nguyên tố thì số nào có chứa tất cả các thừa số nguyên tố 2; 3 và \(5\)?

Phương pháp

Sử dụng cách phân tích một số ra thừa số nguyên tố theo hàng dọc. Từ đó xét xem số nào được phân tích ra thừa số nguyên tố mà chứa cả các thừa số nguyên tố 2; 3 và \(5\).

Lời giải

+) Phân tích số 2150 thành thừa số nguyên tố

Suy ra \(2150 = {2.5^2}.43\)

Vậy số 2150 chỉ chứa thừa số 2, 5.

+) Phân tích số 1490 thành thừa số nguyên tố

Suy ra \(1490 = 2.5.149\)

Vậy số 1490 chỉ chứa thừa số 2, 5.

+) Phân tích số 2340 thành thừa số nguyên tố

Suy ra \(2340 = {2^2}{.3^2}.5.13\)

Vậy số 1490 chứa cả thừa số 2, 3 và 5.

Bài 9: Có bao nhiêu số tự nhiên là ước của 312.

Phương pháp

Bước 1: Phân tích số 312 ra thừa số nguên tố.

Bước 2: Nếu \(a = {p^k}.{q^j}...{r^l}\) thì a có số ước (là số tự nhiên) là: (k+1) . (j + 1) … (l + 1)

Lời giải

Ta được: 312 = 2³ . 3 . 13.

Vậy số ước (là số tự nhiên) của 312 là: (3 + 1) . (1 + 1) . (1 + 1) = 16.

Bài 10: Cho phép tính \(\overline {ab} .{\mkern 1mu} c{\mkern 1mu}  = 424.\) Tìm \(\overline {ab} \) và \(c\).

Phương pháp

Phân tích số 424 ra thừa số nguyên tố, sau đó tìm các ước có hai chữ số và một chữ số của 424.

Từ đó tìm được \(\overline {ab} \) và c.

Lời giải

Vì \(\overline {ab} .{\mkern 1mu} c{\mkern 1mu}  = 424\) nên \(\overline {ab} \) là ước có hai chữ số của 424.

Phân tích số 424 ra thừa số nguyên tố ta được:

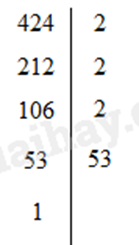
Hay \(424 = {2^3}.53\)

Các ước của 424 là 1; 2; 4; 8; 53; 106; 212; 424

Suy ra \(\overline {ab} {\rm{\;}} = 53\) suy ra \(c = 424:53 = 8.\)

Vậy \(\overline {ab} {\rm{\;}} = 53\), \(c = 424:53 = 8.\)