Đề ôn hè Toán 6 lên 7 - Đề 4

Đề bài

Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:

Câu 1: Tập hợp số nguyên kí hiệu là:

A. \(\mathbb{N}\).

B. \({\mathbb{N}^*}\).

C. \(\mathbb{Q}\).

D. \(\mathbb{Z}\).

Câu 2: Có bao nhiêu số tự nhiên có ba chữ số khác nhau được ghép từ các chữ số 0; 2; 7 chia hết cho 5.

A. 2.

B. 1.

C. 4.

D. 3.

Câu 3: Bạn Hoa đã phân tích số 1092 ra thừa số nguyên tố như sau: 1092 = 3.4.7.13. Theo em, bạn Hoa đã sai ở thừa số nào

A. 3.

B. 4.

C. 7.

D. 13.

Câu 4: Bạn An đã liệt kê ngày sinh của một số bạn trong nhóm để làm bài tập môn Toán và được dãy dữ liệu sau:

10 28 13 35

Em hãy tìm dữ liệu không chính xác.

A. 10.

B. 28.

C. 13.

D. 35.

Câu 5: Điều tra về môn thể thao yêu thích của lớp 6A. Bạn An đã thu thập được các thông tin sau:

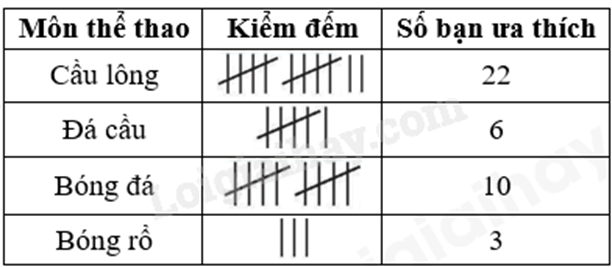
Các môn thể thao được yêu thích của lớp 6A là:

A. Cầu lông, bóng rổ, đá cầu, bóng đá.

B. Cầu lông, bóng rổ, đá cầu, bóng bàn.

C. Bóng rổ, bóng đá, đá cầu.

D. Cầu lông, nhảy dây, bóng đá, đá cầu.

Câu 6: Cho phát biểu sau: “..... là hình có ba cạnh bằng nhau và ba góc bằng nhau”. Điền từ thích hợp vào chỗ trống.

A. Hình vuông.

B. Hình tam giác đều.

C. Hình lục giác đều.

D. Hình chữ nhật.

Câu 7: Trong các cách viết sau đây, cách viết nào không là phân số?

A. \(\frac{{ - 4}}{0}\).

B. \(\frac{{12}}{{ - 19}}\).

C. \(\frac{0}{{12}}\).

D. \(\frac{{ - 3}}{{13}}\).

Câu 8: Tỉ số phần trăm của hai đoạn thẳng \(AB\) và \(CD\) là bao nhiêu, biết rằng \(AB = 3cm\) và \(CD = 5cm\).

A. \(60\% \).

B. \(60\).

C. \(0,6\% \).

D. \(6\).

Câu 9: Cho ba điểm thẳng hàng theo thứ tự \(A,B,C\) biết \(AB = 5cm,\,\,AC = 7cm\). Độ dài đoạn \(BC\) là:

A. \(12cm\).

B. \(6cm\).

C. \(2cm\).

D. \(3cm\).

Câu 10: Trong hình dưới đây, số số góc đỉnh \(A\) là:

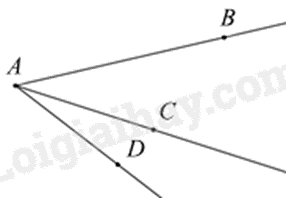
A. 1.

B. 2.

C. 3.

D. 4.

Câu 11: Khả năng mặt sấp xuất hiện khi tung đồng xu là bao nhiêu?

A. 1.

B. 0.

C. \(\frac{1}{2}\).

D. \(\frac{1}{4}\).

Câu 12: Một xạ thủ bắn 30 mũi tên vào một tấm bia thì được 22 lần trúng tâm bia. Xác suất thực nghiệm của sự kiện xạ thủ bắn trúng tấm bia là:

A. \(\frac{{11}}{{26}}\).

B. \(\frac{{26}}{{11}}\).

C. \(\frac{{15}}{{11}}\).

D. \(\frac{{11}}{{15}}\).

Phần tự luận (7 điểm)

Bài 1. (1 điểm) Thực hiện phép tính:

a) \({12^{23}}:{12^{21}} - 2.\left[ {43 - \left( {35:7 - {2^2}} \right) - 20} \right]\)

b) \(\left[ {\left( { - 50,17} \right).20\%  + \left( { - 9,83} \right).20\% } \right]:\left( {3\frac{1}{5}:16} \right)\)

Bài 2. (1 điểm) Tìm \(x\), biết:

a) \(x + \left( { - 21} \right) =  - 35\)

b) \(\left( {\frac{{ - 2}}{3} - x} \right).\frac{3}{2} = 1\frac{2}{5}\)

Bài 3. (2 điểm)

a) Khi sắp xếp lại toàn bộ số quyển sách vừa nhập về của cửa hàng thành từng bó 20 quyển, 24 quyển, 14 quyển thì đều vừa đủ không dư quyển nào. Tính số sách mà cửa hàng vừa nhập về ? biết rằng số quyển sách đó trong khoảng từ 800 đến 900 quyển.

b) Một trường trung học ở Hà Nội tổ chức cuộc thi bình chọn “Cầu thủ được yêu thích nhất” bao gồm Tiến Dũng, Xuân Trường, Văn Đức, Quang Hải. Sau khi bình chọn, thu được kết quả như sau: có \(\frac{1}{7}\) số học sinh chọn Quang Hải, \(\frac{1}{3}\) số học sinh chọn Tiến Dũng, \(50\% \) số học sinh chọn Xuân Trường, còn lại chọn Văn Đức. Biết rằng tổng số học sinh chọn Quang Hải và Tiến Dũng là 400 học sinh. Tính số học sinh chọn Văn Đức.

Bài 4. (2 điểm)

1. Trên tia \(Ox\), lấy hai điểm \(M\) và \(N\) sao cho \(OM = 3cm\), \(ON = 6cm\).

a) Điểm \(M\) có phải là trung điểm của \(ON\) không? Vì sao?

b) Lấy \(K\) là trung điểm của \(OM\). Tính độ dài \(MK\).

2. Góc tạo bởi kim phút và kim giờ tại thời điểm \(3\)giờ, \(6\)giờ, \(8\)giờ và \(11\) giờ lần lượt là bao nhiêu độ?

Bài 5. (1 điểm) Kiểm tra thị lực của hai khối 6 và 8 của một trường THCS, ta thu được kết quả như bảng sau:

a) Tính xác suất thực nghiệm của sự kiện “Học sinh bị tật khúc xạ” của khối lớp 6 và khối lớp 8.

b) Hãy so sánh xem học sinh khối lớp nào bị tật khúc xạ nhiều hơn.

-------- Hết --------

Lời giải

Phần trắc nghiệm

Câu 1: Tập hợp số nguyên kí hiệu là:

A. \(\mathbb{N}\).

B. \({\mathbb{N}^*}\).

C. \(\mathbb{Q}\).

D. \(\mathbb{Z}\).

Phương pháp

Dựa vào kiến thức về tập hợp.

Lời giải

Tập hợp số nguyên kí hiệu là \(\mathbb{Z}\).

Đáp án: D.

Câu 2: Có bao nhiêu số tự nhiên có ba chữ số khác nhau được ghép từ các chữ số 0; 2; 7 chia hết cho 5.

A. 2.

B. 1.

C. 4.

D. 3.

Phương pháp

Các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5.

Từ các chữ số 0; 2; 7 lập các số thoả mãn.

Lời giải

Các số có ba chữ số khác nhau được ghép từ các chữ số 0; 2; 7 là: 270; 207; 720; 702.

Vì các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5 nên chữ số hàng đơn vị là 0 nên các số thoả mãn là 270; 720.

Vậy có 2 số thoả mãn.

Đáp án: A.

Câu 3: Bạn Hoa đã phân tích số 1092 ra thừa số nguyên tố như sau: 1092 = 3.4.7.13. Theo em, bạn Hoa đã sai ở thừa số nào

A. 3.

B. 4.

C. 7.

D. 13.

Phương pháp

Phân tích một số tự nhiên lớn hơn 1 ra thừa số nguyên tố là viết số đó dưới dạng một tích các thừa số nguyên tố.

Lời giải

Vì 1092 = 3.4.7.13 có số 4 không phải là số nguyên tố nên bạn Hoa đã sai ở thừa số 4.

Đáp án: B.

Câu 4: Bạn An đã liệt kê ngày sinh của một số bạn trong nhóm để làm bài tập môn Toán và được dãy dữ liệu sau:

10 28 13 35

Em hãy tìm dữ liệu không chính xác.

A. 10.

B. 28.

C. 13.

D. 35.

Phương pháp

Dựa vào kiến thức về ngày/tháng/năm.

Lời giải

Vì chỉ có tối đa 31 ngày nên ngày sinh là ngày 35 là dữ liệu không chính xác.

Đáp án: D.

Câu 5: Điều tra về môn thể thao yêu thích của lớp 6A. Bạn An đã thu thập được các thông tin sau:

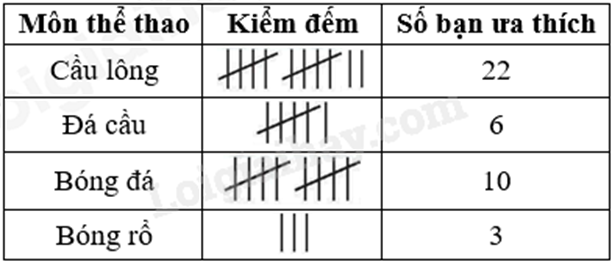
Các môn thể thao được yêu thích của lớp 6A là:

A. Cầu lông, bóng rổ, đá cầu, bóng đá.

B. Cầu lông, bóng rổ, đá cầu, bóng bàn.

C. Bóng rổ, bóng đá, đá cầu.

D. Cầu lông, nhảy dây, bóng đá, đá cầu.

Phương pháp

Dựa vào bảng, xác định các môn thể thao được thu thập.

Lời giải

Các môn thể thao được yêu thích của lớp 6A là: Cầu lông, đá cầu, bóng đá, bóng rổ nên ta chọn đáp án A.

Đáp án: A.

Câu 6: Cho phát biểu sau: “..... là hình có ba cạnh bằng nhau và ba góc bằng nhau”. Điền từ thích hợp vào chỗ trống.

A. Hình vuông.

B. Hình tam giác đều.

C. Hình lục giác đều.

D. Hình chữ nhật.

Phương pháp

Dựa vào khái niệm các hình.

Lời giải

Hình tam giác đều là hình có ba cạnh bằng nhau và ba góc bằng nhau.

Đáp án: B.

Câu 7: Trong các cách viết sau đây, cách viết nào không là phân số?

A. \(\frac{{ - 4}}{0}\).

B. \(\frac{{12}}{{ - 19}}\).

C. \(\frac{0}{{12}}\).

D. \(\frac{{ - 3}}{{13}}\).

Phương pháp

Phân số có dạng \(\frac{a}{b}\), \(\left( {a,b \in \mathbb{Z},b \ne 0} \right)\).

Lời giải

Vì \(\frac{{ - 4}}{0}\) có mẫu số \(b = 0\) (không thoả mãn) nên \(\frac{{ - 4}}{0}\) không phải là phân số.

Đáp án: A.

Câu 8: Tỉ số phần trăm của hai đoạn thẳng \(AB\) và \(CD\) là bao nhiêu, biết rằng \(AB = 3cm\) và \(CD = 5cm\).

A. \(60\% \).

B. \(60\).

C. \(0,6\% \).

D. \(6\).

Phương pháp

Tỉ số phần trăm của hai số a và b là \(\frac{{a.100}}{b}\% \).

Lời giải

Tỉ số phần trăm của hai đoạn thẳng AB và CD là: \(\frac{{3.100}}{5}\%  = 60\% \)

Đáp án: A.

Câu 9: Cho ba điểm thẳng hàng theo thứ tự \(A,B,C\) biết \(AB = 5cm,\,\,AC = 7cm\). Độ dài đoạn \(BC\) là:

A. \(12cm\).

B. \(6cm\).

C. \(2cm\).

D. \(3cm\).

Phương pháp

Chứng minh B nằm giữa A và C.

Tính BC theo AC và AB.

Lời giải

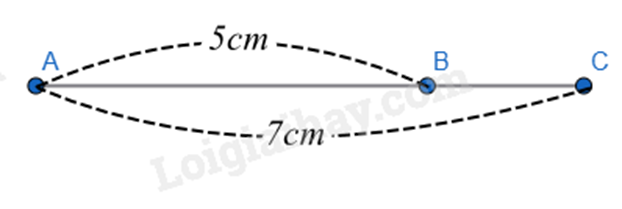
Vì A, B, C thẳng hàng theo thứ tự nên B nằm giữa A và C.

Do đó \(AB + BC = AC\), suy ra \(BC = AC - AB = 7 - 5 = 2\left( {cm} \right)\)

Đáp án: C.

Câu 10: Trong hình dưới đây, số số góc đỉnh \(A\) là:

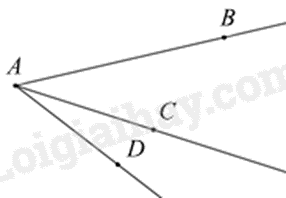
A. 1.

B. 2.

C. 3.

D. 4.

Phương pháp

Liệt kê các góc đỉnh A.

Lời giải

Các góc đỉnh A là: \(\widehat {BAC},\widehat {BAD},\widehat {CAD}\).

Vậy có 3 góc đỉnh A.

Đáp án: C.

Câu 11: Khả năng mặt sấp xuất hiện khi tung đồng xu là bao nhiêu?

A. 1.

B. 0.

C. \(\frac{1}{2}\).

D. \(\frac{1}{4}\).

Phương pháp

Xác định các kết quả khi tung đồng xu.

Lời giải

Khi tung đồng xu ta có thể nhận được mặt sấp hoặc mặt ngửa

Do đó xác suất mặt sấp xuất hiện khi tung đồng xu là: \(\frac{1}{2}\).

Đáp án: C.

Câu 12: Một xạ thủ bắn 30 mũi tên vào một tấm bia thì được 22 lần trúng tâm bia. Xác suất thực nghiệm của sự kiện xạ thủ bắn trúng tấm bia là:

A. \(\frac{{11}}{{26}}\).

B. \(\frac{{26}}{{11}}\).

C. \(\frac{{15}}{{11}}\).

D. \(\frac{{11}}{{15}}\).

Phương pháp

Cách tính xác suất thực nghiệm:

Bước 1: Xác định số lần được kết quả A (kết quả cần tính xác suất) và tổng số lần gieo.

Bước 2: Sử dụng công thức sau để tính xác suất: \(\frac{{n\left( A \right)}}{A}\) = Số lần sự kiện A xảy ra : Tổng số lần thực hiện hoạt động.

Lời giải

Xác suất thực nghiệm của sự kiện xạ thủ bắn trúng tấm bia là: \(\frac{{22}}{{30}} = \frac{{11}}{{15}}\).

Đáp án: D.

Phần tự luận.

Bài 1. (1 điểm) Thực hiện phép tính:

a) \({12^{23}}:{12^{21}} - 2.\left[ {43 - \left( {35:7 - {2^2}} \right) - 20} \right]\)

b) \(\left[ {\left( { - 50,17} \right).20\%  + \left( { - 9,83} \right).20\% } \right]:\left( {3\frac{1}{5}:16} \right)\)

Phương pháp

Thực hiện phép tính theo đúng thứ tự.

Lời giải

a) \({12^{23}}:{12^{21}} - 2.\left[ {43 - \left( {35:7 - {2^2}} \right) - 20} \right]\)

= \({12^2} - 2.\left[ {43 - \left( {5 - 4} \right) - 20} \right]\)

= \(144 - 2.\left[ {43 - 1 - 20} \right]\)

= \(144 - 2.\left[ {42 - 20} \right]\)

= \(144 - 2.22\)

=  144 – 44

= 100

b) \(\left[ {\left( { - 50,17} \right).20\%  + \left( { - 9,83} \right).20\% } \right]:\left( {3\frac{1}{5}:16} \right)\)

\( = \left[ {\left( { - 50,17} \right).\frac{1}{5} + \left( { - 9,83} \right).\frac{1}{5}} \right]:\left( {\frac{{16}}{5}:16} \right)\)

\( = \frac{1}{5}.\left[ {\left( { - 50,17} \right) + \left( { - 9,83} \right){\mkern 1mu} } \right]:\frac{1}{5}\)

\( = \frac{1}{5}.\left( { - 60} \right):\frac{1}{5}\)

\( =  - 60\)

Bài 2. (1 điểm) Tìm \(x\), biết:

a) \(x + \left( { - 21} \right) =  - 35\)

b) \(\left( {\frac{{ - 2}}{3} - x} \right).\frac{3}{2} = 1\frac{2}{5}\)

Phương pháp

Sử dụng quy tắc chuyển vế để tìm x.

a) a + b = c thì a = c – b.

b) Đưa hỗn số về phân số.

a . b = c thì a = c : b

a – b = c thì b = a – c.

Lời giải

a) \(x + \left( { - 21} \right) =  - 35\)

\(\begin{array}{*{20}{l}}{x = --35 - \left( { - 21} \right)}\\{x =  - 14}\end{array}\)

Vậy \(x =  - 14\)

b) \(\left( {\frac{{ - 2}}{3} - x} \right)\;.\;\frac{3}{2} = 1\frac{2}{5}\)

\(\left( {\frac{{ - 2}}{3} - x} \right)\;.\;\frac{3}{2} = \frac{7}{5}\)

\(\left( {\frac{{ - 2}}{3} - x} \right) = \frac{7}{5}:\frac{3}{2}\)

\(\frac{{ - 2}}{3} - x = \frac{{14}}{{15}}\)

\(x = \frac{{ - 2}}{3} - \frac{{14}}{{15}}\)

\(x = \frac{{ - 10}}{{15}} - \frac{{14}}{{15}}\)

\(x =  - \frac{8}{5}\)

Vậy \(x =  - \frac{8}{5}\)

Bài 3. (2 điểm)

a) Khi sắp xếp lại toàn bộ số quyển sách vừa nhập về của cửa hàng thành từng bó 20 quyển, 24 quyển, 14 quyển thì đều vừa đủ không dư quyển nào. Tính số sách mà cửa hàng vừa nhập về ? biết rằng số quyển sách đó trong khoảng từ 800 đến 900 quyển.

b) Một trường trung học ở Hà Nội tổ chức cuộc thi bình chọn “Cầu thủ được yêu thích nhất” bao gồm Tiến Dũng, Xuân Trường, Văn Đức, Quang Hải. Sau khi bình chọn, thu được kết quả như sau: có \(\frac{1}{7}\) số học sinh chọn Quang Hải, \(\frac{1}{3}\) số học sinh chọn Tiến Dũng, \(50\% \) số học sinh chọn Xuân Trường, còn lại chọn Văn Đức. Biết rằng tổng số học sinh chọn Quang Hải và Tiến Dũng là 400 học sinh. Tính số học sinh chọn Văn Đức.

Phương pháp

a) Đưa bài toán về bài toán tìm bội chung.

Phân tích các số ra thừa số nguyên tố.

Tìm BCNN của các số đó.

Tìm BC của các số dựa vào BCNN, kết hợp điều kiện để tìm được kết quả.

b) Xác định phân số ứng với số học sinh chọn Quang Hải và Tiến Dũng.

Tính số học sinh tham gia bình chọn theo công thức tìm một số khi biết giá trị phân số của nó.

Xác định phân số ứng với số học sinh chọn Văn Đức.

Tính số học sinh chọn Văn Đức theo công thức tính giá trị phân số của một số.

Lời giải

a) Vì số quyển sách nhập về khi xếp thành từng bó 24 quyển, 20 quyển, 14 quyển đều vừa đủ nên số quyển sách nhập về là bội chung của 24; 20; 14.

Ta có: \(24 = {2^3}.3\)

           \(\begin{array}{l}20 = {2^2}.5\\14 = 2.7\end{array}\)

Suy ra BCNN(24, 20, 14)  = \({2^3}.3.5.7\) = 840

Do đó BC(24, 20, 14) = {0; 840; 1680; ....}

Do số quyển sách nhập về nằm trong khoảng từ 800 đến 900 quyển nên số quyển sách nhập về là 840 quyển.

Vậy số quyển sách nhập về là 840 quyển

b) Tổng số phần học sinh chọn Quang Hải và Tiến Dũng là:

\(\frac{1}{7} + \frac{1}{3} = \frac{{10}}{{21}}\) (số học sinh)

Số học sinh tham gia bình chọn là:

\(400:\frac{{10}}{{21}} = 400.\frac{{21}}{{10}} = 840\) (học sinh)

Số phần học sinh chọn Văn Đức là:

\(1 - \frac{1}{7} - \frac{1}{3} - 50\%  = 1 - \frac{1}{7} - \frac{1}{3} - \frac{1}{2} = \frac{1}{{42}}\) (số học sinh)

Số học sinh chọn Văn Đức là:

\(840.\frac{1}{{42}} = 20\) (học sinh)

Vậy có 20 học sinh chọn Văn Đức.

Bài 4. (2 điểm)

1. Trên tia \(Ox\), lấy hai điểm \(M\) và \(N\) sao cho \(OM = 3cm\), \(ON = 6cm\).

a) Điểm \(M\) có phải là trung điểm của \(ON\) không? Vì sao?

b) Lấy \(K\) là trung điểm của \(OM\). Tính độ dài \(MK\).

2. Góc tạo bởi kim phút và kim giờ tại thời điểm \(3\)giờ, \(6\)giờ, \(8\)giờ và \(11\) giờ lần lượt là bao nhiêu độ?

Phương pháp

1.

a) Để kiểm tra xem M có phải là trung điểm không, ta kiểm tra:

+ M có nằm giữa O và N không.

+ OM và MN có bằng nhau không.

b) Độ dài MK = OM : 2

2. Vẽ góc tạo bởi kim phút và kim giờ tại các thời điểm rồi đo góc.

Lời giải

1.

a) Trên tia \(Ox\),vì \(OM < ON\) (do \(3cm < 6cm\)) nên \(M\) nằm giữa \(O\) và \(N\).

Suy ra: \(OM + MN = ON\) hay \(3 + MN = 6\), suy ra \(MN = 3cm\)

Vì \(M\) nằm giữa \(O\) và \(N\) và \(OM = MN\left( { = 3cm} \right)\) nên \(M\) là trung điểm \(ON\).

b) Vì \(K\) là trung điểm \(OM\) nên \(MK = OM:2 = 3:2 = 1,5\left( {cm} \right)\).

Vậy \(MK = 1,5cm\).

b)

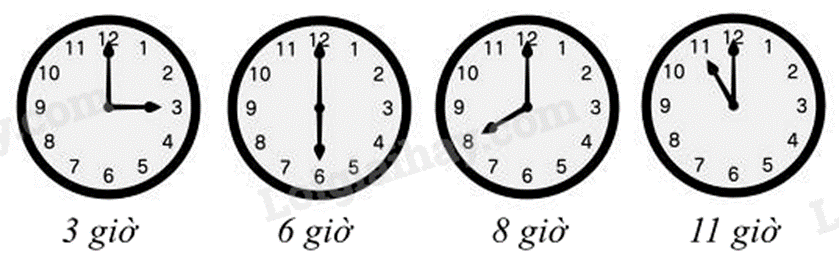
Góc tạo bởi kim phút và kim giờ tại thời điểm 3 giờ, 6 giờ, 8 giờ và 11 giờ lần lượt là \(90^\circ \), \(180^\circ \), \(120^\circ \), \(30^\circ \).

Bài 5. (1 điểm) Kiểm tra thị lực của hai khối 6 và 8 của một trường THCS, ta thu được kết quả như bảng sau:

a) Tính xác suất thực nghiệm của sự kiện “Học sinh bị tật khúc xạ” của khối lớp 6 và khối lớp 8.

b) Hãy so sánh xem học sinh khối lớp nào bị tật khúc xạ nhiều hơn.

Phương pháp

a) Cách tính xác suất thực nghiệm:

Bước 1: Xác định số lần được kết quả A (kết quả cần tính xác suất) và tổng số lần gieo.

Bước 2: Sử dụng công thức sau để tính xác suất: \(\frac{{n\left( A \right)}}{A}\) = Số lần sự kiện A xảy ra : Tổng số lần thực hiện hoạt động.

b) So sánh xác suất thực nghiệm của hai lớp với nhau.

Lời giải

a) Xác suất thực nghiệm của sự kiện “Học sinh bị tật khúc xạ” của khối lớp 6 là: \(50:450 = \frac{1}{9}\).

Xác suất thực nghiệm của sự kiện “ Học sinh bị tật khúc xạ” của khối lớp 8 là: \(35:315 = \frac{1}{7}\).

b) Ta có: \(\frac{1}{9} < \frac{1}{7}\) nên học sinh bị tật khúc xạ của khối lớp 8 nhiều hơn khối lớp 6.