Toán 11 Nâng cao

ÔN TẬP CUỐI NĂM HÌNH HỌC - TOÁN 11 NÂNG CAO

Câu 3 trang 125 SGK Hình học 11 Nâng cao

Cho tam giác ABC và hai hình vuông ABMN, ACPQ như hình 134.

Đề bài

Cho tam giác ABC và hai hình vuông ABMN, ACPQ như hình 134.

a. Xác định phép quay biến tam giác ABQ thành tam giác ANC.

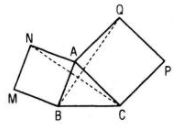
b. Chứng tỏ rằng hai đoạn thẳng BQ, CN bằng nhau và vuông góc với nhau.

c. Gọi O, O’ là tâm của các hình vuông, I là trung điểm của BC. Chứng minh rằng tam giác OIO’ là tam giác vuông cân.

Lời giải chi tiết

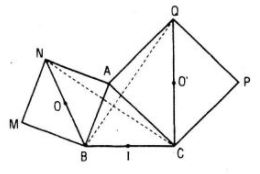
a. Ta có: AB = AN, AQ = AC và góc (AB, AN) bằng góc (AQ, AC) = -90˚

Vậy phép quay tâm A, góc quay φ = -90˚ biến tam giác ABQ thành tam giác ANC.

b. Vì đoạn thẳng BQ biến thành đoạn thẳng NC nên BQ = NC và BQ ⊥ NC.

c. Theo kí hiệu hình bên thì OI // NC, \(OI = {1 \over 2}NC;O'I//QB,O'I = {1 \over 2}BQ\)

vậy từ câu b ta suy ra tam giác IOO’ vuông cân tại đỉnh I.

Loigiaihay.com

Bình luận

Bình chọn:

4.9 trên 7 phiếu

Các bài liên quan: - ÔN TẬP CUỐI NĂM HÌNH HỌC - TOÁN 11 NÂNG CAO

Báo lỗi - Góp ý

>>Học trực tuyến Lớp 11 trên Tuyensinh247.com, mọi lúc, mọi nơi tất cả các môn. Các thầy cô giỏi nổi tiếng, dạy hay dễ hiểu

Các bài khác cùng chuyên mục