Bài 1. Tọa độ của vecto Toán 10 Cánh diều

Lý thuyết Tọa độ của vecto - SGK Toán 10 Cánh diều

A. Lý thuyết 1. Tọa độ của một điểm

Tổng hợp đề thi học kì 1 lớp 10 tất cả các môn - Cánh diều

Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa...

A. Lý thuyết

1. Tọa độ của một điểm

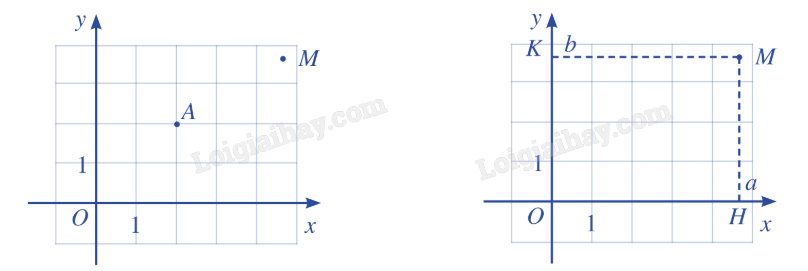
Để xác định tọa độ của một điểm M tùy ý trong mặt phẳng tọa độ Oxy, ta làm như sau:

+ Từ M kẻ đường thẳng vuông góc với trục hoành và cắt trục hoành tại điểm H ứng với số a. Số a là hoành độ của điểm M.

+ Từ M kẻ đường thẳng vuông góc với trục tung và cắt trục tung tại điểm K ứng với số b. Số b là tung độ của điểm M.

Cặp số (a;b) là tọa độ của điểm M trong mặt phẳng tọa độ Oxy. Ta ký hiệu là M(a;b).

2. Tọa độ của một vecto

Tọa độ của điểm M được gọi là tọa độ của vecto \(\overrightarrow {OM} \).

\(\overrightarrow {OM} = (a;b)\) thì a là hoành độ, b là tung độ của \(\overrightarrow {OM} \).

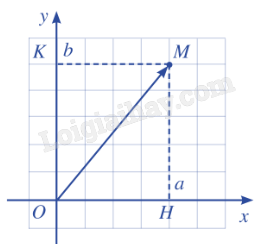
Chú ý: Trong mặt phẳng tọa độ Oxy, ta có:

+ \(\overrightarrow {OM} = (a;b) \Leftrightarrow M(a;b)\).

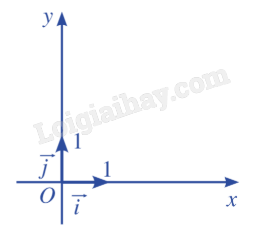
+ Vecto \(\overrightarrow i (1;0)\), \(\overrightarrow j (0;1)\) có điểm gốc O lần lượt là các vecto đơn vị trên trục Ox, Oy.

Với mỗi vecto \(\overrightarrow u \) trong mặt phẳng tọa độ Oxy, tọa độ của vecto \(\overrightarrow u \) là tọa độ của điểm A, trong đó A là điểm sao cho \(\overrightarrow {OA} = \overrightarrow u \).

Ta có định lí sau:

Trong mặt phẳng tọa độ Oxy, nếu \(\overrightarrow u = (a;b)\) thì \(\overrightarrow u = a\overrightarrow i + b\overrightarrow j \).

Ngược lại, nếu \(\overrightarrow u = a\overrightarrow i + b\overrightarrow j \) thì \(\overrightarrow u = (a;b)\).

Chú ý: Với \(\overrightarrow a = ({x_1};{y_1})\) và \(\overrightarrow b = ({x_2};{y_2})\), ta có: \(\overrightarrow a = \overrightarrow b \Leftrightarrow \left\{ \begin{array}{l}{x_1} = {x_2}\\{y_1} = {y_2}\end{array} \right.\).

Như vậy, mỗi vecto hoàn toàn được xác định khi biết tọa độ của nó.

3. Liên hệ giữa tọa độ của điểm và tọa độ của vecto

Trong mặt phẳng tọa độ Oxy, cho hai điểm \(A({x_A};{y_A})\) và \(B({x_B};{y_B})\).

Ta có: \(\overrightarrow {AB} = ({x_B} - {x_A};{y_B} - {y_A})\).

B. Bài tập

Bài 1: Trong mặt phẳng tọa độ Oxy, cho các điểm M, N, P, Q. Tìm tọa độ các vecto \(\overrightarrow {OM} \), \(\overrightarrow {ON} \), \(\overrightarrow {OP} \), \(\overrightarrow {OQ} \).

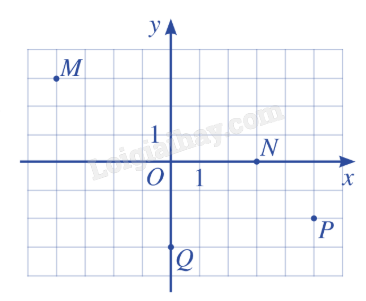
Giải:

Từ hình vẽ, ta có: M(-4;3), N(3;0), P(5;-2), Q(0;-3).

Do đó: \(\overrightarrow {OM} = ( - 4;3)\), \(\overrightarrow {ON} = (3;0)\), \(\overrightarrow {OP} = (5; - 2)\), \(\overrightarrow {OQ} = (0; - 3)\).

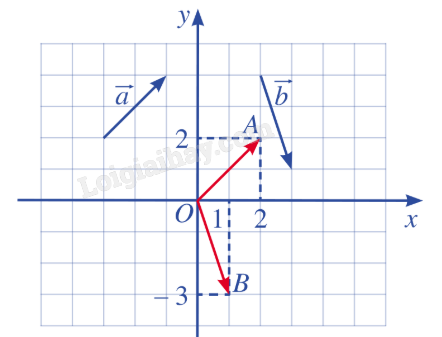
Bài 2: Tìm tọa độ của các vecto \(\overrightarrow a \), \(\overrightarrow b \) trong hình.

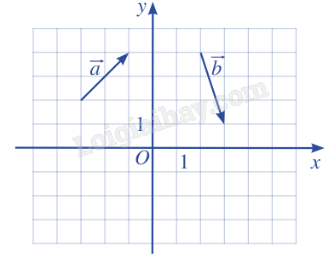
Giải:

Ta có:

\(\overrightarrow a = \overrightarrow {OA} \) và A(2;2); tọa độ vecto \(\overrightarrow {OA} \) chính là tọa độ điểm A nên \(\overrightarrow a = (2;2)\).

\(\overrightarrow b = \overrightarrow {OB} \) và A(1;-3); tọa độ vecto \(\overrightarrow {OB} \) chính là tọa độ điểm B nên \(\overrightarrow b = (1; - 3)\).

Bài 3: Trong mặt phẳng tọa độ Oxy, cho điểm A(1;2) và vecto \(\overrightarrow u = (3; - 4)\).

a) Biểu diễn vecto \(\overrightarrow u \) qua hai vecto \(\overrightarrow i \) và \(\overrightarrow j \).

b) Biểu diễn vecto \(\overrightarrow {OA} \) qua hai vecto \(\overrightarrow i \) và \(\overrightarrow j \).

Giải:

a) Vì \(\overrightarrow u = (3; - 4)\) nên \(\overrightarrow u = 3\overrightarrow i + ( - 4)\overrightarrow j = 3\overrightarrow i - 4\overrightarrow j \).

b) Vì điểm A có tọa độ là (1;2) nên \(\overrightarrow {OA} = (1;2)\). Do đó:

\(\overrightarrow {OA} = 1\overrightarrow i + 2\overrightarrow j = \overrightarrow i + 2\overrightarrow j \).

Bài 4: Trong mặt phẳng tọa độ Oxy, cho ba điểm không thẳng hàng A(1;1), B(4;3), C(-1;-2).

a) Tìm tọa độ của vecto \(\overrightarrow {AB} \).

b) Tìm tọa độ của điểm D sao cho tứ giác ABCD là hình bình hành.

Giải:

a) Ta có: \(\overrightarrow {AB} = (4 - 1;3 - 1)\). Vậy \(\overrightarrow {AB} = (3;2)\).

b) Gọi tọa độ của điểm D là \(({x_D};{y_D})\), ta có: \(\overrightarrow {DC} = ( - 1 - {x_D}; - 2 - {y_D})\).

Tứ giác ABCD là hình bình hành khi và chỉ khi:

\(\overrightarrow {DC} = \overrightarrow {AB} \Leftrightarrow \overrightarrow {DC} = (3;2) \Leftrightarrow \left\{ \begin{array}{l} - 1 - {x_D} = 3\\ - 2 - {y_D} = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_D} = - 4\\{y_D} = - 4\end{array} \right.\).

Vậy D(-4;-4).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải mục I trang 60 SGK Toán 10 tập 2 - Cánh diều
Trong mặt phẳng toạ độ Oxy (Hình 2), hãy: a) Tìm hoành độ và tung độ của điểm A. b) Nêu cách xác định toạ độ của điểm M tuỳ ý.
Giải mục II trang 61, 62, 63 SGK Toán 10 tập 2 - Cánh diều
Cho điểm M trong mặt phẳng toạ độ Oxy. a) Vē vecto OM b) Nêu cách xác định toạ độ của điểm M.
Giải mục III trang 64 SGK Toán 10 tập 2 - Cánh diều
Trong mặt phẳng tọa độ Oxy, cho các điểm: A(1; 3) B(5; -1) C(2; -2) D(-2; 2)
Giải bài 1 trang 65 SGK Toán 10 tập 2 – Cánh diều
Tìm tọa độ của các vecto trong Hình 16 và biểu diễn mỗi vecto đó qua hai vecto
Giải bài 2 trang 65 SGK Toán 10 tập 2 – Cánh diều
Tìm tọa độ của các vecto sau:
Giải bài 3 trang 65 SGK Toán 10 tập 2 – Cánh diều
Tìm các cặp số thực a và b sao cho mỗi cặp vecto sau bằng nhau:
Giải bài 4 trang 66 SGK Toán 10 tập 2 – Cánh diều
Trong mặt phẳng toạ độ Oxy, cho ba điểm A(2;3), B(-1; 1), C(3;- 1).
Giải bài 5 trang 66 SGK Toán 10 tập 2 – Cánh diều
Trong mặt phẳng toạ độ Oxy, cho điểm M(-1; 3). a) Tìm toạ độ điểm A đối xứng với điểm M qua gốc O. b) Tìm toạ độ điểm B đối xứng với điểm M qua trục Ox. c) Tìm toạ độ điểm C đối xứng với điểm M qua trục Oy.
Giải bài 6 trang 66 SGK Toán 10 tập 2 – Cánh diều
Trong mặt phẳng toạ độ Oxy, cho ba điểm không thẳng hàng A(- 3 ; 1), B(-1; 3), I(4;2). Tìm toạ độ của hai điểm C, D sao cho tứ giác ABCD là hình bình hành nhận I làm tâm đối xứng.
Giải bài 7 trang 66 SGK Toán 10 tập 2 – Cánh diều
Trong mặt phẳng toạ độ Oxy, cho tam giác ABC. Các điểm M(1;- 2), N(4;- 1) và P(6 ; 2) lần lượt là trung điểm của các cạnh BC, CA, AB. Tìm toạ độ của các điểm A, B, C.