-
GIẢI SGK TOÁN 11 CÁNH DIỀU - MỚI NHẤT
-
Toán 10 tập 1 - Cánh diều
-
Toán 10 tập 2 - Cánh diều
Giải mục III trang 69, 70 SGK Toán 10 tập 1 - Cánh diều
Cho tam giác ABC nội tiếp đường tròn (O) có bán kính R = 6 và có các góc B = 65, C = 85 Tính độ dài cạnh BC.
Tổng hợp đề thi giữa kì 1 lớp 10 tất cả các môn - Cánh diều
Toán - Văn - Anh - Lí - Hóa - Sinh
Hoạt động 9
Cho $\alpha$ là góc nhọn. Chứng minh:
a) $\widehat{BDC} = \alpha$;
b) $\frac{a}{\sin\alpha} = 2R$.
Lời giải chi tiết:
Xét tam giác $BDC$, ta có $\widehat{BDC} = \alpha$.
Vì $BD$ là đường kính của đường tròn $(O)$ nên $\widehat{BCD} = 90^o$.
Do đó $\sin D = \frac{BC}{BD}$, tức là $\sin\alpha = \frac{a}{2R}$ hay $\frac{a}{\sin\alpha} = 2R$.
Hoạt động 10
Cho $\alpha$ là góc tù. Chứng minh:
a) $\widehat{BDC} = 180^o - \alpha$;
b) $\frac{a}{\sin\alpha} = 2R$.
Lời giải chi tiết:
Xét tam giác $BCD$, ta có: $\widehat{BDC} = 180^o - \alpha$ và $\widehat{BCD} = 90^o$.
Do đó $\sin D = \frac{BC}{BD}$, tức là $\sin(180^o - \alpha) = \frac{a}{2R}$.
Mà $\sin(180^o - \alpha) = \sin\alpha$ nên $\sin\alpha = \frac{a}{2R}$ hay $\frac{a}{\sin\alpha} = 2R$.
Hoạt động 11
Cho \(\alpha \) là góc vuông. Chứng minh \(\frac{a}{{\sin \alpha }} = 2R\).
Phương pháp giải:
Bước 1: Xác định đường tròn ngoài tiếp tam giác, từ đó suy ra bán kính R
Bước 2: Tính \(\frac{a}{{\sin \alpha }}\) rồi so sánh với 2R.
Lời giải chi tiết:
Xét tam giác ABC có \(\widehat A = \alpha = {90^o}\)
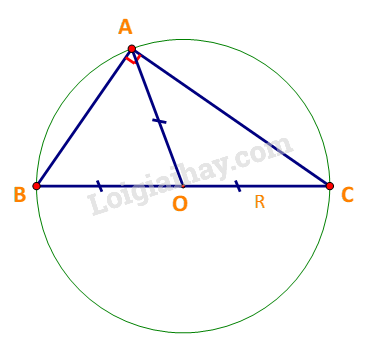
Gọi O là trung điểm của BC. Khi đó: \(OA = OB = OC = \frac{1}{2}BC\)
Do đó đường tròn ngoại tiếp tam giác ABC là (O) bán kính \(R = \frac{{BC}}{2}\)
\( \Rightarrow \frac{a}{{\sin \alpha }} = \frac{{BC}}{{\sin {{90}^o}}} = BC = 2R\) (đpcm)
Luyện tập – vận dụng 3
Cho tam giác ABC nội tiếp đường tròn (O) có bán kính R = 6 và có các góc \(\widehat B = {65^o},\widehat C = {85^o}\). Tính độ dài cạnh BC.
Phương pháp giải:
Bước 1: Tính góc \(\widehat A\).
Bước 2: Áp dụng định lí sin trong tam giác ABC: \(\frac{{BC}}{{\sin A}} = 2R\).
Lời giải chi tiết:
Ta có: \(\widehat B = {65^o},\widehat C = {85^o}\).
\( \Rightarrow \widehat A = {180^o} - \left( {{{65}^o} + {{85}^o}} \right) = {30^o}\).
Áp dụng định lí sin trong tam giác ABC, ta có:
\(\frac{{BC}}{{\sin A}} = 2R \Rightarrow BC = 2R.\sin A\).
Mà \(\widehat A = {30^o},R = 6\).
\( \Rightarrow BC = 2.6.\sin {30^o} = 6\).
Vậy BC = 6.
Bình luận
Chia sẻ
- Giải bài 1 trang 71 SGK Toán 10 tập 1 – Cánh diều
- Giải bài 2 trang 71 SGK Toán 10 tập 1 – Cánh diều
- Giải bài 3 trang 71 SGK Toán 10 tập 1 – Cánh diều
- Giải bài 4 trang 71 SGK Toán 10 tập 1 – Cánh diều
- Giải bài 5 trang 71 SGK Toán 10 tập 1 – Cánh diều
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Cánh diều - Xem ngay
PH/HS Tham Gia Nhóm Lớp 10 Để Trao Đổi Tài Liệu, Học Tập Miễn Phí!
Các bài khác cùng chuyên mục
- Lý thuyết Ba đường conic - SGK Toán 10 Cánh diều
- Lý thuyết Phương trình đường tròn - SGK Toán 10 Cánh diều
- Lý thuyết Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng - SGK Toán 10 Cánh diều
- Lý thuyết Phương trình đường thẳng - SGK Toán 10 Cánh diều
- Lý thuyết Biểu thức tọa độ của các phép toán vecto - SGK Toán 10 Cánh diều
- Lý thuyết Ba đường conic - SGK Toán 10 Cánh diều
- Lý thuyết Phương trình đường tròn - SGK Toán 10 Cánh diều
- Lý thuyết Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng - SGK Toán 10 Cánh diều
- Lý thuyết Phương trình đường thẳng - SGK Toán 10 Cánh diều
- Lý thuyết Biểu thức tọa độ của các phép toán vecto - SGK Toán 10 Cánh diều
