Bài 9. Tích của một vectơ với một số - SBT Toán 10 KNTT

Giải bài 4.13 trang 54 sách bài tập toán 10 - Kết nối tri thức với cuộc sống

Cho tam giác ABC. Gọi D,E tương ứng là trung điểm của BC,CA.

Đề bài

Cho tam giác \(ABC.\) Gọi \(D,\,\,E\) tương ứng là trung điểm của \(BC,\,\,CA.\) Hãy biểu thị các vectơ \(\overrightarrow {AB} ,\,\,\overrightarrow {BC} ,\,\,\overrightarrow {CA} \) theo các vectơ \(\overrightarrow {AD} \) và \(\overrightarrow {BE} .\)

Phương pháp giải - Xem chi tiết

- Tính vectơ \(\overrightarrow {DE} \)

- Tính \(\overrightarrow {AB} \): \(\overrightarrow {AB} = \overrightarrow {AD} + \overrightarrow {DE} + \overrightarrow {EB} \)

- Tính \(\overrightarrow {BC} \): \(\overrightarrow {BC} = 2\overrightarrow {BD} = 2\left( {\overrightarrow {AD} - \overrightarrow {AB} } \right)\)

- Tính \(\overrightarrow {CA} \): \(\overrightarrow {CA} = \overrightarrow {DA} - \overrightarrow {DC} = - \overrightarrow {AD} - \overrightarrow {DC} \)

Lời giải chi tiết

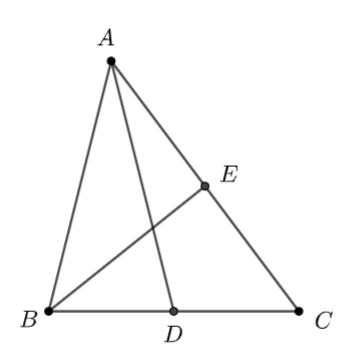
Ta có: \(DE\) là đường trung bình của \(\Delta ABC\)

\( \Rightarrow \) \(\overrightarrow {DE} = - \frac{1}{2}\overrightarrow {AB} \)

Ta có: \(\overrightarrow {AB} = \overrightarrow {AD} + \overrightarrow {DE} + \overrightarrow {EB} = \overrightarrow {AD} - \frac{1}{2}\overrightarrow {AB} + \overrightarrow {EB} \)

\(\begin{array}{l} \Rightarrow \overrightarrow {AB} + \frac{1}{2}\overrightarrow {AB} = \overrightarrow {AD} - \overrightarrow {BE} \\ \Rightarrow \frac{3}{2}\overrightarrow {AB} = \overrightarrow {AD} - \overrightarrow {BE} \\ \Rightarrow \overrightarrow {AB} = \frac{2}{3}\left( {\overrightarrow {AD} - \overrightarrow {BE} } \right) = \frac{2}{3}\overrightarrow {AD} - \frac{2}{3}\overrightarrow {BE} \end{array}\)

Ta có: \(\overrightarrow {BC} = 2\overrightarrow {BD} = 2\left( {\overrightarrow {AD} - \overrightarrow {AB} } \right)\)

\(\begin{array}{l} = 2\left( {\overrightarrow {AD} - \frac{2}{3}\overrightarrow {AD} + \frac{2}{3}\overrightarrow {BE} } \right)\\ = 2\left( {\frac{1}{3}\overrightarrow {AD} + \frac{2}{3}\overrightarrow {BE} } \right) = \frac{2}{3}\overrightarrow {AD} + \frac{4}{3}\overrightarrow {BE} \end{array}\)

Ta có: \(\overrightarrow {CA} = \overrightarrow {DA} - \overrightarrow {DC} = - \overrightarrow {AD} - \overrightarrow {DC} \)

\(\begin{array}{l} = - \overrightarrow {AD} - \frac{1}{2}\left( {\frac{2}{3}\overrightarrow {AD} + \frac{4}{3}\overrightarrow {BE} } \right)\\ = - \overrightarrow {AD} - \frac{1}{3}\overrightarrow {AD} - \frac{2}{3}\overrightarrow {BE} \\ = - \frac{4}{3}\overrightarrow {AD} - \frac{2}{3}\overrightarrow {BE} \end{array}\)