Bài 2. Giải bất phương trình bậc hai một ẩn - SBT Toán ..

Giải bài 2 trang 13 SBT toán 10 - Chân trời sáng tạo

Dựa vào đồ thị của hàm số bậc hai đã cho, hãy nêu tập nghiệm của các bất phương trình bậc hai tương ứng

Tổng hợp đề thi học kì 1 lớp 10 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa...

Đề bài

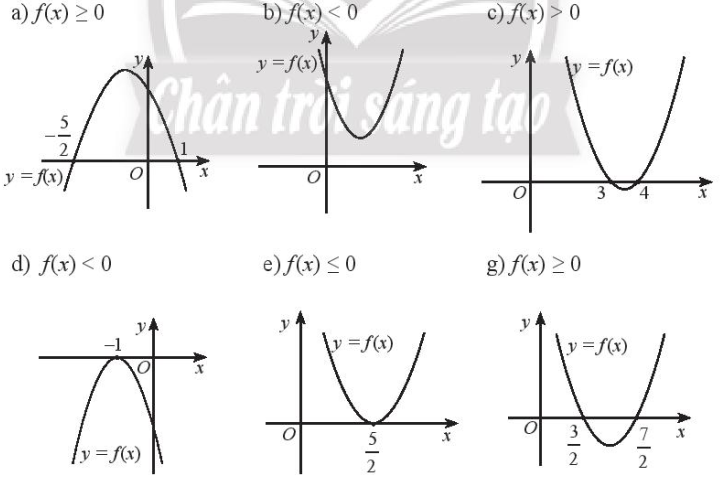
Dựa vào đồ thị của hàm số bậc hai đã cho, hãy nêu tập nghiệm của các bất phương trình bậc hai tương ứng

Lời giải chi tiết

a) Phần đồ thị nằm trên trục hoành tương ứng với \(x \in \left( { - \frac{5}{2};1} \right)\)

Do đó \(f\left( x \right) \ge 0\) khi và chỉ khi \( - \frac{5}{2} \le x \le 1\)

Vậy tập nghiệm của bất phương trình \(f\left( x \right) \ge 0\) là \(\left[ { - \frac{5}{2};1} \right]\)

b) Dễ thấy toàn bộ đồ thị đều nằm phía trên trục hoành, do đó \(f\left( x \right) > 0\) với mọi \(x \in \mathbb{R}\). Vậy tập nghiệm của bất phương trình \(f\left( x \right) < 0\) là \(\emptyset \)

c) Phần đồ thị nằm trên trục hoành tương ứng với \(x \in \mathbb{R}{\rm{\backslash }}\left( {3;4} \right)\)

Do đó\(f\left( x \right) > 0\) khi và chỉ khi \(x < 3\) hoặc \(x > 4\)

Vậy tập nghiệm của bất phương trình \(f\left( x \right) > 0\) là \(\left( { - \infty ;3} \right) \cup \left( {4; + \infty } \right)\)

d) Dễ thấy đồ thị nằm phía dưới trục hoành và cắt trục hoành tại (-1;0)

Do đó \(f\left( x \right) < 0\) khi và chỉ khi \(x \ne - 1\)

Vậy tập nghiệm của bất phương trình \(f\left( x \right) < 0\) là \(\mathbb{R}\backslash \left\{ { - 1} \right\}\)

e) Dễ thấy đồ thị nằm phía trên trục hoành và cắt trục hoành tại \(\left( {\frac{5}{2};0} \right)\)

Do đó \(f\left( x \right) > 0\) với mọi \(x \ne \frac{5}{2}\) và \(f(x) = 0\) tại \(x = \frac{5}{2}\)

Suy ra \(f\left( x \right) \le 0 \Leftrightarrow f(x) = 0 \Leftrightarrow x = \frac{5}{2}\)

Vậy tập nghiệm của bất phương trình \(f\left( x \right) \le 0\) là \(\left\{ {\frac{5}{2}} \right\}\)

g) Phần đồ thị nằm trên trục hoành tương ứng với \(x \in \left( { - \infty ;\frac{3}{2}} \right) \cup \left( {\frac{7}{2}; + \infty } \right)\)

\(f\left( x \right) = 0\) khi và chỉ khi \(x = \frac{3}{2}\) hoặc \(x = \frac{7}{2}\)

Vậy tập nghiệm của bất phương trình \(f\left( x \right) \ge 0\) là \(\left( { - \infty ;\frac{3}{2}} \right] \cup \left[ {\frac{7}{2}; + \infty } \right)\)

Bình luận

Chia sẻ

Bình chọn:

4 trên 3 phiếu

Bài tiếp theo

Giải bài 3 trang 14 SBT toán 10 - Chân trời sáng tạo
Giải các bất phương trình bậc hai sau: a) \( - 9{x^2} + 16x + 4 \le 0\) b) \(6{x^2} - 13x - 33 < 0\)
Giải bài 4 trang 14 SBT toán 10 - Chân trời sáng tạo
Giải các bất phương trình bậc hai sau: a) \({x^2} - 3x < 4\) b) \(0 < 2{x^2} - 11x - 6\)
Giải bài 5 trang 14 SBT toán 10 - Chân trời sáng tạo
Tìm tập xác định của các hàm số sau: a) \(y = \sqrt {15{x^2} + 8x - 12} \) b) \(y = \frac{{x - 1}}{{\sqrt { - 11{x^2} + 30x - 16} }}\) c) \(y = \frac{1}{{x - 2}} - \sqrt { - {x^2} + 5x - 6} \)
Giải bài 6 trang 14 SBT toán 10 - Chân trời sáng tạo
Tìm giá trị của tham số m để: a) \(x = 3\) là một nghiệm của bất phương trình \(\left( {{m^2} - 1} \right){x^2} + 2mx - 15 \le 0\) b) \(x = - 1\) là một nghiệm của bất phương trình \(m{x^2} - 2x + 1 > 0\)
Giải bài 7 trang 14 SBT toán 10 - Chân trời sáng tạo
Với giá trị nào của tham số m thì: a) Phương trình \(4{x^2} + 2\left( {m - 2} \right)x + {m^2} = 0\) có nghiệm b) Phương trình \(\left( {m + 1} \right){x^2} + 2mx - 4 = 0\) có hai nghiệm phân biệt c) Phương trình \(m{x^2} + \left( {m + 1} \right)x + 3m + 10 = 0\) vô nghiệm
Giải bài 8 trang 14 SBT toán 10 - Chân trời sáng tạo
Lợi nhuận thu được từ việc sản xuất và bán x sản phẩm thủ công của một cửa hàng là: \(I\left( x \right) = - 0,1{x^2} + 235x - 70000\) Với I được tính bằng đơn vị nghìn đồng. Với số lượng sản phẩm bán ra là bao nhiêu thì cửa hàng có lãi?
Giải bài 9 trang 15 SBT toán 10 - Chân trời sáng tạo
Một quả bóng được nắm thẳng lên từ độ cao \({h_{_0}}\)(m) với vận tốc \({v_0}\) (m/s). Độ cao của bóng so với mặt đất (tính bằng mét) sau t (s) được cho bởi hàm số
Giải bài 10 trang 15 SBT toán 10 - Chân trời sáng tạo
Từ độ cao \({y_0}\) mét, một quả bóng được ném lên xiên một góc \(\alpha \) so với phương ngang với vạn tốc đầu \({v_0}\) có phương trình chuyển động
Giải bài 11 trang 15 SBT toán 10 - Chân trời sáng tạo
Một hình chữ nhật có chu vi bằng 20 cm. Để tính diện tích hình chữ nhật lớn hơn hoặc bằng 15 cm2 thì chiều rộng của hình chữ nhật nằm trong khoảng bao nhiêu?
Giải bài 12 trang 15 SBT toán 10 - Chân trời sáng tạo
Thiết kế của một chiếc cổng có hình parabol với chiều cao 5 m và khoảng cách giữa hai chân cổng là 4 m.
Giải bài 1 trang 13 SBT toán 10 - Chân trời sáng tạo
\(x = 2\) là một nghiệm của bất phương trình nào sau đây? a) \({x^2} - 3x + 1 > 0\) b) \( - 4{x^2} - 3x + 5 \le 0\) c) \(2{x^2} - 5x + 2 \le 0\)