Toán 10, giải toán lớp 10 chân trời sáng tạo Bài tập cuối chương V Toán 10 Chân trời sáng tạo

Giải bài 12 trang 103 SGK Toán 10 tập 1 – Chân trời sáng tạo


Một chiếc thuyền cố gắng đi thẳng qua một con sông với tốc độ 0,75 m/s. Tuy nhiên dòng chảy của nước trên con sông đó chạy với tốc độ 1,20 m/s về hướng bên phải.

Đề bài

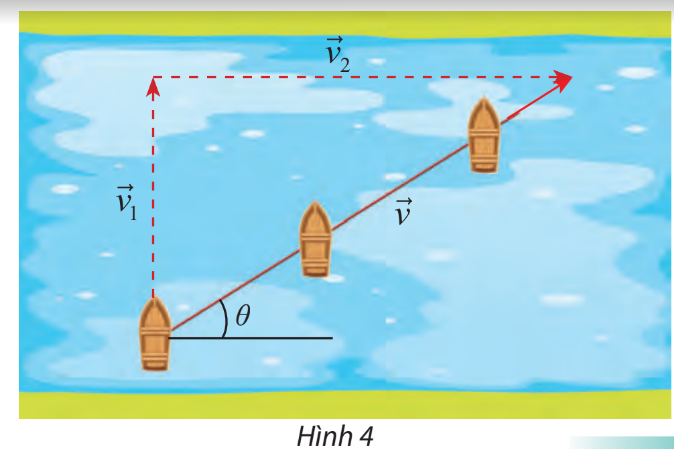
Một chiếc thuyền cố gắng đi thẳng qua một con sông với tốc độ 0,75 m/s. Tuy nhiên dòng chảy của nước trên con sông đó chạy với tốc độ 1,20 m/s về hướng bên phải. Gọi \(\overrightarrow {{v_1}} ,\overrightarrow {{v_2}} ,\overrightarrow v \) lần lượt là vận tốc của thuyền so với dòng nước, vận tốc của dòng nước so với bờ và vận tốc của thuyền so với bờ.

a) Tính độ dài của các vectơ \(\overrightarrow {{v_1}} ,\overrightarrow {{v_2}} ,\overrightarrow v \)

b) Tốc độ dịch chuyển của thuyền so với bờ là bao nhiêu?

c)  Hướng di chuyển của thuyền lệch một góc bao nhiêu so với bờ?

Phương pháp giải - Xem chi tiết

a) Sử dụng tính chất trong tam giác vuông \({c^2} = {a^2} + {b^2}\) (với c là cạnh huyền của tam giác vuông và a, b là cạnh góc vuông)

b) Chỉ ra kết quả độ dài vectơ \(\overrightarrow v \) đã tính được ở câu a)

c) Sử dụng tính chất trong tam giác vuông \(\sin B = \frac{a}{c}\) (với c là cạnh huyền của tam giác vuông và a, b là cạnh góc vuông)

Lời giải chi tiết

a) Ta có:

\(\left| {\overrightarrow {{v_1}} } \right| = 0,75;\left| {\overrightarrow {{v_2}} } \right| = 1,20\)

Dựa vào hình vẽ ta thấy \(\overrightarrow v  = \overrightarrow {{v_1}}  + \overrightarrow {{v_2}} \) và \(\overrightarrow {{v_1}}  \bot \overrightarrow {{v_2}} \)

Áp dụng tính chất trong tam giác vuông ta có: \({\left| {\overrightarrow v } \right|^2} = {\left| {\overrightarrow {{v_1}} } \right|^2} + {\left| {\overrightarrow {{v_2}} } \right|^2} \Rightarrow \left| {\overrightarrow v } \right| = \sqrt {{{\left| {\overrightarrow {{v_1}} } \right|}^2} + {{\left| {\overrightarrow {{v_2}} } \right|}^2}}  = \sqrt {0,{{75}^2} + 1,{2^2}}  = \frac{{3\sqrt {89} }}{{20}}\)

b) Tốc độ dịch chuyển của thuyền so với bờ là \(\frac{{3\sqrt {89} }}{{20}}\) m/s

c) Nước có hướng dichuyển song song với bờ nên hướng di chuyển của thuyền

so với bờ tương đương với hướng di chuyển của thuyền so với nước

Suy ra góc lệch giữa hướng di chuyển của thuyền và bờ là \(\left( {\overrightarrow v ,\overrightarrow {{v_2}} } \right)\)

Ta có: \(\sin \left( {\overrightarrow v ,\overrightarrow {{v_2}} } \right) = \frac{{\left| {\overrightarrow {{v_1}} } \right|}}{{\left| {\overrightarrow v } \right|}} = \frac{{0,75}}{{\frac{{3\sqrt {89} }}{{20}}}} = \frac{{5\sqrt {89} }}{{89}} \Rightarrow \left( {\overrightarrow v ,\overrightarrow {{v_2}} } \right) \simeq 32^\circ \)

Vậy hướng di chuyển của thuyền lệch một góc \(32^\circ \) so với bờ


Bình chọn:
3.6 trên 5 phiếu

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 10 - Chân trời sáng tạo - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store