Đề thi vào lớp 6 môn Toán trường THCS Chu Văn An, THCS Chùa Hang II Thành phố Thái Nguyên năm 2025

Đề bài

I. PHẦN TRẮC NGHIỆM (2,0 điểm - gồm 4 câu; mỗi câu 0,5 điểm)

Chọn 01 phương án trả lời đúng cho mỗi câu sau (Học sinh trả lời vào giấy viết bài đánh giá năng lực, ví dụ: 1A, 2B,...):

Câu 1. 15% của 60 kg là:

A. 0,9 kg                    B. 9 kg                                   C. 90 kg                     D. 4 kg

Câu 2. Phân số $\frac{{18}}{{50}}$ viết thành phân số thập phân là:

A. $\frac{9}{{25}}$                        B. $\frac{{54}}{{150}}$                 C. $\frac{{36}}{{100}}$                 D. $\frac{{72}}{{200}}$

Câu 3. Phân số nào dưới đây là phân số tối giản?

A. $\frac{{11}}{{23}}$                               B. $\frac{{18}}{{21}}$                               C. $\frac{{13}}{{52}}$                        D. $\frac{{34}}{{51}}$

Câu 4. Một bể cá hình hộp chữ nhật có chiều dài 60 cm, chiều rộng 25cm, chiều cao 50 cm. Hỏi bể cá này chứa được tối đa bao nhiêu lít nước?

A. 75 000 $\ell $                   B. 7 500 $\ell $                     C. 75 $\ell $              D. 7,5 $\ell $

II. PHẦN TỰ LUẬN (8,0 điểm)

Bài 1 (1,0 điểm).

a) Tìm x biết: $5\times x+2=52$

b) Tính giá trị biểu thức A = 15,8 – 7,5 : 2,5 × 3,6

Bài 2 (1,0 điểm). Trên bản đồ tỉ lệ 1 : 2 000 000, chiều dài tuyến đường sắt Hà Nội - Thái Nguyên đo được là 4 cm. Hỏi trên thực tế tuyến đường đó dài khoảng bao nhiêu ki-lô-mét?

Bài 3 (1,5 điểm). Lớp 5A có nhiều hơn lớp 5B là 4 học sinh. Số học sinh lớp 5A bằng $\frac{10}{9}$ số học sinh lớp 5B. Hỏi mỗi lớp có bao nhiêu học sinh?

Bài 4 (2,5 điểm). Cho hình chữ nhật ABCD với AB = 14 cm, BC = 6 cm. Nối A với C, trên AC lấy điểm M sao cho AM = $\frac{2}{3}$AC. Kéo dài DM cắt BC tại điểm E.

a) Tính diện tích hình tam giác ADE.

b) Tính độ dài đoạn thẳng CE.

Bài 5 (1,0 điểm). Bạn An tung một đồng xu 30 lần và thu được kết quả như sau: số lần xuất hiện mặt ngửa bằng $\frac{2}{3}$ số lần xuất hiện mặt sấp.

a) Viết tỉ số của số lần xuất hiện mặt ngửa và tổng số lần tung đồng xu.

b) Có bao nhiêu lần xuất hiện mặt sấp? Bao nhiêu lần xuất hiện mặt ngửa?

Bài 6 (1,0 điểm). Trong một hộp có 10 tấm thẻ và trên mỗi tấm thẻ đều ghi một số trong các số 3; 5 hoặc 7. Không nhìn vào hộp, bạn Nam rút ra 6 tấm thẻ bất kỳ. Hãy cho biết tổng các số ghi trên 6 tấm thẻ được rút ra bằng bao nhiêu? Biết rằng, tổng đó là một trong các số 16; 19; 26; 31; 41; 44.

Đáp án

HƯỚNG DẪN GIẢI CHI TIẾT

I. PHẦN TRẮC NGHIỆM (2,0 điểm - gồm 4 câu; mỗi câu 0,5 điểm)

Chọn 01 phương án trả lời đúng cho mỗi câu sau (Học sinh trả lời vào giấy viết bài đánh giá năng lực, ví dụ: 1A, 2B,...):

Câu 1. 15% của 60 kg là:

A. 0,9 kg                    B. 9 kg                                   C. 90 kg                     D. 4 kg

Cách giải:

15% của 60 kg là: 60 : 100 x 15 = 9 (kg)

Đáp án: B

Câu 2. Phân số $\frac{{18}}{{50}}$ viết thành phân số thập phân là:

A. $\frac{9}{{25}}$                        B. $\frac{{54}}{{150}}$                 C. $\frac{{36}}{{100}}$                 D. $\frac{{72}}{{200}}$

Cách giải:

$\frac{{18}}{{50}} = \frac{{18 \times 2}}{{50 \times 2}} = \frac{{36}}{{100}}$

Đáp án: C

Câu 3. Phân số nào dưới đây là phân số tối giản?

A. $\frac{{11}}{{23}}$                               B. $\frac{{18}}{{21}}$                               C. $\frac{{13}}{{52}}$                        D. $\frac{{34}}{{51}}$

Cách giải:

Phân số tối giản trong các phân số đã cho là: $\frac{{11}}{{23}}$

Đáp án: A

Câu 4. Một bể cá hình hộp chữ nhật có chiều dài 60 cm, chiều rộng 25cm, chiều cao 50 cm. Hỏi bể cá này chứa được tối đa bao nhiêu lít nước?

A. 75 000 $\ell $                   B. 7 500 $\ell $                     C. 75 $\ell $              D. 7,5 $\ell $

Cách giải:

Thể tích của bể cá đó là: 60 x 25 x 50 = 75 000 (cm³) = 75 dm³ = 75 lít

Đáp án: C

II. PHẦN TỰ LUẬN (8,0 điểm)

Bài 1 (1,0 điểm).

a) Tìm x biết: $5 \times x + 2 = 52$

b) Tính giá trị biểu thức A = 15,8 – 7,5 : 2,5 × 3,6

Cách giải:

a) $5 \times x + 2 = 52$

$5 \times x = 52 - 2$

$5 \times x = 50$

$x = 50:5$

$x = 10$

b) A = 15,8 – 7,5 : 2,5 × 3,6

    A = 15,8 – 3 x 3,6

    A = 15,8 – 10,8

    A = 5

Bài 2 (1,0 điểm). Trên bản đồ tỉ lệ 1 : 2 000 000, chiều dài tuyến đường sắt Hà Nội - Thái Nguyên đo được là 4 cm. Hỏi trên thực tế tuyến đường đó dài khoảng bao nhiêu ki-lô-mét?

Cách giải:

Trên thực tế tuyến đường đó dài khoảng số ki-lô-mét là:

4 x 2 000 000 = 8 000 000 (cm) = 80 km

Đáp số: 80 km

Bài 3 (1,5 điểm). Lớp 5A có nhiều hơn lớp 5B là 4 học sinh. Số học sinh lớp 5A bằng $\frac{{10}}{9}$ số học sinh lớp 5B. Hỏi mỗi lớp có bao nhiêu học sinh?

Cách giải:

Hiệu số phần bằng nhau là là;

10 – 9 = 1 (phần)

Số học sinh lớp 5A là:

4 : 1 x 10 = 40 (học sinh)

Số học sinh lớp 5B là:

40 – 4 = 36 (học sinh)

Lớp 5A: 40 học sinh

Lớp 5B: 36 học sinh

Bài 4 (2,5 điểm). Cho hình chữ nhật ABCD với AB = 14 cm, BC = 6 cm. Nối A với C, trên AC lấy điểm M sao cho AM = $\frac{2}{3}$AC. Kéo dài DM cắt BC tại điểm E.

a) Tính diện tích hình tam giác ADE.

b) Tính độ dài đoạn thẳng CE.

Cách giải:

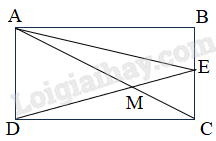
a) Diện tích hình tam giác ADE là 14 x 6 : 2 = 42 (cm²)

b) S_EAM = 2 x S_EMC (Hai tam giác có chung chiều cao hạ từ đỉnh E và đáy AM = 2 MC.

Suy ra chiều cao hạ từ A xuống đáy ME bằng 2 lần chiều cao hạ từ C xuống đáy ME.

Suy ra S_ADE = 2 x S_CDE

Suy ra S_CDE = 42 : 2 = 21(cm²)

Độ dài đoạn thẳng CE là 2 x S_CDE : DC =  21 x 2 : 14 = 3 (cm)

Bài 5 (1,0 điểm). Bạn An tung một đồng xu 30 lần và thu được kết quả như sau: số lần xuất hiện mặt ngửa bằng $\frac{2}{3}$ số lần xuất hiện mặt sấp.

a) Viết tỉ số của số lần xuất hiện mặt ngửa và tổng số lần tung đồng xu.

b) Có bao nhiêu lần xuất hiện mặt sấp? Bao nhiêu lần xuất hiện mặt ngửa?

Cách giải:

a) Tỉ số của số lần xuất hiện mặt ngửa và tổng số lần tung đồng xu là $\frac{2}{5}$

b) Số lần xuất hiện mặt ngửa là $30 \times \frac{2}{3} = 20$ (lần)

    Số lần xuất hiện mặt sấp là: 30 – 20 = 10 (lần)

Bài 6 (1,0 điểm). Trong một hộp có 10 tấm thẻ và trên mỗi tấm thẻ đều ghi một số trong các số 3; 5 hoặc 7. Không nhìn vào hộp, bạn Nam rút ra 6 tấm thẻ bất kỳ. Hãy cho biết tổng các số ghi trên 6 tấm thẻ được rút ra bằng bao nhiêu? Biết rằng, tổng đó là một trong các số 16; 19; 26; 31; 41; 44.

Cách giải:

• Mỗi thẻ là 3, 5 hoặc 7 → đều là số lẻ. Lấy 6 tấm (số chẵn) thì tổng phải là số chẵn.
• Nếu cả 6 thẻ đều là 3 thì tổng là 3+ 3 + 3 + 3 + 3 + 3 = 18
  Từ 18, nếu đổi một thẻ 3 thành 5 thì tổng tăng 2;
  nếu đổi 3 thành 7 thì tổng tăng 4.

Vậy mọi tổng có thể có dạng: 18 cộng thêm vài lần 2 hoặc 4.

So với các số đã cho

• 16: nhỏ hơn 18 (loại)
• 19, 31, 41: số lẻ (loại)
• 44: muốn lên 44 phải tăng 26 từ 18, mà mỗi lần chỉ tăng 2 hoặc 4, tối đa 6 lần (vì có 6 thẻ): tăng nhiều nhất 6 x 4 = 24 → không tới 26, nên không thoả mãn.
• 26: từ 18 lên 26 là tăng 8. Tăng 8 có thể làm được:
• 4 + 4 (đổi 2 thẻ 3 → 7), hoặc
• 2 + 2 + 4 (đổi 2 thẻ 3 → 5 và 1 thẻ 3 → 7)
• 2 + 2 + 2 + 2 (đổi 4 thẻ 3 → 5).
  ⇒ Thoả mãn.

Vậy tổng các số được ghi trên tấm thr rút ra là 26.