 Đề thi vào lớp 6 môn toán có đáp án - 9 năm gần nhất
Đề thi vào lớp 6 môn toán có đáp án - 9 năm gần nhất
 Đề thi vào lớp 6 môn Toán trường Ngôi Sao - Hà Nội
Đề thi vào lớp 6 môn Toán trường Ngôi Sao - Hà Nội Đề thi vào lớp 6 môn Toán trường Ngôi sao năm 2025
Tải vềHiện nay tuổi em gấp bốn lần tuổi em khi tuổi anh bằng tuổi em hiện nay. Hai người dự định cùng làm một công việc trong 5 giờ sẽ xong.
Đề bài
MỘT SỐ BÀI TOÁN TRONG KÌ THI HỌC BỔNG NGÔI SAO HÀ NỘI
Năm học: 2025 – 2026
Môn: Toán lớp 5
Thời gian làm bài: 60 phút
PHẦN I. TRẮC NGHIỆM
Câu 1. Viết số gồm 3 trăm, 6 đơn vị và 2 phần trăm.
Câu 2. Tính diện tích phần tô đậm, biết hình tròn lớn có đường kính là 10 cm, hình tròn bé có đường kính là 7 cm.

Câu 3. Hiện nay tuổi em gấp bốn lần tuổi em khi tuổi anh bằng tuổi em hiện nay. Khi tuổi em bằng tuổi anh hiện nay thì tổng số tuổi hai anh em là 51 tuổi. Tính tuổi mỗi người hiện nay.
Câu 4. Hai người dự định cùng làm một công việc trong 5 giờ sẽ xong. Làm được 2 giờ người thứ nhất có việc bận cần phải đi nên chỉ còn người thứ hai làm. Người thứ hai làm nốt công việc đó trong 9 giờ. Hỏi nếu làm riêng thì mỗi người làm công việc đó trong bao lâu?
Câu 5. Cho $A = \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + .... + \frac{1}{{152}}$
$B = \frac{1}{{1 + 2}} + \frac{1}{{1 + 2 + 3}} + \frac{1}{{1 + 2 + 3 + 4}} + ... + \frac{1}{{1 + 2 + 3 + .... + 511}}$
Tính $\frac{A}{B}$
Câu 6. Cho tam giác ABC. Lấy M và N lần lượt là trung điểm của cạnh AB và AC, nối M với C và N với B cắt nhau tại O. Tính SABC, biết SMOB = 20 cm2.
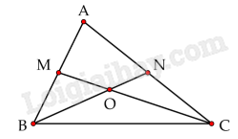
PHẦN 2. TỰ LUẬN
Bài 1. Tìm x biết $x + 3,8 = 3,5 \times 1,5$
Bài 2. Tổng số gạo bán cả 3 ngày là 125,6 tạ gạo. Số gạo bán ngày thứ ba hơn số gạo bán ngày thứ nhất và ngày thứ hai là 19 tạ gạo. Số gạo bán ngày thứ hai bằng 30% số gạo bán ngày thứ nhất. Hỏi mỗi ngày bán được bao nhiêu tạ gạo?
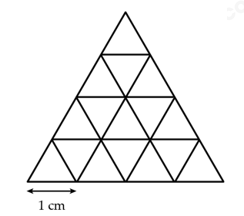
Bài 3. Cho hình vẽ bên.
a) Có bao nhiêu hình tam giác được cấu tạo bởi các hình tam giác có cạnh là 1 cm?
b) Xóa 2 đoạn 1 cm để được ít hình tam giác nhất.
Đáp án
HƯỚNG DẪN GIẢI CHI TIẾT
PHẦN I. TRẮC NGHIỆM
Câu 1. Viết số gồm 3 trăm, 6 đơn vị và 2 phần trăm.
Cách giải:
Số gồm 3 trăm, 6 đơn vị và 2 phần trăm là 306,02.
Câu 2. Tính diện tích phần tô đậm, biết hình tròn lớn có đường kính là 10 cm, hình tròn bé có đường kính là 7 cm.

Cách giải
Bán kính hình tròn lớn là 10 : 2 = 5 (cm)
Diện tích hình tròn lớn là 5 x 5 x 3,14 = 78,5 (cm2)
Bán kính hình tròn bé là 7 : 2 = 3,5 (cm)
Diện tích hình tròn bé là 3,5 x 3,5 x 3,14 = 38,465 (cm2)
Diện tích phần tô đậm là 78,5 - 38,465 = 40,035 (cm2)
Đáp án: 40,035 cm2
Câu 3. Hiện nay tuổi em gấp bốn lần tuổi em khi tuổi anh bằng tuổi em hiện nay. Khi tuổi em bằng tuổi anh hiện nay thì tổng số tuổi hai anh em là 51 tuổi. Tính tuổi mỗi người hiện nay.
Cách giải:
Ta có sơ đồ khi tuổi anh bằng tuổi em hiện nay:
Em: I − −I
Anh: I − −I − −I − −I − −I
Hiệu số tuổi của hai anh em không đổi nên tuổi anh sẽ hơn tuổi em số phần là: 4 – 1 = 3 (phần)
Ta có sơ đồ hiện nay:
Em: I − −I − −I − −I − −I
Anh: I − −I − −I − −I − −I − −I − −I − −I
Ta có sơ đồ khi tuổi em bằng tuổi anh hiện nay:
Em: I − −I − −I − −I − −I − −I − −I − −I
Anh: I − −I − −I − −I − −I − −I − −I − −I − −I − −I − −I
51 tuổi ứng với số phần là: 7 + 10 = 17 (phần)
Giá trị của một phần là: 51 : 17 = 3 (tuổi)
Tuổi em hiện nay là: 3 x 4 = 12 (tuổi)
Tuổi chị hiện nay là: 3 x 7 = 21 (tuổi)
Đáp án: Tuổi anh: 21 tuổi; tuổi em: 12 tuổi
Câu 4. Hai người dự định cùng làm một công việc trong 5 giờ sẽ xong. Làm được 2 giờ người thứ nhất có việc bận cần phải đi nên chỉ còn người thứ hai làm. Người thứ hai làm nốt công việc đó trong 9 giờ. Hỏi nếu làm riêng thì mỗi người làm công việc đó trong bao lâu?
Cách giải:
1 giờ hai người làm được số phần công việc là: $1:5 = \frac{1}{5}$ (công việc)
2 giờ hai người làm được số phần công việc là: $\frac{1}{5} \times 2 = \frac{2}{5}$ (công việc)
Số phần công việc còn lại là: $1 - \frac{2}{5} = \frac{3}{5}$ (công việc)
1 giờ người thứ hai làm được số phần công việc là: $\frac{3}{5}:9 = \frac{1}{{15}}$ (công việc)
Người thứ hai làm một mình thì sau số thời gian hoàn thành công việc là: $1:\frac{1}{{15}} = 15$ (giờ)
1 giờ người thứ nhất làm được số phần công việc là: $\frac{1}{5} - \frac{1}{{15}} = \frac{2}{{15}}$ (công việc)
Người thứ nhất làm một mình thì sau số thời gian hoàn thành công việc là: $1:\frac{2}{{15}} = 7,5$ (giờ)
Đáp án: Người thứ nhất: 7,5 giờ; người thứ hai: 15 giờ
Câu 5. Cho $A = \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + .... + \frac{1}{{152}}$
$B = \frac{1}{{1 + 2}} + \frac{1}{{1 + 2 + 3}} + \frac{1}{{1 + 2 + 3 + 4}} + ... + \frac{1}{{1 + 2 + 3 + .... + 511}}$
Tính $\frac{A}{B}$
Cách giải
$A = \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + .... + \frac{1}{{152}}$
$A \times 2 = 1 + \frac{1}{2} + \frac{1}{4} + .... + \frac{1}{{256}}$
$A \times 2 - A = 1 - \frac{1}{{512}}$
$A = \frac{{511}}{{512}}$
$B = \frac{1}{{1 + 2}} + \frac{1}{{1 + 2 + 3}} + \frac{1}{{1 + 2 + 3 + 4}} + ... + \frac{1}{{1 + 2 + 3 + .... + 511}}$
$B = \frac{1}{{(1 + 2) \times 2:2}} + \frac{1}{{(1 + 3) \times 3:2}} + \frac{1}{{(1 + 4) \times 4:2}} + .... + \frac{1}{{(1 + 511) \times 511:2}}$
$B = \frac{1}{{2 \times 3:2}} + \frac{1}{{3 \times 4:2}} + \frac{1}{{4 \times 5:2}} + .... + \frac{1}{{511 \times 512:2}}$
$B \times \frac{1}{2} = \frac{1}{{2 \times 3}} + \frac{1}{{3 \times 4}} + \frac{1}{{4 \times 5}} + .... + \frac{1}{{511 \times 512}}$
$B \times \frac{1}{2} = \frac{1}{2} - \frac{1}{3} + \frac{1}{3} - \frac{1}{4} + \frac{1}{4} - \frac{1}{5} + .... + \frac{1}{{511}} - \frac{1}{{512}}$
$B \times \frac{1}{2} = \frac{1}{2} - \frac{1}{{512}} = \frac{{255}}{{512}}$
$B = \frac{{255}}{{512}}:\frac{1}{2} = \frac{{510}}{{512}}$
Ta có $\frac{A}{B} = \frac{{511}}{{512}}:\frac{{510}}{{512}} = \frac{{511}}{{510}}$
Đáp án: $\frac{{511}}{{510}}$
Câu 6. Cho tam giác ABC. Lấy M và N lần lượt là trung điểm của cạnh AB và AC, nối M với C và N với B cắt nhau tại O. Tính SABC, biết SMOB = 20 cm2.
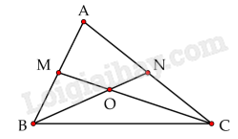
Cách giải:
Nối A với O
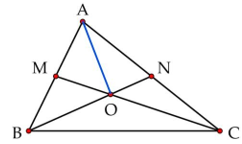
Vì M là trung điểm của AB nên AM = MB = $\frac{1}{2}$ AB nên:
${S_{BMO}} = \frac{1}{2} \times {S_{ABO}}$(Chung chiều cao từ O) nên SABO = 20 x 2 = 40 (cm2)
SBMO = SAMO (Chung chiều cao từ O)
SABN = SACM (Chung chiều cao từ O)
Suy ra SBCM – SBMO = SACM – SAMO hay SBCO = SACO = 40 cm2
Vì N là trung điểm của AC nên AN = NC = $\frac{1}{2}$ AC nên:
SAON = SCON (Chung chiều cao từ O)
SABN = SACM (Chung chiều cao từ O)
Suy ra SABN – SAON = SACM – SCON hay SABO = SBOC = 40 cm2
Diện tích tam giác ABC là 40 + 40 + 40 = 120 (cm2)
Đáp án: 120 cm2
PHẦN 2. TỰ LUẬN
Bài 1. Tìm x biết $x + 3,8 = 3,5 \times 1,5$
Cách giải
x + 3,8 = 3, 5 x 1, 5
x + 3,8 = 5, 25
x = 5, 25 - 3,8
x = 1, 45
Bài 2. Tổng số gạo bán cả 3 ngày là 125,6 tạ gạo. Số gạo bán ngày thứ ba hơn số gạo bán ngày thứ nhất và ngày thứ hai là 19 tạ gạo. Số gạo bán ngày thứ hai bằng 30% số gạo bán ngày thứ nhất. Hỏi mỗi ngày bán được bao nhiêu tạ gạo?
Cách giải:
Số gạo bán được trong ngày thứ ba là: (125,6 + 19) : 2 = 72,3 (tạ)
Số gạo bán được trong ngày thứ nhất và ngày thứ hai là: 125,6 - 72,3 = 53,3 (tạ)
Tỉ số của số gạo bán ngày thứ hai và số gạo bán ngày thứ nhất là 30% = $\frac{3}{{10}}$
Số gạo bán ngày thứ nhất là: 53, 3 : (3 + 10) x 10 = 41 (tạ)
Số gạo bán ngày thứ hai là: 53,3 – 41 = 12,3 (tạ)
Đáp số: Ngày thứ nhất: 41 tạ gạo
Ngày thứ hai: 12,3 tạ gạo
Ngày thứ ba: 72,3 tạ gạo
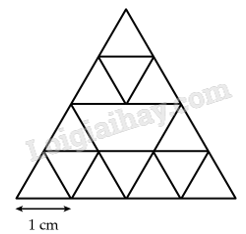
Bài 3. Cho hình vẽ bên.
a) Có bao nhiêu hình tam giác được cấu tạo bởi các hình tam giác có cạnh là 1 cm?
b) Xóa 2 đoạn 1 cm để được ít hình tam giác nhất.
Cách giải:
a) Có số tam giác được cấu tạo bởi các hình tam giác có cạnh là 1 cm là: 1 + 3 + 5 + 7 = 16 (hình tam giác)
b) Xóa hai đoạn thuộc đường chéo hoặc trung tâm của hình sẽ làm mất nhiều tam giác nhất.
Ví dụ như sau:
Các bài khác cùng chuyên mục
- Đề thi thử vào lớp 6 môn Toán trường chuyên Ngoại ngữ (đề số 7)
- Đề thi thử vào lớp 6 môn Toán trường chuyên Ngoại ngữ (đề số 6)
- Đề thi thử vào lớp 6 môn Toán trường chuyên Ngoại ngữ (đề số 5)
- Đề minh hoạ thi vào lớp 6 trường THCS và THPT Lương Thế Vinh năm học 2020 - 2021 (đề 3)
- Đề thi vào lớp 6 trường THCS Chu Văn An - Long Biên năm học 2022 - 2023
- Đề thi thử vào lớp 6 môn Toán trường chuyên Ngoại ngữ (đề số 7)
- Đề thi thử vào lớp 6 môn Toán trường chuyên Ngoại ngữ (đề số 6)
- Đề thi thử vào lớp 6 môn Toán trường chuyên Ngoại ngữ (đề số 5)
- Đề minh hoạ thi vào lớp 6 trường THCS và THPT Lương Thế Vinh năm học 2020 - 2021 (đề 3)
- Đề thi vào lớp 6 trường THCS Chu Văn An - Long Biên năm học 2022 - 2023













Danh sách bình luận