 Đề thi vào lớp 6 môn toán có đáp án - 9 năm gần nhất
Đề thi vào lớp 6 môn toán có đáp án - 9 năm gần nhất
 Đề thi vào lớp 6 môn Toán trường THCS Lê Văn Thiêm - Hà..
Đề thi vào lớp 6 môn Toán trường THCS Lê Văn Thiêm - Hà.. Đề thi vào lớp 6 môn Toán trường THCS Lê Văn Thiêm năm 2023
Tải về7 kg 50 g = 7 kg 50 g = ... kg, số thích hợp viết vào chỗ chấm (....) là: Số $overline {5a322} $ chia hết cho 9 khi a bằng: Tổng của hai số là 185 và hiệu của hai số đó là 63 . Vậy số bé là: Biết $frac{2}{3}$của một số có giá trị bằng 2,16. Số đó là: Khi viết thêm chữ số 1 vào bên trái của một số tự nhiên có hai chữ số thì số đó tăng thêm Số đơn vị là:
Đề thi
|
PHÒNG GD-ĐT HÀ TĨNH ĐỀ CHÍNH THỨC
|
BÀI KIỂM TRA ĐÁNH GIÁ NĂNG LỰC Tuyển sinh vào lớp 6, trường THCS Lê Văn Thiêm Năm học 2023-2024 Thời gian làm bài: 30 phút (không kể thời gian phát đề) |
A. PHẦN TRẮC NGHIỆM (7 điểm)
Học sinh ghi đáp án đúng (A, B, C hoặc D) từ câu 1 đến câu 14 vào tờ giấy kiểm tra.
Câu 1.
7 kg 50 g = 7 kg 50 g = ... kg, số thích hợp viết vào chỗ chấm (....) là:
A. 7,5
B. 7,05
C. 7,005
D. 750
Câu 2. Số $\overline {5a322} $ chia hết cho 9 khi a bằng:
A. 6
B. 7
C. 9
D. 8
Câu 3. Tổng của hai số là 185 và hiệu của hai số đó là 63 . Vậy số bé là:
A. 124
B. 56
C. 60
D. 61
Câu 4. Biết $\frac{2}{3}$của một số có giá trị bằng 2,16. Số đó là:
A. 1,44
B. 5,4
C. 3,24
D. 3,4
Câu 5. Khi viết thêm chữ số 1 vào bên trái của một số tự nhiên có hai chữ số thì số đó tăng thêm Số đơn vị là:
A. 1 000
B. 10
C. 100
D. 1
Câu 6.
Lúc 8 giờ, một ô tô đi từ A đến B với vận tốc 60 km/giờ và đến B lúc 10 giờ 30 phút cùng ngày. Độ dài quãng dường AB là:
A. 138 km
B. 150 km
C. 120 km
D. 90 km
Câu 7. Bác An thả một vật không thấm nước có dạng hình lập phương vào một chậu đựng đầy nước thì vật đó chìm hoàn toàn trong nước. Biết lượng nước tràn ra ngoài là 8 lít, vậy cạnh của vật hình lập phương đó là:
A. 8 dm
B. 4 dm
C. 0,2 dm
D. 2 dm
Câu 8. Bác Lan gửi vào ngân hàng 50 000 000 đồng với lãi suất 6% một năm. Hỏi sau hai năm, bác Lan nhận được tất cả bao nhiêu tiền? (Biết rằng, tiền lãi năm trước nhập thành gốc của năm sau).
A. 56 180 000 đồng
B. 56 000 000 đồng
C. 6 180 000 đồng
D. 53 180 000 đồng
Câu 9. Bạn Nam mua 3 quyển vở và 5 cái bút hết 55 000 đồng; mua 2 quyển vở và 8 cái bút như thế hết 60 000 đồng. Giá tiền của một cái bút đó là:
A. 4 000 đồng
B. 10 000 đồng
C. 5 000 đồng
D. 6 000 đồng
Câu 10. Một mảnh vườn hình chữ nhật có chiều dài 10 m, chiều rộng 8 m. Ở giữa vườn có làm một bồn hoa hình tròn có đường kính 4 m và lối đi có diện tích là 10 m2, phần đất còn lại dùng để trồng rau. Diện tích phần trồng rau đó là:
A. 57,44 m2
B. 67,44 m2
C. 19,76 m2
D. 29,76 m2
Câu 11. Cho tam giác ABC vuông tại A, AB = 6 cm; AC = 8 cm; BC = 10 cm. Chiều cao AH của tam giác ABC là:
A. 2,4 cm
B. 4,8 cm
C. 7,5 cm
D. 4 cm
Câu 12. Trong một hộp có 8 viên bi màu xanh, 10 viên bi màu đỏ, 12 viên bi màu tím, 15 viên bi màu vàng. Bạn Sơn không nhìn vào hộp mà bốc ra một số viên bi. Vậy số viên bi mà bạn Sơn Cần phải bốc ít nhất để chắc chắn trong số viên bi được bốc ra có đủ cả bốn màu xanh, đỏ, tím, vàng
A. 4
B. 31
C. 37
D. 38
Câu 13. Số hạng thứ 20 của dãy số 3; 4; 6; 9; 13; … là:
A. 190
B. 213
C. 196
D. 193
Câu 14. Mỗi hàng, mỗi cột của bảng sau là dãy số cách đều gồm 5 số hạng. Giá trị của 𝑥 là:
|
1 |
|
17 |
||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
17 |
|
|
|
49 |
A. 25
B. 21
C. 17
D. 29
B. PHẦN TỰ LUẬN (3 điểm):
Câu 15. Tính bằng cách thuận tiện nhất:
23,24 × 5,8 − 23,24 × 4,7 − 15,24 − 823,24 × 5,8 − 23,24 × 4,7 − 15,24 – 8
Câu 16.
Tìm số tự nhiên 𝑥 biết:
$\frac{{40}}{{17}} \times \frac{{34}}{{25}} < x < 4:0,5 - \frac{1}{4}:0,25 - \frac{1}{{10}}:0,1$
Câu 17.
a) Cho tam giác ABC, trên cạnh AC lấy diểm K sao cho AK=$\frac{1}{3}$ AC, trên cạnh AB lấy điểm I sao cho AI = $\frac{1}{3}$ AB. Nối IC và BK cắt nhau tại O. So sánh diện tích tam giác ABK và diện tích tam giác BCK.
b) Biết IC = 32 cm, tính độ dài đoạn thẳng IO.
c) Biết IC = 32 cm, tính độ dài đoạn thẳng OC.
------ HẾT ------
Đáp án
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1. 7 kg 50 g = 7 kg 50 g = ... kg, số thích hợp viết vào chỗ chấm (....) là:
A. 7,5
B. 7,05
C. 7,005
D. 750
Phương pháp
Áp dụng cách đổi: 1 g = $\frac{1}{{1000}}$kg
Lời giải
50 g = $\frac{{50}}{{1000}}$kg
7 kg 50 g = 7$\frac{{50}}{{1000}}$kg = 7,05 kg
Đáp án: B
Câu 2. Số $\overline {5a322} $chia hết cho 9 khi a bằng:
A. 6
B. 7
C. 9
D. 8
Phương pháp
Các số có tổng các chữ số chia hết cho 9 thì chia hết cho 9.
Lời giải
Số $\overline {5a322} $ có tổng các chữ số là 5 + a + 3 + 2 + 2 = 12 + a
Để $\overline {5a322} $chia hết cho 9 thì a = 6
Đáp án: A
Câu 3. Tổng của hai số là 185 và hiệu của hai số đó là 63 . Vậy số bé là:
A. 124
B. 56
C. 60
D. 61
Phương pháp
Số bé = (tổng – hiệu) : 2
Lời giải
Số bé là: (185 – 63) : 2 = 61
Đáp án: D
Câu 4. Biết $\frac{2}{3}$của một số có giá trị bằng 2,16. Số đó là:
A. 1,44
B. 5,4
C. 3,24
D. 3,4
Phương pháp
Muốn tìm một số khi biết giá trị phân số của số đó, ta lấy số đó chia cho phân số
Lời giải
Số đó là: 2,16 : $\frac{2}{3}$ = 3,24
Đáp án: C
Câu 5. Khi viết thêm chữ số 1 vào bên trái của một số tự nhiên có hai chữ số thì số đó tăng thêm số đơn vị là:
A. 1 000
B. 10
C. 100
D. 1
Phương pháp
Gọi số đó là $\overline {ab} $
Tìm số mới
Tìm hiệu của số mới và số ban đầu
Lời giải
Gọi số đó là $\overline {ab} $
Khi viết thêm chữ số 1 vào bên trái của một số đó, ta được số mới là: 1$\overline {ab} $ = 100 + $\overline {ab} $
Khi viết thêm chữ số 1 vào bên trái của một số tự nhiên có hai chữ số thì số đó tăng thêm số đơn vị là: 1$\overline {ab} $ - $\overline {ab} $ = 100 + $\overline {ab} $ - $\overline {ab} $ = 100
Vậy khi viết thêm chữ số 1 vào bên trái của một số tự nhiên có hai chữ số thì số đó tăng thêm 100 đơn vị
Đáp án: C
Câu 6. Lúc 8 giờ, một ô tô đi từ A đến B với vận tốc 60 km/giờ và đến B lúc 10 giờ 30 phút cùng ngày. Độ dài quãng dường AB là:
A. 138 km
B. 150 km
C. 120 km
D. 90 km
Phương pháp
Tính thời gian người đó đi hết quãng đường AB
Quãng đường = Vận tốc × Thời gian
Lời giải
Thời gian người đó đi hết quãng đường AB là:
10 giờ 30 phút - 8 giờ = 2 giờ 30 phút
Đổi 2 giờ 30 phút = 2,5 giờ
Độ dài quãng đường AB là:
60 × 2,5 = 150 (km)
Đáp án: B
Câu 7. Bác An thả một vật không thấm nước có dạng hình lập phương vào một chậu đựng đầy nước thì vật đó chìm hoàn toàn trong nước. Biết lượng nước tràn ra ngoài là 8 lít, vậy cạnh của vật hình lập phương đó là:
A. 8 dm
B. 4 dm
C. 0,2 dm
D. 2 dm
Phương pháp
Lượng nước tràn ra ngoài chính là thể tích của hình lập phương
Thể hình lập phương = Cạnh × Cạnh × Cạnh
Lời giải
Đổi 8 lít 8 dm3
Vì trước đó bể đầy nước nên thể tích của hình lập phương chính là lượng nước tràn ra ngoài và bằng 8 dm3
Vì 2 × 2 × 2 = 8
Nên cạnh của hình lập phương bằng 2 dm
Đáp án: D
Câu 8. Bác Lan gửi vào ngân hàng 50 000 000 đồng với lãi suất 6% một năm. Hỏi sau hai năm, bác Lan nhận được tất cả bao nhiêu tiền? (Biết rằng, tiền lãi năm trước nhập thành gốc của năm sau).
A. 56 180 000 đồng
B. 56 000 000 đồng
C. 6 180 000 đồng
D. 53 180 000 đồng
Phương pháp
Số tiền lãi bác Lan nhận được sau 1 năm = Số tiền bác Lan gửi × 6%
Số tiền bác Lan nhận được sau 1 năm = Số tiền bác Lan gửi + Số tiền lãi bác Lan nhận được sau 1 năm
Số tiền lãi bác Lan nhận được sau 2 năm = Số tiền bác Lan nhận được sau 1 năm × 6%
Số tiền bác Lan nhận được sau 2 năm = Số tiền bác Lan nhận được sau 1 năm + Số tiền lãi bác Lan nhận được sau 2 năm
Lời giải
Số tiền lãi bác Lan nhận được sau 1 năm là:
50 000 000 × 6% = 3 000 000 (đồng)
Số tiền bác Lan nhận được sau 1 năm là:
50 000 000 + 3 000 000 = 53 000 000 (đồng)
Số tiền lãi bác Lan nhận được sau 2 năm là:
53 000 000 × 6% = 3 180 000 (đồng)
Số tiền bác Lan nhận được sau 2 năm là:
53 000 000 + 3 180 000 = 56 180 000 (đồng)
Đáp án: A
Câu 9. Bạn Nam mua 3 quyển vở và 5 cái bút hết 55 000 đồng; mua 2 quyển vở và 8 cái bút như thế hết 60 000 đồng. Giá tiền của một cái bút đó là:
A. 4 000 đồng
B. 10 000 đồng
C. 5 000 đồng
D. 6 000 đồng
Phương pháp
- Giá tiền 1 quyển vở và 4 cái bút = Giá tiền mua 2 quyển vở và 8 cái bút : 2
- Giá tiền 2 quyển vở và 1 cái bút = Giá tiền mua 3 quyển vở và 5 cái bút - Giá tiền mua 1 quyển vở và 4 cái bút
- Giá tiền 7 cái bút = Giá tiền mua 2 quyển vở và 8 cái bút - Giá tiền mua 2 quyển vở và 1 cái bút
- Giá tiền 1 cái bút là:
- Giá tiền 7 cái bút : 7
Lời giải
Giá tiền 1 quyển vở và 4 cái bút là:
60 000 : 2 = 30 000 (đồng)
Giá tiền 2 quyển vở và 1 cái bút là:
55 000 – 30 000 = 25 000 (đồng)
Giá tiền 7 cái bút là:
60 000 – 25 000 = 35 000 (đồng)
Giá tiền 1 cái bút là:
35 000 : 7 = 5 000 (đồng)
Đáp án: C
Câu 10. Một mảnh vườn hình chữ nhật có chiều dài 10 m, chiều rộng 8 m. Ở giữa vườn có làm một bồn hoa hình tròn có đường kính 4 m và lối đi có diện tích là 10 m2, phần đất còn lại dùng để trồng rau. Diện tích phần trồng rau đó là:
A. 57,44 m2
B. 67,44 m2
C. 19,76 m2
D. 29,76 m2
Phương pháp
- Diện tích mảnh vườn hình chữ nhật = Chiều dài × Chiều rộng
- Diện tích bồn hoa hình tròn = Bán kính × Bán kính × 3,14
- Diện tích phần đất trồng rau = Diện tích mảnh vườn hình chữ nhật - Diện tích bồn hoa hình tròn – Diện tích lối đi
Lời giải
Diện tích mảnh vườn hình chữ nhật là:
10 × 8 = 80 (m2)
Diện tích bồn hoa hình tròn là:
$\frac{4}{2} \times \frac{4}{2} \times 3,14$ = 12,56 (m2)
Diện tích phần đất trồng rau là:
80 - 12,56 – 10 = 57,44 (m2)
Đáp án: A
Câu 11. Cho tam giác ABC vuông tại A, AB = 6 cm; AC = 8 cm; BC = 10 cm. Chiều cao AH của tam giác ABC là:
A. 2,4 cm
B. 4,8 cm
C. 7,5 cm
D. 4 cm
Phương pháp
Hình minh họa:
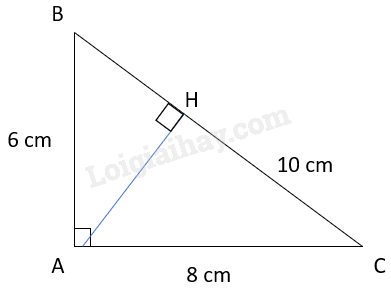
Diện tích hình tam giác ABC = AB × AC = AH × BC
Chiều cao hình tam giác = Diện tích : Độ dài cạnh đáy
Lời giải
Diện tích hình tam giác ABC là:
6 × 8 = 48 (cm2)
Chiều cao AH là:
48 : 10 = 4,8 (cm)
Đáp án: B
Câu 12. Trong một hộp có 8 viên bi màu xanh, 10 viên bi màu đỏ, 12 viên bi màu tím, 15 viên bi màu vàng. Bạn Sơn không nhìn vào hộp mà bốc ra một số viên bi. Vậy số viên bi mà bạn Sơn Cần phải bốc ít nhất để chắc chắn trong số viên bi được bốc ra có đủ cả bốn màu xanh, đỏ, tím, vàng
A. 4
B. 31
C. 37
D. 38
Phương pháp
Trường hợp xấu nhất khi chỉ bốc được 3 màu
Số viên bi khi chắc chắn bốc được 4 màu = Tổng số bi 3 của màu bi nhiều nhất + 1
Lời giải
Ngược lại với việc chắc chắn có đủ 4 màu là chúng ta chỉ bốc được bi của 3 màu. Như vậy trường hợp xấu nhất là ta bốc phải toàn bi của 3 màu mà có nhiều bi nhất (ở bài toán này là màu Vàng, màu Tím và màu Đỏ). Khi đó ta đã bốc: 15 + 12 + 10 = 37 viên mà vẫn không có đủ 4 màu => Ta bốc thêm 1 viên nữa chắc chắn sẽ có đủ 4 màu. Đáp án: 38 viên.
Đáp án: D
Câu 13. Số hạng thứ 20 của dãy số 3; 4; 6; 9; 13; … là:
A. 190
B. 213
C. 196
D. 193
Phương pháp
Tìm quy luật của dãy số
Dựa vào quy luật, tìm số hạng thứ 20 của dãy số
- Áp dụng công thức:
Số số hạng của dãy số = (Số hạng cuối – số hạng đầu) : khoảng cách + 1
Tổng của dãy số cách đều = (số hạng đầu + số hạng cuối) x số số hạng : 2
Lời giải
Số hạng thứ nhất là 3
Số hạng thứ 2 là: 3 + 1
Số hạng thứ 3 là: 3 + 1 + 2 = 3 + ( 1 + 2 + 3)
Số hạng thứ 4 là: 3 + 1 + 2 + 3 = 3 + ( 1 + 2 + 3 + 4)
Số hạng thứ 5 là: 3 + 1 + 2 + 3 + 4 = 3 + ( 1 + 2 + 3 + 4)
…
Vậy số hạng thứ 20 là: 3 + (1 + 2 + 3 + 4 + … + 19)
= 3 + (19 + 1) × 19 : 2 = 193
Đáp án: D
Câu 14. Mỗi hàng, mỗi cột của bảng sau là dãy số cách đều gồm 5 số hạng. Giá trị của 𝑥 là:
|
1 |
|
|
|
17 |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
17 |
|
|
|
49 |
A. 25
B. 21
C. 17
D. 29
Phương pháp
Vì mỗi hàng, mỗi cột của bảng sau là dãy số cách đều gồm 5 số hạng
- Cách 1: Áp dụng công thức:
Số số hạng của dãy số = (Số hạng cuối – số hạng đầu) : khoảng cách + 1
- Cách 2: Áp dụng cách tìm trung bình cộng của dãy số cách đều
Trung bình cộng = (số đầu + số cuối) : 2
(Nếu dãy số có lẻ số thì trung bình cộng là số chính giữa của dãy)
Lời giải
Vì mỗi hàng, mỗi cột của bảng sau là dãy số cách đều gồm 5 số hạng
- Cách 1: Áp dụng công thức:
Số số hạng của dãy số = (Số hạng cuối – số hạng đầu) : khoảng cách + 1
* Hàng ngang 1:
Số số hạng của dãy số = (Số hạng cuối – số hạng đầu) : khoảng cách + 1
5 = (17 – 1) : khoảng cách + 1
16 : khoảng cách = 5 – 1
16 : khoảng cách = 4
khoảng cách = 16 : 4 = 4. Vậy 2 số liên tiếp trong hàng ngang thứ nhất hơn kém nhau 4 đơn vị.
Ta điền được ở hàng ngang thứ nhất và hàng dọc thứ nhất như sau:
|
1 |
5 |
9 |
13 |
17 |
|
5 |
|
|
|
|
|
9 |
|
x |
|
|
|
13 |
|
|
|
|
|
17 |
|
|
|
49 |
* Hàng ngang 4:
5 = (49 – 17) : khoảng cách + 1
32 : khoảng cách = 5 – 1
32 : khoảng cách = 4
khoảng cách = 32 : 4 = 8
Vậy 2 số liên tiếp trong hàng ngang thứ 4 hơn kém nhau 4 đơn vị.
Ta điền được ở hàng ngang thứ 4 và hàng dọc thứ 4 như sau:
|
1 |
5 |
9 |
13 |
17 |
|
5 |
|
|
|
25 |
|
9 |
|
x |
|
33 |
|
13 |
|
|
|
41 |
|
17 |
25 |
33 |
41 |
49 |
* Hàng ngang 3:
5 = (33 – 9) : khoảng cách + 1
24 : khoảng cách = 5 – 1
24 : khoảng cách = 4
khoảng cách = 24 : 4 = 6
Vậy 2 số liên tiếp trong hàng ngang thứ 3 hơn kém nhau 6 đơn vị.
Ta điền được ở hàng ngang thứ 3 như sau:
|
1 |
5 |
9 |
13 |
17 |
|
5 |
|
|
|
25 |
|
9 |
15 |
21 |
27 |
33 |
|
13 |
|
27 |
|
41 |
|
17 |
25 |
33 |
41 |
49 |
Vậy x = 21
- Cách 2: Áp dụng cách tìm trung bình cộng của dãy số cách đều
* Hàng ngang 1:
Vì dãy số có 5 số nên trung bình cộng là số chính giữa của dãy.
Trung bình cộng = (1 + 17) : 2 = 9. Vậy ta điền được như sau:
|
1 |
|
9 |
|
17 |
|
|
|
|
|
|
|
9 |
|
x |
|
|
|
|
|
|
|
|
|
17 |
|
|
|
49 |
* Hàng ngang 4:
Vì dãy số có 5 số nên trung bình cộng là số chính giữa của dãy.
Trung bình cộng = (17 + 49) : 2 = 33. Vậy ta điền được như sau:
|
1 |
|
9 |
|
17 |
|
|
|
|
|
|
|
9 |
|
x |
|
33 |
|
|
|
|
|
|
|
17 |
|
33 |
|
49 |
* Hàng ngang 3:
Vì dãy số có 5 số nên trung bình cộng là số chính giữa của dãy.
Trung bình cộng (hay chính là giá trị của x) = (9 + 33) : 2 = 21. Vậy x = 21.
Đáp án: B
B. PHẦN TỰ LUẬN (3 điểm):
Câu 15. Tính bằng cách thuận tiện nhất:
23,24 × 5,8 − 23,24 × 4,7 − 15,24 – 8
Phương pháp
Áp dụng công thức:
a × b - a × c = a × (b - c)
Muốn nhân một số thập phân với 0,1 ta chỉ việc chuyển dấu phẩy của số đó sang bên trái chữ số.
Lời giải
23,24 × 5,8 − 23,24 × 4,7 − 15,24 – 8
23,24 × 5,8 − 23,24 × 4,7 − 23,24
= 23,24 × (5,8 − 4,7 - 1)
= 23,24 × 0,1
= 2,324
Câu 16.
Tìm số tự nhiên 𝑥 biết:
$\frac{{40}}{{17}} \times \frac{{34}}{{25}} < x < 4:0,5 - \frac{1}{4}:0,25 - \frac{1}{{10}}:0,1$
Phương pháp
- Muốn chia một số cho 0,25 ta chỉ việc nhân số đó với 4.
- Muốn chia một số cho 0,1 ta chỉ việc nhân số đó với 10.
- Muốn chia một số cho 0,5 ta chỉ việc nhân số đó với 2.
Lời giải
Ta có: $\frac{{40}}{{17}} \times \frac{{34}}{{25}} = \frac{{8 \times 5 \times 17 \times 2}}{{17 \times 5 \times 5}} = \frac{{8 \times 2}}{5} = \frac{{16}}{5}$= 3,2
$4:0,5 - \frac{1}{4}:0,25 - \frac{1}{{10}}:0,1 = 4 \times 2 - \frac{1}{4} \times 4 - \frac{1}{{10}} \times 10 = 8 - 1 - 1 = 6$
Vậy 3,2 < x < 6
x là số tự nhiên nên x = 4 hoặc x = 5
Câu 17.
a) Cho tam giác ABC, trên cạnh AC lấy diểm K sao cho AK=$\frac{1}{3}$ AC, trên cạnh AB lấy điểm I sao cho AI = $\frac{1}{3}$ AB. Nối IC và BK cắt nhau tại O. So sánh diện tích tam giác ABK và diện tích tam giác BCK.
b) Biết IC = 32 cm, tính độ dài đoạn thẳng IO.
c) Biết IC = 32 cm, tính độ dài đoạn thẳng OC.
Phương pháp
- Muốn tính diện tích hình tam giác ta lấy độ dài đáy nhân với chiều cao (cùng một đơn vị đo) rồi chia cho 2.
- Tìm mối liên hệ giữa đoạn thẳng IO, OC với đoạn thẳng IC dựa vào mối liên hệ giữa diện tích các hình tam giác chứa các cạnh đó. Sau đó tính độ dài đoạn thẳng IO, OC.
Lời giải
Ta có hình vẽ:
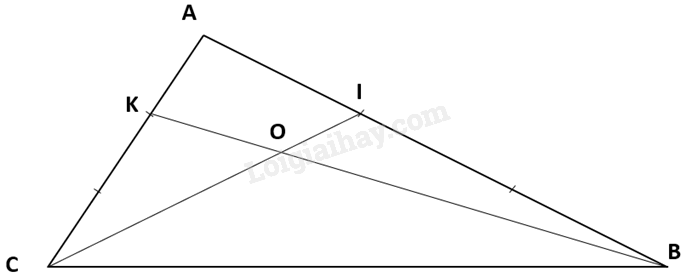
a) Kẻ đường cao BH từ B vuông góc với cạnh CA tại H.
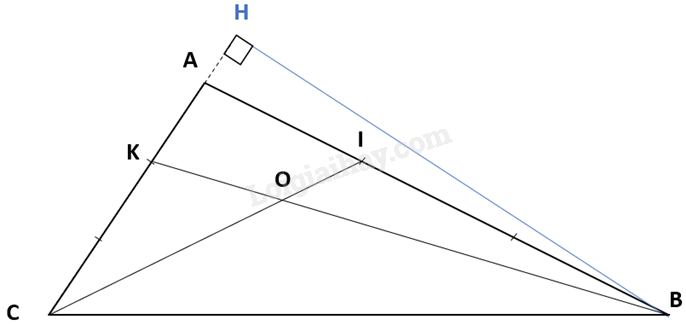
Ta có:
Diện tích tam giác ABK là: $\frac{{AK \times BH}}{2}$= AK × BH : 2
Theo đề ra, AK = $\frac{1}{3}$ AC hay KC = 2 × AK
Diện tích tam giác BCK là: $\frac{{KC \times BH}}{2}$= $\frac{{2 \times AK \times BH}}{2}$=$AK \times BH$
Vậy diện tích tam giác ABK bằng $\frac{1}{2}$ diện tích tam giác BCK
Vậy diện tích tam giác ABK bé hơn diện tích tam giác BCK.
b) Biết IC = 32 cm, tính độ dài đoạn thẳng IO.
Theo câu a), diện tích tam giác ABK bằng $\frac{1}{2}$ diện tích tam giác BCK = $\frac{1}{3}$diện tích tam giác ABC
Tương tự câu a), kẻ đường cao từ đỉnh C và vuông góc với cạnh BC.
Diện tích tam giác ACI bằng $\frac{1}{2}$ diện tích tam giác ICB = $\frac{1}{3}$diện tích tam giác ABC
Vậy diện tích tam giác ABK = Diện tích tam giác ACI (đều bằng $\frac{1}{3}$diện tích tam giác ABC)
Vậy diện tích tam giác KOC = Diện tích tam giác IOB (đều bằng $\frac{1}{3}$ diện tích tam giác ABC – diện tích tứ giác OKAI)
- Nối A với O
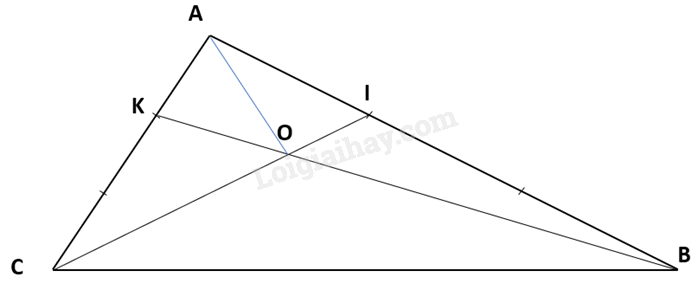
Diện tích tam giác OAK = $\frac{1}{2}$ diện tích tam giác KOC (Xét diện tích tam giác OAK và tam giác OKC có chung đường cao kẻ từ đỉnh O vuông góc với cạnh AC và cạnh đáy AK = $\frac{1}{2}$KC)
Diện tích tam giác IOA = $\frac{1}{2}$ diện tích tam giác IOB (Xét diện tích tam giác IOA và tam giác IOB có chung đường cao kẻ từ đỉnh O vuông góc với cạnh AB và cạnh đáy AI = $\frac{1}{2}$IB)
Vậy diện tích tam giác OAK = diện tích tam giác IOA (Vì diện tích tam giác KOC = diện tích tam giác IOB)
Ta có: Diện tích tam giác IOA = $\frac{1}{3}$ diện tích tam giác AOC (Vì diện tích tam giác KOC = diện tích tam giác IOB = $\frac{1}{2}$ diện tích tam giác KOC)
Xét tam giác IOA và tam giác AOC đều có chiều cao kẻ từ đỉnh A đến cạnh OC.
Vậy độ dài đáy IO = $\frac{1}{3}$ OC. Hay IO = $\frac{1}{4}$IC
Vậy độ dài IO là:
32 × $\frac{1}{4}$= 8 (cm)
c) Theo câu b, ta có độ dài IO = $\frac{1}{3}$ OC; IO = 8 cm
Vậy độ dài OC là:
8 : $\frac{1}{3}$= 24 (cm)
Đáp số: a) diện tích tam giác ABK bé hơn diện tích tam giác BCK
b) 8 cm
c) 24 cm
Các bài khác cùng chuyên mục
- Đề thi thử vào lớp 6 môn Toán trường chuyên Ngoại ngữ (đề số 7)
- Đề thi thử vào lớp 6 môn Toán trường chuyên Ngoại ngữ (đề số 6)
- Đề thi thử vào lớp 6 môn Toán trường chuyên Ngoại ngữ (đề số 5)
- Đề minh hoạ thi vào lớp 6 trường THCS và THPT Lương Thế Vinh năm học 2020 - 2021 (đề 3)
- Đề thi vào lớp 6 trường THCS Chu Văn An - Long Biên năm học 2022 - 2023
- Đề thi thử vào lớp 6 môn Toán trường chuyên Ngoại ngữ (đề số 7)
- Đề thi thử vào lớp 6 môn Toán trường chuyên Ngoại ngữ (đề số 6)
- Đề thi thử vào lớp 6 môn Toán trường chuyên Ngoại ngữ (đề số 5)
- Đề minh hoạ thi vào lớp 6 trường THCS và THPT Lương Thế Vinh năm học 2020 - 2021 (đề 3)
- Đề thi vào lớp 6 trường THCS Chu Văn An - Long Biên năm học 2022 - 2023












Danh sách bình luận