Đề thi vào lớp 6 môn Toán trường THCS Trần Mai Ninh thành phố Thanh Hoá năm 2025

Đề bài

Phần 1. Trắc nghiệm

Em hãy chọn chữ cái trước ý trả lời đúng

Câu 1 (1,5 điểm). Số 0,25 viết dưới dạng phân số thập phân là:

A. $\frac{{25}}{{10}}$                             B. $\frac{{25}}{{1000}}$            C. $\frac{{50}}{{200}}$                   D. $\frac{{25}}{{100}}$

Câu 2 (1,5 điểm). Số thập phân thích hợp viết vào chỗ chấm của 2 giờ 45 phút = ........ giờ là:
A. 2,25                       B. 2,45                       C. 2,75                       D. 165
Câu 3 (1,5 điểm). Trong hộp có 36 quả bóng, mỗi quả bóng nặng 7,8 g. Bạn Linh bỏ tất cả số bóng đó vào 1 chiếc hộp xanh và 1 chiếc hộp đỏ. Khi đó, Linh nhận thấy cân nặng của hộp xanh tăng thêm 148,2 g. Hỏi cân nặng của chiếc hộp đỏ tăng thêm bao nhiêu gam?
A. 132,6 g                  B. 280,8 g                  C. 140,4 g                  D. 148,2 g
Câu 4 (1,5 điểm). An có hai xúc xắc. Mỗi lần An gieo hai xúc xắc xuống bàn rồi ghi lại tổng số chấm ở mặt trên của hai xúc xắc đó. An cứ làm nhiều lần như vậy, hỏi An có thể ghi lại được nhiều nhất bao nhiêu tổng khác nhau?
A. 11 tổng                  B. 12 tổng                  C. 15 tổng                  D. 21 tổng

Câu 5 (2,0 điểm). Ghi kết quả các bài toán sau:
a) Rô-bốt nghĩ ra một số thập phân. Nếu dịch chuyển dấu phẩy của số đó sang trái một hàng thì được số mới kém số ban đầu là 18,225. Tìm số Rô-bốt đã nghĩ.
b) Năm nay, tổng số tuổi của ông nội, bố và Nam là 144 tuổi. Điều đặc biệt là 2 chữ số trong số tuổi của ông viết theo thứ tự ngược lại thì được tuổi của bố, cộng tất cả các chữ số trong tuổi của ông và bố thì được một số gấp đôi tuổi Nam. Tính tuổi Nam sau 3 năm nữa.

Phần II. Tự luận
Câu 6 (2,0 điểm). Trên bản đồ tỉ lệ 1 : 5 000, một hồ nước hình tròn có bán kính 1 cm. Hỏi trên thực tế, chu vi hồ nước là bao nhiêu mét?
Câu 7 (2,0 điểm). Tính giá trị của biểu thức $\frac{{17}}{9} \times \left( {8:\frac{{34}}{9}} \right) - \frac{{27}}{{15}}$

Câu 8 (3,0 điểm). Một ô tô khởi hành từ A với vận tốc 60 km/h và dự định tới B sau 3 giờ. Thực tế sau khi đi được 1 giờ 15 phút, xe bị hỏng nên phải dừng lại để sửa hết 15 phút. Hỏi muốn đến B đúng thời gian dự định thi trên đoạn đường còn lại ô tô phải đi với vận tốc là bao nhiêu km/h?

Câu 9 (3,0 điểm). Một trường tiểu học có 220 học sinh khối 4 và 180 học sinh khối 5. Cuối năm học có 30% số học sinh khối 4 đạt danh hiệu Học sinh xuất sắc và 25% số học sinh khối 5 đạt danh hiệu Học sinh xuất sắc. Hỏi cả hai khối 4 và 5, tỉ lệ học sinh đạt danh hiệu Học sinh xuất sắc là bao nhiêu phần trăm?
Câu 10 (2,0 điểm). Cho tam giác ABC, trên cạnh AC lấy điểm M sao cho AM = $\frac{1}{2}$MC.
Lấy O là trung điểm của BM. Nối A với O kéo dài cắt BC tại N.
a) Tính diện tích tam giác ABO, biết tam giác ABC có diện tích bằng 60 cm².
b) Tính tỉ số độ dài đoạn thẳng BN so với độ dài đoạn thẳng NC.

Đáp án

HƯỚNG DẪN GIẢI CHI TIẾT

Phần 1. Trắc nghiệm

Câu 1 (1,5 điểm). Số 0,25 viết dưới dạng phân số thập phân là:

A. $\frac{{25}}{{10}}$                             B. $\frac{{25}}{{1000}}$            C. $\frac{{50}}{{200}}$                   D. $\frac{{25}}{{100}}$

Cách giải

Số 0,25 viết dưới dạng phân số thập phân là: $\frac{{25}}{{100}}$

Đáp án: D

Câu 2 (1,5 điểm). Số thập phân thích hợp viết vào chỗ chấm của 2 giờ 45 phút = ........ giờ là:
A. 2,25                       B. 2,45                       C. 2,75                       D. 165

Cách giải

2 giờ 45 phút = 2 giờ + $\frac{{45}}{{60}}$ giờ = 2 giờ + 0,75 giờ = 2,75 giờ

Đáp án: C
Câu 3 (1,5 điểm). Trong hộp có 36 quả bóng, mỗi quả bóng nặng 7,8 g. Bạn Linh bỏ tất cả số bóng đó vào 1 chiếc hộp xanh và 1 chiếc hộp đỏ. Khi đó, Linh nhận thấy cân nặng của hộp xanh tăng thêm 148,2 g. Hỏi cân nặng của chiếc hộp đỏ tăng thêm bao nhiêu gam?
A. 132,6 g                  B. 280,8 g                  C. 140,4 g                  D. 148,2 g

Cách giải:

Số quả bóng bỏ vào chiếc hộp xanh là: 148,2 : 7,8 = 19 (quả)

Số quả bóng bỏ vào chiếc hộp đỏ là: 36 – 19 = 17 (quả)

Cân nặng của chiếc hộp đỏ tăng thêm số gam là: 7,8 x 17 = 132,6 (g)

Đáp án: A
Câu 4 (1,5 điểm). An có hai xúc xắc. Mỗi lần An gieo hai xúc xắc xuống bàn rồi ghi lại tổng số chấm ở mặt trên của hai xúc xắc đó. An cứ làm nhiều lần như vậy, hỏi An có thể ghi lại được nhiều nhất bao nhiêu tổng khác nhau?
A. 11 tổng                  B. 12 tổng                  C. 15 tổng                 D. 21 tổng

Cách giải

Số chấm trên mỗi mặt của xúc xắc là 1, 2, 3, 4, 5, 6 chấm.

Các trường hợp An có thể ghi được tổng khác nhau từ hai mặt trên của xúc xắc là:

1 và 2, 1 và 3, 1 và 4, 1 và 5, 1 và 6    (5 trường hợp)

2 và 3, 2 và 4, 2 và 5, 2 và 6      (4 trường hợp)

3 và 3, 3 và 5, 3 và 6      (3 tường hợp)

4 và 5, 4 và 6     (2 trường hợp)

5 và 6      (1 trường hợp)

Vậy có thể ghi được nhiều nhất 15 tổng khác nhau.

Đáp án: C

Câu 5 (2,0 điểm). Ghi kết quả các bài toán sau:
a) Rô-bốt nghĩ ra một số thập phân. Nếu dịch chuyển dấu phẩy của số đó sang trái một hàng thì được số mới kém số ban đầu là 18,225. Tìm số Rô-bốt đã nghĩ.

Cách giải:

Nếu dịch chuyển dấu phẩy của số đó sang trái một hàng thì số mới bằng $\frac{1}{{10}}$ số ban đầu.

Hiệu số phần bằng nhau là: 10 – 1 = 9 (phần)

Số ban đầu là 18,225 : 9 x 10 = 20,25

Đáp số: 20,25

b) Năm nay, tổng số tuổi của ông nội, bố và Nam là 144 tuổi. Điều đặc biệt là 2 chữ số trong số tuổi của ông viết theo thứ tự ngược lại thì được tuổi của bố, cộng tất cả các chữ số trong tuổi của ông và bố thì được một số gấp đôi tuổi Nam. Tính tuổi Nam sau 3 năm nữa.

Cách giải:

Gọi số tuổi của ông nội hiện nay là $\overline {ab} $ (a khác 0) thì số tuổi của bố là $\overline {ba} $ (b khác 0)

Gọi tuổi Nam hiện nay là c (c khác 0)

Theo đề bài tổng số tuổi của ông nội, bố và Nam là 144 tuổi nên:

$\overline {ab}  + \overline {ba}  + c = 144$

a x 10 + b + b x 10 + a + c = 144

a x 11 + b x 11 + c = 144

11 x (a + b) + c = 144             (1)

Ta có: Cộng tất cả các chữ số trong tuổi của ông và bố thì được một số gấp đôi tuổi Nam.

Suy ra (a + b + b + a) = 2 x c

            2 x (a + b) = 2 x c

                    a + b = c

Thay vào (1) ta có 11 x c + c = 144 hay 12 x c = 144

Suy ra c = 144 : 12 = 12

Tuổi Nam sau 3 năm nữa là 12 + 3 = 15 (tuổi)

Đáp số: 15 tuổi

Phần II. Tự luận
Câu 6 (2,0 điểm). Trên bản đồ tỉ lệ 1 : 5 000, một hồ nước hình tròn có bán kính 1 cm. Hỏi trên thực tế, chu vi hồ nước là bao nhiêu mét?

Cách giải:

Bán kính thực tế của hồ là:

1 x 5 000 = 5 000 (cm) = 50 m

Trên thực tế, chu vi hồ nước là

50 x 2 x 3,14 = 314 (m)

Đáp số: 314 m

Câu 7 (2,0 điểm). Tính giá trị của biểu thức $\frac{{17}}{9} \times \left( {8:\frac{{34}}{9}} \right) - \frac{{27}}{{15}}$

Cách giải:

$\frac{{17}}{9} \times \left( {8:\frac{{34}}{9}} \right) - \frac{{27}}{{15}}$

$ = \frac{{17}}{9} \times \left( {8 \times \frac{9}{{34}}} \right) - \frac{9}{5}$

$ = \frac{{17}}{9} \times \frac{{36}}{{17}} - \frac{9}{5}$

$ = 4 - \frac{9}{5}$

$ = \frac{{11}}{9}$

Câu 8 (3,0 điểm). Một ô tô khởi hành từ A với vận tốc 60 km/h và dự định tới B sau 3 giờ. Thực tế sau khi đi được 1 giờ 15 phút, xe bị hỏng nên phải dừng lại để sửa hết 15 phút. Hỏi muốn đến B đúng thời gian dự định thì trên đoạn đường còn lại ô tô phải đi với vận tốc là bao nhiêu km/h?

Cách giải:

Đổi: 1 giờ 5 phút = 1,25 giờ

         15 phút = 0,25 giờ

Thời gian ô tô dự định đi tiếp đến B là: 3 giờ - 1,25 giờ = 1,75 giờ

Vì phải dừng lại để sửa hết 15 phút nên muốn đến B đùng thời gian dự định thì trên đoạn đường còn lại ô tô phải đi trong thời gian là 1,75 giờ - 0,25 giờ = 1,5 giờ.

Gọi t₁, v₁ là thời gian và vận tốc dự định đi trên quãng đường còn lại.

Gọi t₂, v₂ là thời gian và vận tốc thực tế đi trên quãng đường còn lại.

Vì trên cùng một quãng đường, vận tốc và thời gian là hai đại lượng tỉ lệ nghịch nên:

$\frac{{{t_1}}}{{{t_2}}} = \frac{{{v_2}}}{{{v_1}}}$=$\frac{{1,75}}{{1,5}} = \frac{7}{6}$

Ta có v₁ = 60 km/h

Muốn đến B đúng thời gian dự định thì trên đoạn đường còn lại ô tô phải đi với vận tốc là:

v₂ = $60 \times \frac{7}{6} = 70$ (km/h)

Đáp số: 70 km/h

Câu 9 (3,0 điểm). Một trường tiểu học có 220 học sinh khối 4 và 180 học sinh khối 5. Cuối năm học có 30% số học sinh khối 4 đạt danh hiệu Học sinh xuất sắc và 25% số học sinh khối 5 đạt danh hiệu Học sinh xuất sắc. Hỏi cả hai khối 4 và 5, tỉ lệ học sinh đạt danh hiệu Học sinh xuất sắc là bao nhiêu phần trăm?

Cách giải:

Số học sinh xuất sắc của khối 4 là:

220 : 100 x 30 = 66 (học sinh)

Số học sinh xuất sắc của khối 5 là:

180 : 100 x 25 = 45 (học sinh)

Số học sinh khối 4 và 5 là:

220 + 180 = 400 (học sinh)

Tỉ lệ học sinh đạt danh hiệu Học sinh xuất sắc của hai khối 4 và 5 là:

(66 + 45) : 400 = 0,2775 = 27,75%

Đáp số: 27,75%

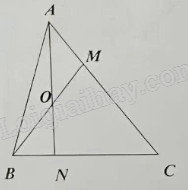
Câu 10 (2,0 điểm). Cho tam giác ABC, trên cạnh AC lấy điểm M sao cho AM = $\frac{1}{2}$MC.
Lấy O là trung điểm của BM. Nối A với O kéo dài cắt BC tại N.
a) Tính diện tích tam giác ABO, biết tam giác ABC có diện tích bằng 60 cm².
b) Tính tỉ số độ dài đoạn thẳng BN so với độ dài đoạn thẳng NC.

Cách giải:

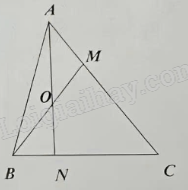
a) Ta có AM = $\frac{1}{2}$MC nên $AM = \frac{1}{3}AC$

$\frac{{{S_{ABM}}}}{{{S_{ABC}}}} = \frac{{AM}}{{AC}} = \frac{1}{3}$ (Hai tam giác có chung chiều cao hạ từ đỉnh B xuống đáy AC và đáy AM = $\frac{1}{3}$ AC)

Suy ra S_ABM = $\frac{1}{3}$ x S_ABC = $\frac{1}{3} \times 60 = 20$ (cm²)

$\frac{{{S_{ABO}}}}{{{S_{ABM}}}} = \frac{{BO}}{{BM}} = \frac{1}{2}$ (Hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy BM và đáy BO = $\frac{1}{2}$ BM)

Suy ra S_ABO = $\frac{1}{2}$ x S_ABM = $\frac{1}{2} \times 20 = 10$ (cm²)

b) Nối O với C

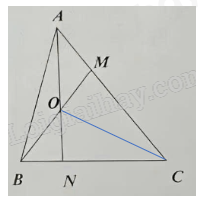
Ta có S_ABO = S_AOM (Hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy BM và đáy BO = OM)

S_AOM = $\frac{1}{3}$ S_AOC (Hai tam giác có chung chiều cao hạ từ đỉnh O xuống đáy AC và đáy AM = $\frac{1}{3}$ AC)

Suy ra S_ABO = $\frac{1}{3}$ S_AOC

Suy ra chiều cao hạ từ B xuống đáy AN = $\frac{1}{3}$ chiều cao hạ từ C xuống đáy AN

Suy ra S_ABN = $\frac{1}{3}$ S_ACN (Hai tam giác chung đáy AN)

Vậy BN = $\frac{1}{3}$ NC (chung chiều cao hạ từ A xuống đáy BC)