Đề thi vào lớp 6 môn Toán trường chuyên Ngoại ngữ năm 2021

Đề bài

ĐỀ THI VÀO LỚP 6 CHUYÊN NGOẠI NGỮ NĂM HỌC 2021 - 2022

MÔN: TOÁN

Câu 1. Cho phân số $\frac{{16}}{5}$. Nếu cộng thêm vào tử số và mẫu số của phân số đã cho cùng một số tự nhiên x thì ta được một phân số mới bằng 2. Hỏi $\frac{x}{2} + \frac{1}{{x - 1}}$ bằng bao nhiêu?

A. $\frac{{16}}{5}$                       

B. $\frac{7}{3}$                             

C. $\frac{{11}}{4}$                       

D. $\frac{{11}}{3}$

Câu 2. Gỗ tươi chứa 25% nước. Sau khi sấy, lượng nước trong gỗ khô là 4%. Hỏi khối lượng gỗ khô chiếm bao nhiêu phần trăm khối lượng gỗ tươi ban đầu?

A. 79%                    

B. 78,125%            

C. 80%                    

D. 76,875%

Câu 3. Trong kho nhà Minh có một số gạo, 10 ngày đầu nhà Minh dùng hết 1 yến gạo, 10 ngày tiếp theo nhà Minh dùng hết nửa số gạo còn lại, 10 ngày cuối tháng nhà Minh dùng hết số gạo trong kho và phải mua thêm 3 kg gạo nữa. Biết trong 30 ngày đó, nhà Minh dùng hết tất cả 0,35 tạ gạo. Hỏi 10 ngày cuối tháng, nhà Minh dùng hết bao nhiêu ki-lô-gam gạo?

A. 12 kg                  

B. 13 kg                   

C. 15 kg                  

D. 14 kg

Câu 4. Một hình hộp chữ nhật có chiều dài gấp hai lần chiều rộng. Nếu tăng chiều dài lên 5 dm và giữ nguyên chiều rộng, chiều cao thì thể tích hình hộp chữ nhật tăng lên 1,2 lần. Hỏi nếu tăng chiều rộng lên 5 dm, giảm chiều dài đi 5 dm và tăng chiều cao lên gấp đôi thì thể tích hình hộp chữ nhật tăng lên bao nhiêu lần?

A. 1,12 lần              

B. 2,24 lần              

C. 1,44 lần              

D. 2,28 lần

Câu 5. Cho hình thang ABCD có đáy CD gấp đôi đáy AB, hai đường chéo AC và BD cắt nhau tại điểm O. Điểm M nằm trên cạnh CD sao cho CM = $\frac{1}{3}$ CD. Gọi N là giao điểm của AC và BM. Biết diện tích hình thang ABCD là 45 cm², diện tích tam giác DON bằng bao nhiêu?

A. 15 cm²                

B. 10 cm²                

C. 8 cm²                  

D. 7 cm²

Câu 6. Hai lớp A và B mỗi lớp được phân công quét một nửa sân trường. Hai lớp bắt đầu quét cùng một lúc. Sau 20 phút lớp A quét xong nửa sân trường được phân cho lớp mình và tiếp tục sang quét cùng lớp B thêm 4 phút nữa thì hai lớp quét xong cả sân trường. Hỏi nếu lớp A không sang hỗ trợ thì lớp B sẽ quét hết nửa sân trường trong bao lâu?

A. 30 phút               

B. 25 phút               

C. 35 phút               

D. 40 phút

Đáp án

HƯỚNG DẪN GIẢI CHI TIẾT

Câu 1. Cho phân số $\frac{{16}}{5}$. Nếu cộng thêm vào tử số và mẫu số của phân số đã cho cùng một số tự nhiên x thì ta được một phân số mới bằng 2. Hỏi $\frac{x}{2} + \frac{1}{{x - 1}}$ bằng bao nhiêu?

A. $\frac{{16}}{5}$                       

B. $\frac{7}{3}$                             

C. $\frac{{11}}{4}$                       

D. $\frac{{11}}{3}$

Cách giải

Nếu cộng thêm vào tử số và mẫu số của phân số đã cho cùng một số tự nhiên x thì hiệu giữa tử số và mẫu số của phân số mới không đổi là 16 – 5 = 11

Lại có phân số mới bằng 2 nên tỉ số của tử số mới và mẫu số mới là 2 : 1

Ta có sơ đồ:

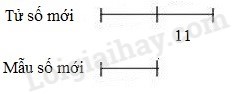
Mẫu số mới là 11 $ \Rightarrow $ 5 + x = 11 $ \Rightarrow $ x = 6

Ta có $\frac{x}{2} + \frac{1}{{x - 1}} = \frac{6}{2} + \frac{1}{{6 - 1}} = 3 + \frac{1}{5} = \frac{{16}}{5}$

Chọn A

Câu 2. Gỗ tươi chứa 25% nước. Sau khi sấy, lượng nước trong gỗ khô là 4%. Hỏi khối lượng gỗ khô chiếm bao nhiêu phần trăm khối lượng gỗ tươi ban đầu?

A. 79%                    

B. 78,125%            

C. 80%                    

D. 76,875%

Cách giải

Giả sử có 100 tấn gỗ tươi.

Lượng nước có trong 100 tấn gỗ tươi là 100 x 25 : 100 = 25 (tấn)

Khối lượng gỗ có trong 100 tấn gỗ tươi là 100 – 25 = 75 (tấn)

Khi lượng nước bay hơi thì khối lượng gỗ không thay đổi. Sau khi sấy, khối lượng gỗ chiếm:

100% - 4% = 96% (khối gỗ khô)

Khối lượng gỗ sau khi sấy 100 tấn gỗ tươi là 75 : 96 x 100 = 71,825 (tấn)

Vậy tỉ số phần trăm giữa khối lượng gỗ khô và khối lượng gỗ tươi ban đầu là:

71,825 : 100 x 100% = 71,825%

             Đáp số: 71,825%

Chọn B

Câu 3. Trong kho nhà Minh có một số gạo, 10 ngày đầu nhà Minh dùng hết 1 yến gạo, 10 ngày tiếp theo nhà Minh dùng hết nửa số gạo còn lại, 10 ngày cuối tháng nhà Minh dùng hết số gạo trong kho và phải mua thêm 3 kg gạo nữa. Biết trong 30 ngày đó, nhà Minh dùng hết tất cả 0,35 tạ gạo. Hỏi 10 ngày cuối tháng, nhà Minh dùng hết bao nhiêu ki-lô-gam gạo?

A. 12 kg                  

B. 13 kg                   

C. 15 kg                  

D. 14 kg

Cách giải

Đổi 1 yến = 10 kg, 0,35 tạ = 35 kg

Trong kho nhà Minh ban đầu có số gạo là 35 – 3 = 32 (kg)

Sau mười ngày đầu, số gạo còn lại là 32 – 10 = 22 (kg)

Mười ngày tiếp theo, nhà Minh dùng số gạo là 22 : 2 = 11 (kg)

Mười ngày cuối tháng, nhà Minh dùng số gạo là 35 – 10 – 11 = 14 (kg)

               Đáp số: 14 kg

Chọn D

Câu 4. Một hình hộp chữ nhật có chiều dài gấp hai lần chiều rộng. Nếu tăng chiều dài lên 5 dm và giữ nguyên chiều rộng, chiều cao thì thể tích hình hộp chữ nhật tăng lên 1,2 lần. Hỏi nếu tăng chiều rộng lên 5 dm, giảm chiều dài đi 5 dm và tăng chiều cao lên gấp đôi thì thể tích hình hộp chữ nhật tăng lên bao nhiêu lần?

A. 1,12 lần              

B. 2,24 lần              

C. 1,44 lần              

D. 2,28 lần

Cách giải

V_{ban đầu} = chiều dài x chiều rộng x chiều cao

Nếu tăng chiều dài lên 5 dm và giữ nguyên chiều rộng, chiều cao thì:

V₁ = (chiều dài + 5) x chiều rộng x chiều cao

      = (chiều rộng x 2 + 5) x chiều rộng x chiều cao

Theo đề bài V₁ = 1,2 x V_{ban đầu}

$ \Rightarrow $ (chiều rộng x 2 + 5) x chiều rộng x chiều cao = 1,2 x chiều rộng x 2 x chiều rộng x chiều cao

$ \Rightarrow $ chiều rộng x 2 + 5 = 1,2 x chiều rộng x 2

     chiều rộng x 2 + 5 = 2,4 x chiều rộng

     5 = (2,4 – 2) x chiều rộng

     5 = 0,4 x chiều rộng

$ \Rightarrow $ chiều rộng = 5 : 0,4 = 12,5 (cm)

Chiều dài là 12,5 x 2 = 25 (cm)

Khi đó V_{ban đầu} = 25 x 12,5 x chiều cao = 312,5 x chiều cao

Theo đề bài V₂ = (25 – 5) x (12,5 + 5) x chiều cao x 2 = 700 x chiều cao

Vậy lúc sau thể tích hình hộp chữ nhật đó tăng lên số lần là

                      700 : 312,5 = 2,24 (lần)

                                 Đáp số: 2,24 lần

Chọn B

Câu 5. Cho hình thang ABCD có đáy CD gấp đôi đáy AB, hai đường chéo AC và BD cắt nhau tại điểm O. Điểm M nằm trên cạnh CD sao cho CM = $\frac{1}{3}$ CD. Gọi N là giao điểm của AC và BM. Biết diện tích hình thang ABCD là 45 cm², diện tích tam giác DON bằng bao nhiêu?

A. 15 cm²                

B. 10 cm²                

C. 8 cm²                  

D. 7 cm²

Cách giải

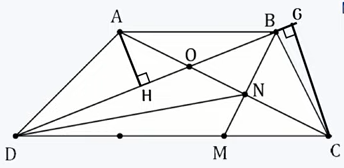
$\frac{{{S_{ABD}}}}{{{S_{BDC}}}} = \frac{1}{2}$ (chiều cao bằng nhau, đáy AB = $\frac{1}{2}$ đáy CD)

Mà S_ABD + S_BDC = S_ABCD = 45 cm²

S_ABD = 45 : (1 + 3) = 15 cm²

S_BDC = 45 – 15 = 30 cm²

$\frac{{{S_{ABD}}}}{{{S_{BDC}}}} = \frac{{AH}}{{CG}}$ (chung đáy BD) $ \Rightarrow \frac{{AH}}{{CG}} = \frac{1}{2}$ hay CG = AH x 2

S_ABD = S_ABC (chiều cao bằng nhau, chung đáy AB)

Mà S_ABD = S_ABO + S_AOD

      S_ABC = S_ABO + S_BOC

$ \Rightarrow $ S_AOD = S_BOC $ \Rightarrow $$\frac{{AH \times OD}}{2} = \frac{{CG \times OB}}{2}$

$ \Rightarrow $ AH x OD = AH x 2 x OB

$ \Rightarrow $ OD = 2 x OB hay OB = $\frac{1}{2}$ x OD

$\frac{{{S_{BOC}}}}{{{S_{DOC}}}} = \frac{1}{2}$ (chung chiều cao, đáy OB = $\frac{1}{2}$ đáy OD)

Mà S_BOC + S_DOC = S_BDC = 30 cm²

$ \Rightarrow $ S_DOC = 30 : (1 + 2) x 2 = 20 cm²

$\frac{{{S_{DBM}}}}{{{S_{BDC}}}} = \frac{2}{3}$ (chung chiều cao, đáy DM = $\frac{2}{3}$ đáy CD)

 $ \Rightarrow $ S_DBM = $\frac{2}{3} \times 30 = 20$cm² $ \Rightarrow $ S_DOC = S_DBM

Mà S_DOC = S_DOMN + S_MNC ; S_DBM = S_DOMN + S_BON

$ \Rightarrow $S_MNC = S_BON

Lại có $\frac{{{S_{MNC}}}}{{{S_{DMN}}}} = \frac{1}{2}$ (chung chiều cao, đáy CM = $\frac{1}{2}$ đáy DM)

           $\frac{{{S_{BON}}}}{{{S_{DON}}}} = \frac{1}{2}$ (chung chiều cao, đáy OB = $\frac{1}{2}$ đáy OD)

$ \Rightarrow $S_DMN = S_DON = S_MNC x 2

Mà S_DOC = S_DMN + S_DON + S_MNC = S_MNC x 5 = 20 cm²

$ \Rightarrow $S_MNC = 20 : 5 = 4 cm²

Vậy S_DON = 4 x 2 = 8 cm²

                Đáp số: 8 cm²

Chọn C

Câu 6. Hai lớp A và B mỗi lớp được phân công quét một nửa sân trường. Hai lớp bắt đầu quét cùng một lúc. Sau 20 phút lớp A quét xong nửa sân trường được phân cho lớp mình và tiếp tục sang quét cùng lớp B thêm 4 phút nữa thì hai lớp quét xong cả sân trường. Hỏi nếu lớp A không sang hỗ trợ thì lớp B sẽ quét hết nửa sân trường trong bao lâu?

A. 30 phút               

B. 25 phút               

C. 35 phút               

D. 40 phút

Cách giải:

Trong 4 phút, lớp A quét được $4:20 = \frac{1}{5}$ (nửa sân trường)

Lớp B quét được $1 - \frac{1}{5} = \frac{4}{5}$ (nửa sân trường)

Thời gian lớp B quét được $\frac{4}{5}$ nửa sân trường là: 20 phút + 4 phút = 24 phút

Vậy nếu lớp A không sang hỗ trợ thì lớp B sẽ quét hết nửa sân trường trong:

                                                $24:\frac{4}{5} = 30$ (phút)

                                                          Đáp số: 30 phút