 Đề thi vào lớp 6 môn toán có đáp án - 9 năm gần nhất
Đề thi vào lớp 6 môn toán có đáp án - 9 năm gần nhất
 Đề thi vào lớp 6 môn Toán trường Ngôi Sao - Hà Nội
Đề thi vào lớp 6 môn Toán trường Ngôi Sao - Hà Nội Đề thi vào lớp 6 môn Toán trường Ngôi sao năm 2021
Tải vềMột cửa hàng bán vải ngày thứ nhất bán được 32,7m, ngày thứ hai bán nhiều hơn ngày thứ nhất 4,6m ... Hình vẽ trên mô tả bàn cờ vua có kích thước 8 x 8. Quân Mã ban đầu đứng ở ô có chữ “M”.
Đề bài
ĐỀ THI HỌC BỔNG NGÔI SAO MÔN TOÁN VÀO LỚP 6 TRƯỜNG NGÔI SAO HÀ NỘI
NĂM HỌC 2021 – 2022
Thời gian làm bài: 60 phút
PHẦN 1. TRẮC NGHIỆM
Câu 1. Tính $\left( {4\frac{2}{5} + 2\frac{3}{7}} \right) + \left( {5\frac{4}{7} - 2\frac{2}{5}} \right)$
Câu 2. Biểu thức thích hợp để điền vào chỗ chấm sau là:
15,02 = ……
A. $10 + 5 + \frac{2}{{1000}}$
B. $10 + 2 + \frac{2}{{100}}$
C. $10 + \frac{5}{2} + \frac{2}{{100}}$
D. $10 + 5 + \frac{2}{{100}}$
Câu 3. Một cửa hàng bán vải ngày thứ nhất bán được 32,7m, ngày thứ hai bán nhiều hơn ngày thứ nhất 4,6m. Ngày thứ ba bán được số vải bằng trung bình cộng số vải của hai ngày đầu. Hỏi cả ba ngày cửa hàng đó bán được bao nhiêu mét vải?
Câu 4. Một nhóm học sinh cộng ngày và tháng sinh nhật của mỗi bạn lại thì thấy kết quả đều bằng 35. Biết rằng tất cả các ngày sinh nhật của họ là khác nhau. Hỏi nhóm học sinh đó có nhiều nhất bao nhiêu em?
Câu 5. Hình vẽ trên mô tả bàn cờ vua có kích thước 8 x 8. Quân Mã ban đầu đứng ở ô có chữ “M”. Hỏi sau 15 nước di chuyển trên bàn cờ, quân Mã đứng ở ô có màu gì? Biết con Mã đi theo đường chéo của hình chữ nhật 2 x 3.

Chọn đáp án đúng:
A. Không xác định được do tùy cách đi.
B. Màu trắng.
C. Màu đen.
D. Cả ba đáp án đều sai
Câu 6. Hai người thợ cùng nhận làm chung một công việc sau 8 ngày thì xong. Nhưng sau 5 ngày cùng làm thì người thứ nhất bận không làm tiếp được nữa. Một mình người thứ hai phải làm thêm 9 ngày nữa mới xong phần công việc còn lại. Hỏi một mình người thứ nhất làm công việc đó trong bao lâu thì xong?
Câu 7. Trong một buổi họp nhóm. Một bạn trai tên là Hùng nhận thấy mình có số bạn trai bằng số bạn gái. Một bạn gái tên là Mai nhận thấy mình có số bạn gái chỉ bằng một nửa số bạn trai. Hỏi nhóm đó có bao nhiêu bạn?
Câu 8. Một ô tô phải chạy từ A đến B. Sau khi chạy được 1 giờ thì ô tô giảm vận tốc chỉ còn bằng $\frac{5}{6}$ vận tốc ban đầu. Vì thế, ô tô đến B chậm mất 1 giờ 24 phút. Nếu từ A, sau khi chạy được 1 giờ, ô tô chạy thêm 50 km nữa rồi mới giảm vận tốc thì ô tô đến B chỉ chậm 1 giờ 12 phút. Tính quãng đường AB.
Câu 9. Hình bên dưới được xếp bởi các hình lập phương có cạnh 1 cm. Tính diện tích toàn phần của hình đó.
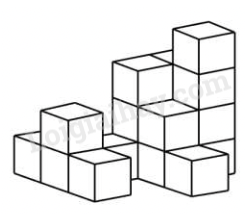
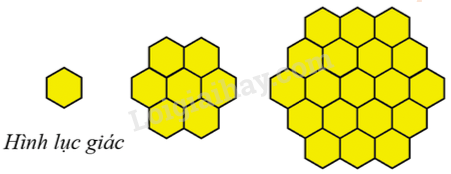
Câu 10. Quan sát các hình vẽ dưới đây để xác định hình thứ 222 có bao nhiêu hình lục giác?
PHẦN 2. TỰ LUẬN
Câu 1. Tìm $x$ biết:
a) $x \times 1,2 + x \times 0,7 = 61,94$
b) $\frac{1}{{3 \times 10}} + \frac{1}{{10 \times 17}} + \frac{1}{{17 \times 24}} + .... + \frac{1}{{(7 \times x + 10) \times (7 \times x + 3)}} = \frac{{13}}{{282}}$
Bài 2. Khi trả bài kiểm tra cuối học kì I môn Toán, cô giáo nói: “Số điểm 10 chiếm 25%, số điểm 9 hơn điểm 10 là 6,25%. Như vậy có 18 bạn được điểm 9 hoặc 10, tất cả học sinh trong lớp đều nộp bài kiểm tra”. Hỏi:
a) Số học sinh đạt điểm 9 chiếm bao nhiêu phần trăm số học sinh cả lớp?
b) Tổng số học sinh điểm 9 hoặc 10 chiếm bao nhiêu phần trăm số học sinh cả lớp?
c) Lớp đó có tất cả bao nhiêu học sinh?
d) Lớp đó có bao nhiêu học sinh không đạt điểm 9 hoặc 10?
Bài 3. Cho hình thang ABCD có đáy bé AB bằng $\frac{1}{3}$ đáy lớn. Chiều cao bằng 12,6m và bằng hiệu độ dài hai đáy.
a) Tính diện tích hình thang ABCD.
b) Hai đường chéo AC và BD cắt nhau tại O. So sánh SOBC và SOAD.
c) Kéo dài cạnh DA và CB cắt nhau tại P. Tính tỉ số diện tích của hai tam giác DBP và DPC.
Đáp án
HƯỚNG DẪN GIẢI CHI TIẾT
PHẦN 1. TRẮC NGHIỆM
Câu 1. Tính $\left( {4\frac{2}{5} + 2\frac{3}{7}} \right) + \left( {5\frac{4}{7} - 2\frac{2}{5}} \right)$
Cách giải:
Câu 2. Biểu thức thích hợp để điền vào chỗ chấm sau là:
15,02 = ……
A. $10 + 5 + \frac{2}{{1000}}$
B. $10 + 2 + \frac{2}{{100}}$
C. $10 + \frac{5}{2} + \frac{2}{{100}}$
D. $10 + 5 + \frac{2}{{100}}$
Cách giải:
$15,02 = 10 + 5 + 0,02 = 10 + 5 + \frac{2}{{100}}$
Chọn D
Câu 3. Một cửa hàng bán vải ngày thứ nhất bán được 32,7m, ngày thứ hai bán nhiều hơn ngày thứ nhất 4,6m. Ngày thứ ba bán được số vải bằng trung bình cộng số vải của hai ngày đầu. Hỏi cả ba ngày cửa hàng đó bán được bao nhiêu mét vải?
Cách giải:
Ngày thứ hai cửa hàng bán được số mét vải là:
32,7 + 4,6 = 37,3 (m)
Ngày thứ ba cửa hàng bán được số mét vải là:
(32,7 + 37,3) : 2 = 35 (m)
Cả ba ngày cửa hàng đó bán được số mét vải là:
32,7 + 37,3 + 35 = 105 (m)
Đáp số: 105 m vải
Câu 4. Một nhóm học sinh cộng ngày và tháng sinh nhật của mỗi bạn lại thì thấy kết quả đều bằng 35. Biết rằng tất cả các ngày sinh nhật của họ là khác nhau. Hỏi nhóm học sinh đó có nhiều nhất bao nhiêu em?
Cách giải:
Ta có khi cộng ngày và tháng sinh nhật của mỗi bạn lại thì thấy kết quả đều bằng 35
Vậy ngày sinh nhật của các học sinh đó có thể là:
23/12 ; 24/11 ; 25/10 ; 26/9 ; 27/8 ; 28/7 ; 29/6 ; 30/5
Vậy nhóm học sinh đó có nhiều nhất 8 em.
Câu 5. Hình vẽ trên mô tả bàn cờ vua có kích thước 8 x 8. Quân Mã ban đầu đứng ở ô có chữ “M”. Hỏi sau 15 nước di chuyển trên bàn cờ, quân Mã đứng ở ô có màu gì? Biết con Mã đi theo đường chéo của hình chữ nhật 2 x 3.

Chọn đáp án đúng:
A. Không xác định được do tùy cách đi.
B. Màu trắng.
C. Màu đen.
D. Cả ba đáp án đều sai
Cách giải:
Ban đầu con Mã đang đứng ở ô trắng, mà con Mã đi theo đường chéo của hình chữ nhật 2 x 3 nên nước di chuyển tiếp theo con Mã sẽ di chuyển vào ô đen.
Tương tự như vậy, nước di chuyển thứ hai con Mã sẽ di chuyển vào ô trắng. Vậy cứ qua 2 lần di chuyển, con Mã sẽ quay trở về ô màu trắng. Mà 15 : 2 = 7 (dư 1) nên ở nước di chuyển thứ 14, con Mã sẽ di chuyển vào ô màu trắng.
Vậy ở nước di chuyển thứ 15, con Mã sẽ di chuyển vào ô màu đen.
Chọn C
Câu 6. Hai người thợ cùng nhận làm chung một công việc sau 8 ngày thì xong. Nhưng sau 5 ngày cùng làm thì người thứ nhất bận không làm tiếp được nữa. Một mình người thứ hai phải làm thêm 9 ngày nữa mới xong phần công việc còn lại. Hỏi một mình người thứ nhất làm công việc đó trong bao lâu thì xong?
Cách giải:
Trong 1 ngày 2 người thợ làm chung được số phần công việc là $1:8 = \frac{1}{8}$ (công việc)
Trong 5 ngày 2 người thợ làm chung được số phần công việc là $\frac{5}{8}$ (công việc)
Số phần công việc người thứ hai làm trong 9 ngày là $1 - \frac{5}{8} = \frac{3}{8}$ (công việc)
Trong 1 ngày, người thứ hai làm được số phần công việc là: $\frac{3}{8}:9 = \frac{1}{{24}}$ (công việc)
Trong 1 ngày, người thứ nhất làm được số phần công việc là: $\frac{1}{8} - \frac{1}{{24}} = \frac{1}{{12}}$(công việc)
Một mình người thứ nhất làm công việc đó trong số ngày là: $1:\frac{1}{{12}} = 12$ (ngày)
Đáp số: 12 ngày
Câu 7. Trong một buổi họp nhóm. Một bạn trai tên là Hùng nhận thấy mình có số bạn trai bằng số bạn gái. Một bạn gái tên là Mai nhận thấy mình có số bạn gái chỉ bằng một nửa số bạn trai. Hỏi nhóm đó có bao nhiêu bạn?
Cách giải:
Hùng nhận thấy mình có số bạn trai bằng số bạn gái
$ \Rightarrow $ Số bạn trai trong nhóm nhiều hơn số bạn gái là 1 bạn.
Khi đó, số bạn gái của Mai kém số bạn trai của Mai là 2 bạn.
Số bạn gái của Mai là: 2 : (2 – 1) x 1 = 2 (bạn)
Số bạn trai của Mai là: 2 + 2 = 4 (bạn)
Nhóm có số bạn là: 2 + 4 + 1 = 7 (bạn)
Đáp số: 7 bạn
Câu 8. Một ô tô phải chạy từ A đến B. Sau khi chạy được 1 giờ thì ô tô giảm vận tốc chỉ còn bằng $\frac{5}{6}$ vận tốc ban đầu. Vì thế, ô tô đến B chậm mất 1 giờ 24 phút. Nếu từ A, sau khi chạy được 1 giờ, ô tô chạy thêm 50 km nữa rồi mới giảm vận tốc thì ô tô đến B chỉ chậm 1 giờ 12 phút. Tính quãng đường AB.
Cách giải:
Giả sử từ A ô tô chạy được 1 giờ đến C, rồi từ C chạy thêm 50 km nữa đến D mới giảm vận tốc thì thời gian đến B ít hơn là:
1 giờ 24 phút – 1 giờ 12 phút = 12 phút = 0,2 (giờ)
Vì ô tô giảm vận tốc bằng $\frac{5}{6}$ vận tốc ban đầu và thời gian tỉ lệ nghịch với vận tốc nên thời gian ô tô đi quãng đường CD với vận tốc ban đầu bằng $\frac{5}{6}$ thời gian ô tô đi với vận tốc mới.
Thời gian ô tô đi quãng đường CD với vận tốc ban đầu là:
0,2 : (6 – 5) x 5 = 1 (giờ)
Vận tốc của ô tô là:
50 : 1 = 50 (km/giờ)
Đổi: 1 giờ 24 phút = 1,4 giờ
Sau khi chạy được 1 giờ thì ô tô giảm vận tốc chỉ còn bằng $\frac{5}{6}$ vận tốc ban đầu thì ô tô đến B chậm mất 1 giờ 24 phút.
Vậy thời gian ô tô đi hết quãng đường CB là:
1,4 : (6 – 5) x 5 = 7 (giờ)
Độ dài quãng đường AB là:
50 x (7 + 1) = 400 (km)
Đáp số: 400 km
Câu 9. Hình bên dưới được xếp bởi các hình lập phương có cạnh 1 cm. Tính diện tích toàn phần của hình đó.

Cách giải:
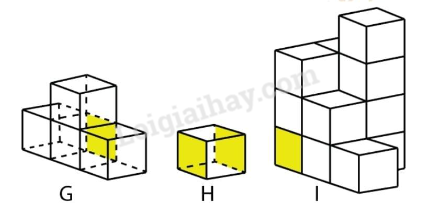
Chia hình đã cho thành ba hình G, H, I như hình vẽ.
Diện tích toàn phần của hình đã cho bằng tổng diện tích toàn phần của ba hình G, H, I trừ đi diện tích các mặt vàng.
Diện tích toàn phần của hình G bằng 18 cm2.
Diện tích toàn phần của hình H bằng 6 cm2.
Diện tích toàn phần của hình I bằng 40 cm2.
Vậy diện tích hình đã cho là: 18 + 6 + 40 – 4 = 60 (cm2)
Câu 10. Quan sát các hình vẽ dưới đây để xác định hình thứ 222 có bao nhiêu hình lục giác?

Cách giải:
Quy luật:
Số hình lục giác của hình thứ n bằng 1 + 6 x [0 + 1 + 2 + …. + (n – 1)]
Số hình lục giác của hình thứ 222 là: 1 + 6 x [0 + 1 + 2 + …. + 221] = 147187 (hình)
PHẦN 2. TỰ LUẬN
Câu 1. Tìm $x$ biết:
a) $x \times 1,2 + x \times 0,7 = 61,94$
b) $\frac{1}{{3 \times 10}} + \frac{1}{{10 \times 17}} + \frac{1}{{17 \times 24}} + .... + \frac{1}{{(7 \times x + 10) \times (7 \times x + 3)}} = \frac{{13}}{{282}}$
Cách giải:
a) $x \times 1,2 + x \times 0,7 = 61,94$
$x \times (1,2 + 0,7) = 61,94$
$x \times 1,9 = 61,94$
$x = 61,94:1,9$
$x = 32,6$
Bài 2. Khi trả bài kiểm tra cuối học kì I môn Toán, cô giáo nói: “Số điểm 10 chiếm 25%, số điểm 9 hơn điểm 10 là 6,25%. Như vậy có 18 bạn được điểm 9 hoặc 10, tất cả học sinh trong lớp đều nộp bài kiểm tra”. Hỏi:
a) Số học sinh đạt điểm 9 chiếm bao nhiêu phần trăm số học sinh cả lớp?
b) Tổng số học sinh điểm 9 hoặc 10 chiếm bao nhiêu phần trăm số học sinh cả lớp?
c) Lớp đó có tất cả bao nhiêu học sinh?
d) Lớp đó có bao nhiêu học sinh không đạt điểm 9 hoặc 10?
Cách giải
a) Số học sinh đạt điểm 9 chiếm:
25% + 6,25% = 31,25% (số học sinh cả lớp)
b) Tổng số học sinh điểm 9 hoặc 10 chiếm:
25% + 31,25% = 56,25% (số học sinh cả lớp)
c) Lớp đó có tất cả số học sinh là
18 : 56,25 x 100 = 32 (học sinh)
d) Lớp đó có số học sinh không đạt điểm 9 hoặc 10 là:
32 – 18 = 14 (học sinh)
Đáp số: a) 31,25%
b) 56,25%
c) 32 học sinh
d) 14 học sinh
Bài 3. Cho hình thang ABCD có đáy bé AB bằng $\frac{1}{3}$ đáy lớn. Chiều cao bằng 12,6m và bằng hiệu độ dài hai đáy.
a) Tính diện tích hình thang ABCD.
b) Hai đường chéo AC và BD cắt nhau tại O. So sánh SOBC và SOAD.
c) Kéo dài cạnh DA và CB cắt nhau tại P. Tính tỉ số diện tích của hai tam giác DBP và DPC.
Cách giải
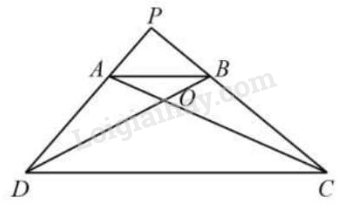
a) Độ dài đáy bé AB là: 12,6 : (3 – 1) x 1 = 6,3 (m)
Độ dài đáy lớn CD là: 6,3 x 3 = 18,9 (m)
Diện tích hình thang ABCD là: (6,3 + 18,9) x 12,6 : 2 = 158,76 (m2)
b) Ta có SDAB = SCAB (Hai tam giác có chung đáy AB và chiều cao bằng nhau)
Mà SDAB = SOAD + SOAB
SCAB = SOBC + SOAB
Nên SOBC = SOAD.
c) Xét tam giác ABD và tam giác ACD có chiều cao hạ từ D xuống AB bằng chiều cao hạ từ B xuống CD nên $\frac{{{S_{ABD}}}}{{{S_{ACD}}}} = \frac{{AB}}{{CD}} = \frac{1}{3}$
Mà tam giác ABD và tam giác ACD lại có chung đáy AD nên chiều cao hạ từ B xuống AD bằng $\frac{1}{3}$ chiều cao hạ từ C xuống AD.
$ \Rightarrow \frac{{{S_{ABP}}}}{{{S_{APC}}}} = \frac{1}{3}$
Mà tam giác ABP và tam giác APC lại chung chiều cao hạ từ A xuống BC nên $\frac{{PB}}{{PC}} = \frac{1}{3}$
Vậy $\frac{{{S_{DBP}}}}{{{S_{DPC}}}} = \frac{{PB}}{{PC}} = \frac{1}{3}$ (hai tam giác chung chiều cao hạ từ D xuống PC)$$
Các bài khác cùng chuyên mục
- Đề thi thử vào lớp 6 môn Toán trường chuyên Ngoại ngữ (đề số 7)
- Đề thi thử vào lớp 6 môn Toán trường chuyên Ngoại ngữ (đề số 6)
- Đề thi thử vào lớp 6 môn Toán trường chuyên Ngoại ngữ (đề số 5)
- Đề minh hoạ thi vào lớp 6 trường THCS và THPT Lương Thế Vinh năm học 2020 - 2021 (đề 3)
- Đề thi vào lớp 6 trường THCS Chu Văn An - Long Biên năm học 2022 - 2023
- Đề thi thử vào lớp 6 môn Toán trường chuyên Ngoại ngữ (đề số 7)
- Đề thi thử vào lớp 6 môn Toán trường chuyên Ngoại ngữ (đề số 6)
- Đề thi thử vào lớp 6 môn Toán trường chuyên Ngoại ngữ (đề số 5)
- Đề minh hoạ thi vào lớp 6 trường THCS và THPT Lương Thế Vinh năm học 2020 - 2021 (đề 3)
- Đề thi vào lớp 6 trường THCS Chu Văn An - Long Biên năm học 2022 - 2023




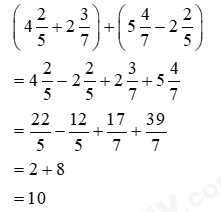









Danh sách bình luận