Đề tham khảo môn Toán kì thi học bổng Ngôi Sao Hà Nội (đề 1)

STT

ĐỀ BÀI

TRẢ LỜI

1

Tìm \(\overline {a,b} \) biết $\overline {a,b}  = (a + b) \times 0,5$

2

Bây giờ là 3 giờ đúng. Tính thời gian gần nhất để hai kim đồng hồ trùng khít lên nhau.

3

Hãy viết phép cộng có tổng bằng 1000 từ các chữ số 8 sao cho số chữ số 8 được sử dụng ít nhất.

4

Tính : 23 phút 5 giây : 5 + 3 phút 31 giây = ....

5

Tìm y, biết y : 8 + y x 8 – 125,888 = 69,112

6

Một đơn vị bộ đội chuẩn bị đủ gạo cho 70 người ăn trong 30 ngày. Sau khi ăn được 6 ngày thì có 10 người chuyển đi nơi khác. Hỏi số gạo còn lại đủ cho đơn vị đó ăn trong bao nhiêu ngày nữa? (Biết rằng mức ăn của mọi người như nhau).

7

Một lớp học chưa đến 50 học sinh. Trong đó 1/10 số học sinh được xếp loại trung bình, 1/8 số học sinh được xếp loại khá còn lại là loại

giỏi. Tính số học sinh giỏi của lớp đó.

8

Tính A, biết $A = \frac{{19,8:0,2 \times 44,44 \times 2 \times 13,2:0,25}}{{3,3 \times 88,88:0,5 \times 6,6:0,125 \times 5}}$

9

Cùng một lúc An đi từ A đến B và Bình đi từ B đến A lúc hai người gặp nhau An đi được 12km. Sau khi gặp nhau An tiếp tục đi đến B rồi quay lại, Bình tiếp tục đi đến A rồi quay lại và họ gặp nhau lần thứ hai cách B 5km. Tính độ dài quãng đường AB.

10

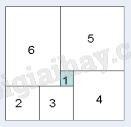
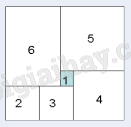
Một tờ bìa hình vuông được chia thành 5 hình vuông và 1 hình chữ nhật (như hình vẽ). Biết hình vuông được tô màu có diện tích 4cm². Tính diện tích tờ bìa ban đầu.

STT

ĐỀ BÀI

TRẢ LỜI

1

Tìm \(\overline {a,b} \) biết $\overline {a,b}  = (a + b) \times 0,5$

Cách giải:

$\overline {a,b}  = (a + b) \times 0,5$

$\overline {ab}  = (a + b) \times 5$ (nhân cả hai vế với 10)

$a \times 10 + b = a \times 5 + b \times 5$

$a \times 5 = b \times 4$

Vậy a = 4, b = 5

4,5

2

Bây giờ là 3 giờ đúng. Tính thời gian gần nhất để hai kim đồng hồ trùng khít lên nhau.

Cách giải:

Lúc 3 giờ kim giờ chỉ số 3, kim phút chỉ số 12.

Hai kim này cách nhau 3 khoảng trên đồng hồ.

Trong 1 giờ kim phút đi được 12 khoảng.

Trong 1 giờ kim giờ đi được 1 khoảng.

Thời gian gần nhất để hai kim đồng hồ trùng khít lên nhau là 3 : (12 – 1) = $\frac{3}{{11}}$ (giờ)

$\frac{3}{{11}}$ giờ

3

Hãy viết phép cộng có tổng bằng 1000 từ các chữ số 8 sao cho số chữ số 8 được sử dụng ít nhất.

Cách giải:

1000 = 888 + 112

1000 = 888 + 88 + 24

1000 = 888 + 88 + 8 + 8 + 8

1000 = 888 + 88 + 8 + 8 + 8

4

Tính: 23 phút 5 giây : 5 + 3 phút 31 giây = ....

Cách giải:

23 phút 5 giây : 5 + 3 phút 31 giây

= 4 phút 37 giây + 3 phút 31 giây

= 8 phút 8 giây

8 phút 8 giây

5

Tìm y, biết y : 8 + y x 8 – 125,888 = 69,112

Cách giải:

y x ($\frac{1}{8}$ + 8) - 125,888 = 69,112

y x $\frac{{65}}{8}$ = 195

y = 195 : $\frac{{65}}{8}$

y = 24

y = 24

6

Một đơn vị bộ đội chuẩn bị đủ gạo cho 70 người ăn trong 30 ngày. Sau khi ăn được 6 ngày thì có 10 người chuyển đi nơi khác. Hỏi số gạo còn lại đủ cho đơn vị đó ăn trong bao nhiêu ngày nữa? (Biết rằng mức ăn của mọi người như nhau).

Cách giải:

Sau 6 ngày, số gạo còn lại đủ cho 70 người ăn trong 24 ngày.

Sau khi 10 người chuyển đi, số gạo còn lại đủ cho đơn vị đó ăn trong só ngày là:

70 x 24 : 60 = 28 (ngày)

28 ngày

7

Một lớp học chưa đến 50 học sinh. Trong đó $\frac{1}{{10}}$ số học sinh được xếp loại trung bình, $\frac{1}{8}$ số học sinh được xếp loại khá còn lại là loại giỏi. Tính số học sinh giỏi của lớp đó.

Cách giải:

Số học sinh của lớp đó cho hết cho 10 và 8 nên số học sinh có thể là 40, 80, 120, …

Vì lớp học chưa đến 50 học sinh nên lớp đó có 40 học sinh.

Số học sinh trung bình là $40 \times \frac{1}{{10}} = 4$ (học sinh)

Số học sinh khá là $40 \times \frac{1}{8} = 5$ (học sinh)

Số học sinh giỏi là: 40 – (4 + 5) = 31 (học sinh)

31 học sinh

8

Tính A, biết $A = \frac{{19,8:0,2 \times 44,44 \times 2 \times 13,2:0,25}}{{3,3 \times 88,88:0,5 \times 6,6:0,125 \times 5}}$

Cách giải:

$A = \frac{{19,8:0,2 \times 44,44 \times 2 \times 13,2:0,25}}{{3,3 \times 88,88:0,5 \times 6,6:0,125 \times 5}}$

$A = \frac{{19,8 \times 5 \times 44,44 \times 2 \times 13,2 \times 4}}{{3,3 \times 88,88 \times 2 \times 6,6 \times 8 \times 5}}$

$A = \frac{{19,8}}{{3,3 \times 2}}$

$A = 3$

$A = 3$

9

Cùng một lúc An đi từ A đến B và Bình đi từ B đến A lúc hai người gặp nhau An đi được 12km. Sau khi gặp nhau An tiếp tục đi đến B rồi quay lại, Bình tiếp tục đi đến A rồi quay lại và họ gặp nhau lần thứ hai cách B 5km. Tính độ dài quãng đường AB.

Cách giải:

Lần gặp thứ nhất: An đi quãng đường AC, Bình đi quãng đường BC

Lần gặp thứ hai: An đi quãng đường AB + BD, Bình đi quãng đường BA + AD

Tổng quãng đường 2 bạn đi là AB + BD + BA + AD = 3 x AB

Tổng quãng đường gấp 3 nên ta có:

AB + BD = AC x 3

AB + 5 = 12 x 3

Vậy AB = 31 (km)

31 km

10

Một tờ bìa hình vuông được chia thành 5 hình vuông và 1 hình chữ nhật (như hình vẽ). Biết hình vuông được tô màu có diện tích 4cm². Tính diện tích tờ bìa ban đầu.

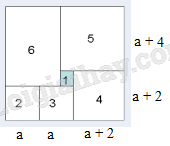
Cách giải:

Hình vuông được tô màu có diện tích 4cm² nên cạnh của hình vuông số 1 là 2 cm.

Ta có a + a + a + 2 = a + 2 + a + 4

3 x a + 2 = 2 x a + 6

a = 4 (cm)

Cạnh của hình vuông lớn là a + a + a + 2 = 4 + 4 + 4 + 2 = 14 (cm)

Diện tích hình vuông là: 14 x 14 = 196 (cm²)

196 cm²