Đề thi vào lớp 6 môn Toán trường Nam Từ Liêm năm 2025

Đề bài

ĐỀ ĐÁNH GIÁ NĂNG LỰC TUYỂN SINH LỚP 6 TRƯỜNG THCS NAM TỪ LIÊM

NĂM HỌC 2025 – 2026

Thời gian làm bài: 45 phút

PHẦN A. TRẮC NGHIỆM

Câu 1. Kết quả của phép tính: $\frac{2}{7} + \frac{6}{{13}} + \frac{{12}}{7} + \frac{7}{{13}}$

Câu 2. Tìm $x$ biết: $x \times 4,9 + x \times 5,1 = 30$

Câu 3. Một người cầm 100 000 đồng mua 4 bút bi và 7 quyển vở. Biết giá một cái bút bi là 4 500 đồng, giá một quyển vở là 7 000 đồng. Hỏi người đó còn lại bao nhiêu tiền?

Câu 4. Gieo 10 lần con xúc xắc, kết quả nhận được là 3 lần mặt ngửa. Tỉ số của số lần nhận được mặt úp so với tổng số lần gieo?

Câu 5. Một người gửi vào ngân hàng 20 triệu đồng với lãi suất là 6% một năm. Hỏi sau một năm số tiền lãi nhận được là bao nhiêu?

Câu 6. Một bể nước hình hộp chữ nhật có chiều dài 80cm, chiều rộng 40cm, chiều cao 60cm. Hỏi bể nước chứa được bao nhiêu lít nước?

Câu 7. Nam đi từ nhà lúc 7 giờ và đến trường lúc 7 giờ 15 phút. Biết vận tốc của Nam là 10km/giờ. Tính quãng đường từ nhà Nam đến trường?

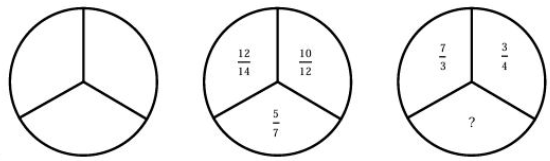
Câu 8. Tìm phân số thích hợp thay cho dấu ?

Câu 9. Câu lạc bộ thể thao có 60 học sinh. Các môn được mô tả theo biểu đồ hình bên.

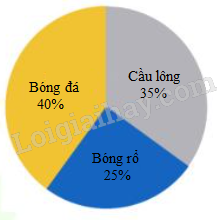
Quan sát hình và trả lời các câu hỏi sau bằng cách trả lời Đúng - Sai.

a) Bóng đá là môn thể thao có nhiều học sinh tham gia nhất.

b) Câu lạc bộ bóng rổ có 12 học sinh.

c) Số học sinh tham gia môn cầu lông gấp đôi số học sinh tham gia môn bóng đá.

d) Số học sinh tham gia môn cầu lông nhiều hơn số học sinh tham gia môn bóng đá là 6 học sinh.

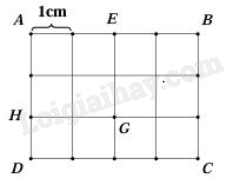
Câu 10. Cho hình vuông ABCD được tạo bởi các hình vuông cạnh 1 cm như hình vẽ.

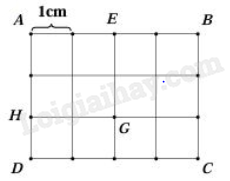
Quan sát hình và trả lời các câu hỏi sau bằng cách trả lời Đúng - Sai.

a) Chu vi hình vuông AEGH là 4 cm.

b) Diện tích hình vuông AEGH là 4 cm².

c) S_AEGH = $\frac{1}{3}$ x S_ABCD

d) Tổng số hình vuông là 18 hình.

PHẦN B. TỰ LUẬN

Câu 1. Một cửa hàng nhập về 2000 vật phẩm gồm mũ, áo, nón nhân dịp 30/4 - 1/5. Biết số áo bằng $\frac{2}{5}$ tổng.

a) Một chiếc áo bán ra lãi 30 000 đồng. Hỏi khi bán hết áo thì số tiền lãi nhận được là bao nhiêu?

b) Nếu nhập thêm 100 mũ, giảm 50 nón thì số mũ bằng số nón. Tính số mũ, nón ban đầu.

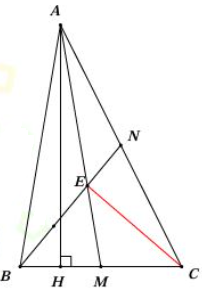
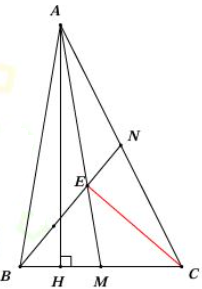
Câu 2. Cho tam giác ABC, AN = NC, BE = $\frac{2}{3}$ BN, AE kéo dài cắt BC tại M. Biết S_ABN = 6 cm².

a) Tính S_ABE.

b) Biết BC = 4cm, tính độ dài đường cao hạ từ A xuống đáy BC.

c) Tính độ dài BM.

Câu 3. Ba bạn vào chung một cửa hàng, Việt mua 4 hộp sữa, 1 chai nước và 10 cái bánh ngọt hết 87 000 đồng. Bảo mua 3 hộp sữa, 1 chai nước và 7 cái bánh ngọt hết 64 000 đồng. Vậy Mai mua mỗi loại một cái thì hết bao nhiêu tiền?

Đáp án

HƯỚNG DẪN GIẢI CHI TIẾT

PHẦN A. TRẮC NGHIỆM

Câu 1. Kết quả của phép tính: $\frac{2}{7} + \frac{6}{{13}} + \frac{{12}}{7} + \frac{7}{{13}}$

Cách giải:

$\frac{2}{7} + \frac{6}{{13}} + \frac{{12}}{7} + \frac{7}{{13}} = \left( {\frac{2}{7} + \frac{{12}}{7}} \right) + \left( {\frac{6}{{13}} + \frac{7}{{13}}} \right) = \frac{{14}}{7} + \frac{{13}}{{13}} = 2 + 1 = 3$

Đáp số: 3

Câu 2. Tìm $x$ biết: $x \times 4,9 + x \times 5,1 = 30$

Cách giải:

$x \times 4,9 + x \times 5,1 = 30$

$x \times \left( {4,9 + 5,1} \right) = 30$

$x \times 10 = 30$

$x = 30:10$

$x = 3$

Đáp số: x = 3

Câu 3. Một người cầm 100 000 đồng mua 4 bút bi và 7 quyển vở. Biết giá một cái bút bi là 4 500 đồng, giá một quyển vở là 7 000 đồng. Hỏi người đó còn lại bao nhiêu tiền?

Cách giải:

Giá tiền 4 cái bút bi là: 4 500 × 4 = 18 000 (đồng)

Giá tiền 7 quyển vở là: 7 000 × 7 = 49 000 (đồng)

Tổng số tiền người đó phải trả là: 18 000 + 49 000 = 67 000 (đồng)

Người đó còn lại số tiền là: 100 000 – 67 000 = 33 000 (đồng)

Đáp số: 33 000 đồng

Câu 4. Gieo 10 lần con xúc xắc, kết quả nhận được là 3 lần mặt ngửa. Tỉ số của số lần nhận được mặt úp so với tổng số lần gieo?

Cách giải:

Số lần xuất hiện mặt úp là: 10 - 3 = 7 (lần)

Tỉ số lần xuất hiện mặt úp so với tổng số lần gieo là $\frac{7}{{10}}$

Đáp số: $\frac{7}{{10}}$

Câu 5. Một người gửi vào ngân hàng 20 triệu đồng với lãi suất là 6% một năm. Hỏi sau một năm số tiền lãi nhận được là bao nhiêu?

Cách giải:

Số tiền lãi nhận được sau 1 năm là:

20 000 000 × 6% = 1 200 000 (đồng)

Đáp số: 1 200 000 đồng

Câu 6. Một bể nước hình hộp chữ nhật có chiều dài 80cm, chiều rộng 40cm, chiều cao 60cm. Hỏi bể nước chứa được bao nhiêu lít nước?

Cách giải:

Thể tích của bể nước là: 80 × 40 × 60 = 192 000 cm³ = 192 dm³ = 192 lít

Đáp số: 192 lít

Câu 7. Nam đi từ nhà lúc 7 giờ và đến trường lúc 7 giờ 15 phút. Biết vận tốc của Nam là 10km/giờ. Tính quãng đường từ nhà Nam đến trường?

Cách giải:

Thời gian Nam đi từ nhà đến trưởng là: 7 giờ 15 phút – 7 giờ = 15 phút = 0,25 giờ

Quãng đường từ nhà trường là: 10 × 0,25 = 2,5 (km)

Đáp số: 2,5 km

Câu 8. Tìm phân số thích hợp thay cho dấu ?

Cách giải:

Hình 2: $\frac{{12}}{{14}} \times \frac{{10}}{{12}} = \frac{5}{7}$

Hình 3: $\frac{7}{3} \times \frac{3}{4} = \frac{7}{4}$

Đáp số: $\frac{7}{4}$

Câu 9. Câu lạc bộ thể thao có 60 học sinh. Các môn được mô tả theo biểu đồ hình bên.

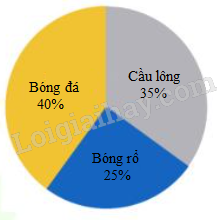
Quan sát hình và trả lời các câu hỏi sau bằng cách trả lời Đúng - Sai.

a) Bóng đá là môn thể thao có nhiều học sinh tham gia nhất.

b) Câu lạc bộ bóng rổ có 12 học sinh.

c) Số học sinh tham gia môn cầu lông gấp đôi số học sinh tham gia môn bóng đá.

d) Số học sinh tham gia môn cầu lông nhiều hơn số học sinh tham gia môn bóng đá là 6 học sinh.

Cách giải:

a) Vì 40% > 35% > 25% nên bóng đá có nhiều người tham gia nhất.

Vậy đáp án Đúng.

b) Số học sinh tham gia bóng rổ là: 60 × 25% = 1560 × 25% = 15 (học sinh)

Vậy đáp án Sai.

c) Số học sinh tham gia cầu lông là: 60 × 35% = 2160 × 35% = 21 (học sinh)

Số học sinh tham gia bóng đá là: 60 × 40% = 2460 × 40% = 24 (học sinh)

Tỉ số của số học sinh tham gia môn cầu lông và số học sinh tham gia môn bóng đá là 21 : 24 = $\frac{7}{8}$

Vậy đáp án Sai.

d) Số học sinh tham gia cầu lông hơn số học sinh tham gia bóng rổ là: 21 – 15 = 6 (học sinh)

Vậy đáp án Đúng.

Câu 10. Cho hình vuông ABCD được tạo bởi các hình vuông cạnh 1 cm như hình vẽ.

Quan sát hình và trả lời các câu hỏi sau bằng cách trả lời Đúng - Sai.

a) Chu vi hình vuông AEGH là 4 cm.

b) Diện tích hình vuông AEGH là 4 cm².

c) S_AEGH = $\frac{1}{3}$ x S_ABCD

d) Tổng số hình vuông là 18 hình.

Cách giải:

a. Chu vi hình vuông AEGH là: 2 × 4 = 8 (cm)

Vậy câu a sai.

b. Diện tích hình vuông AEGH là: 2 × 2 = 4 (cm²)

Vậy câu b đúng.

c. Chiều dài hình chữ nhật ABCD là: 1 × 4 = 4 cm

Chiều rộng hình chữ nhật ABCD là: 1 × 3 = 3 cm

Diện tích hình chữ nhật ABCD là: 4 x 3 = 12 (cm²)

Vậy tỉ số diện tích hình AEGH và ABCD là: $\frac{4}{{12}} = \frac{1}{3}$

Vậy câu c đúng.

d. Số hình vuông 1 × 1 là: 12 (hình)

Số hình vuông 2 × 2 là: 6 (hình)

Số hình vuông 3 × 3 là: 2 (hình)

Vậy tổng cộng có: 12 + 6 + 2 = 20 hình

Vậy câu d sai.

PHẦN B. TỰ LUẬN

Câu 1. Một cửa hàng nhập về 2000 vật phẩm gồm mũ, áo, nón nhân dịp 30/4 - 1/5. Biết số áo bằng $\frac{2}{5}$ tổng.

a) Một chiếc áo bán ra lãi 30 000 đồng. Hỏi khi bán hết áo thì số tiền lãi nhận được là bao nhiêu?

b) Nếu nhập thêm 100 mũ, giảm 50 nón thì số mũ bằng số nón. Tính số mũ, nón ban đầu.

Cách giải:

a) Số áo nhập về là: $2000 \times \frac{2}{5} = 800$ (cái)

Số tiền lãi nhận được khi bán hết áo là: 30 000 x 800 = 24 000 000 (đồng)

b) Tổng số mũ và nón là: 2000 – 800 = 1 200 (cái)

Tổng số mũ và nón lúc sau là: 1200 + 100 – 50 = 1250 (cái)

Lúc sau số mũ và nón mỗi loại là: 1250 : 2 = 625 (cái)

Số mũ ban đầu là: 625 – 100 = 525 (cái)

Số nón ban đầu là: 625 + 50 = 675 (cái)

Đáp số: a) 24 000 000 đồng

            b) mũ: 525 cái, nón: 675 cái

Câu 2. Cho tam giác ABC, AN = NC, BE = $\frac{2}{3}$ BN, AE kéo dài cắt BC tại M. Biết S_ABN = 6 cm².

a) Tính S_ABE.

b) Biết BC = 4cm, tính độ dài đường cao hạ từ A xuống đáy BC.

c) Tính độ dài BM.

Cách giải:

a) S_ABE = $\frac{2}{3}$S_ABN (Chung chiều cao hạ từ A và đáy BE = $\frac{2}{3}$ BN)

Suy ra S_ABE = $\frac{2}{3} \times 6 = 4$ (cm²)

b) Kẻ AH vuông góc với BC thì AH là đường cao hạ từ đỉnh A xuống đáy BC.

S_ABN = $\frac{1}{2}$ S_ABC (Chung chiều cao hạ từ đỉnh B và đáy AN = $\frac{1}{2}$AC)

Suy ra S_ABC = 2 x S_ABN = 2 x 6 = 12 (cm²)

Mà S_ABC = $\frac{1}{2} \times AH \times BC$ nên AH = 2 x S_ABC : BC = 2 x 12 : 4 = 6 (cm)

c) Nối E với C

Ta có S_ABE = 2 S_AEN (Chung chiều cao hạ từ đỉnh A và đáy BE = 2 EN)

Ta có S_AEC = 2 S_AEN (Chung chiều cao hạ từ đỉnh E và đáy AC = 2 AN)

Suy ra S_ABE = S_AEC. Mà hai tam giác này chung đáy AE.

Suy ra đường cao hạ từ B bằng đường cao hạ từ C xuống đáy AE.

Đưa hai đường cao này vào tam giác ABM và ACM, ta được:

S_АВМ = S_ACM (chung đáy AM, đường cao hạ từ B xuống AM bằng đường cao hạ từ C  xuống AM)

Mặt khác, hai tam giác này lại chung đường cao hạ từ đỉnh A nên đáy BM = MC

Vậy độ dài đoạn BM = BC : 2 = 4 : 2 = 2 (cm)

Đáp số: a) 4 cm²

              b) 6cm

              c) 2cm

Câu 3. Ba bạn vào chung một cửa hàng, Việt mua 4 hộp sữa, 1 chai nước và 10 cái bánh ngọt hết 87000 đồng. Bảo mua 3 hộp sữa, 1 chai nước và 7 cái bánh ngọt hết 64 000 đồng. Vậy Mai mua mỗi loại một cái thì hết bao nhiêu tiền?

Cách giải:

4 hộp sữa + 1 chai nước + 10 bánh ngọt = 87000 (đồng)

3 hộp sữa + 1 chai nước + 7 bánh ngọt = 64000 (đồng)

Giá tiền của 1 hộp sữa và 3 cái bánh ngọt là: 87000 – 64000 = 23000 (đồng)

Giá tiền của 2 hộp sữa và 6 cái bánh ngọt là: 23000 × 2 = 46000 (đồng)

Giá tiền của 1 hộp sữa, 1 chai nước và 1 cái bánh ngọt là: 64000 – 46000 = 18000 (đồng)

Đáp số: 18 000 đồng