-
Đề kiểm tra 15 phút
-
Đề kiểm tra 15 phút - Chương I - Giải Tích 12
-
Đề kiểm tra 15 phút - Chương II - Giải Tích 12
-
Đề kiểm tra 15 phút - Chương III - Giải Tích 12
-
Đề kiểm tra 15 phút – Chương IV – Giải tích 12
-
Đề kiểm tra 15 phút - Chương I - Hình học 12
-
Đề kiểm tra 15 phút - Chương II - Hình học 12
-
Đề kiểm tra 15 phút - Chương III - Hình học 12
-
-
Đề kiểm tra 1 tiết
-
Đề kiểm tra 45 phút (1 tiết) - Chương I - Giải Tích 12
-
Đề kiểm tra 45 phút (1 tiết) - Chương II - Giải Tích 12
-
Đề kiểm tra 45 phút (1 tiết) - Chương III - Giải Tích 12
-
Đề kiểm tra 45 phút (1 tiết) - Chương IV - Giải Tích 12
-
Đề kiểm tra 45 phút (1 tiết) - Chương I - Hình học 12
-
Đề kiểm tra 45 phút (1 tiết) - Chương II - Hình học 12
-
Đề kiểm tra 45 phút (1 tiết) - Chương III - Hình học 12
-
-
Đề thi giữa học kì 1
-
Đề thi học kì 1
-
Đề thi giữa học kì 2
-
Đề thi học kì 2
-
ĐỀ THI THỬ THPT QUỐC GIA MÔN TOÁN
Đề thi THPT QG chính thức - 2021 lần 1 - mã đề 104
Đề bài
Đề thi THPT QG – 2021 lần 1– mã 104
Cho hai số phức \(z = 3 + 2i\) và \({\rm{w}} = 1 - 4i\). Số phức \(z + {\rm{w}}\) bằng
-
A.
\(4 + 2i\)
-
B.
\(4 - 2i\)
-
C.
\( - 2 - 6i\)
-
D.
\(2 + 6i\)
Đề thi THPT QG – 2021 lần 1– mã 104
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên?
-
A.
\(y = {x^3} - 3x + 1\)
-
B.
\(y = {x^4} + 4{x^2} + 1\)
-
C.
\(y = - {x^3} + 3x + 1\)
-
D.
\(y = - {x^4} + 2{x^2} + 1\)
Đề thi THPT QG – 2021 lần 1– mã 104
Nếu \(\int\limits_1^4 {f\left( x \right)dx = 4} \) và \(\int\limits_1^4 {g\left( x \right)dx = - 3} \) thì \(\int\limits_1^4 {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} \) bằng
-
A.
\(1\)
-
B.
\( - 7\)
-
C.
\( - 1\)
-
D.
\(7\)
Đề thi THPT QG – 2021 lần 1– mã 104
Tiệm cận đứng của đồ thị hàm số \(y = \dfrac{{x - 1}}{{x + 2}}\) là đường thẳng có phương trình:\(\)-
A.
\(x = 2\)
-
B.
\(x = - 1\)
-
C.
\(x = - 2\)
-
D.
\(x = 1\)
Đề thi THPT QG – 2021 lần 1– mã 104
Trong không gian \(Oxyz,\) cho mặt cầu \(\left( S \right)\) có tâm \(I\left( { - 1;3;0} \right)\) và bán kính bằng \(2.\) Phương trình của \(\left( S \right)\) là:
-
A.
\({\left( {x - 1} \right)^2} + {\left( {y + 3} \right)^2} + {z^2} = 2\)
-
B.
\({\left( {x - 1} \right)^2} + {\left( {y + 3} \right)^2} + {z^2} = 4\)
-
C.
\({\left( {x + 1} \right)^2} + {\left( {y - 3} \right)^2} + {z^2} = 4\)
-
D.
\({\left( {x + 1} \right)^2} + {\left( {y - 3} \right)^2} + {z^2} = 2\)
-
A.
\(\left( { - \infty ;{{\log }_2}5} \right)\)
-
B.
\(\left( {{{\log }_5}2; + \infty } \right)\)
-
C.
\(\left( { - \infty ;{{\log }_5}2} \right)\)
-
D.
\(\left( {{{\log }_2}5; + \infty } \right)\)
Đề thi THPT QG – 2021 lần 1– mã 104
Thể tích của khối lập phương cạnh \(2a\) bằng:
-
A.
\({a^3}\)
-
B.
\(2{a^3}\)
-
C.
\(8{a^3}\)
-
D.
\(4{a^3}\)
Đề thi THPT QG – 2021 lần 1– mã 104
Trên khoảng \(\left( {0; + \infty } \right),\) đạo hàm của hàm số \(y = {x^{\frac{5}{3}}}\) là:
-
A.
\(y' = \dfrac{3}{8}{x^{\frac{8}{3}}}\)
-
B.
\(y' = \dfrac{5}{3}{x^{\frac{2}{3}}}\)
-
C.
\(y' = \dfrac{5}{3}{x^{ - \frac{2}{3}}}\)
-
D.
\(y' = \dfrac{3}{5}{x^{\frac{2}{3}}}\)
Đề thi THPT QG – 2021 lần 1– mã 104
Trong không gian \(Oxyz,\) cho điểm \(A\left( {2; - 1;4} \right)\). Tọa độ của vectơ \(\overrightarrow {OA} \) là
-
A.
\(\left( { - 2;1;4} \right)\)
-
B.
\(\left( {2; - 1;4} \right)\)
-
C.
\(\left( {2;1;4} \right)\)
-
D.
\(\left( { - 2;1; - 4} \right)\)
Đề thi THPT QG – 2021 lần 1– mã 104
Nếu \(\int\limits_0^3 {f\left( x \right)dx = 3} \) thì \(\int\limits_0^3 {4f\left( x \right)dx} \) bằng
-
A.
\(3\)
-
B.
\(12\)
-
C.
\(36\)
-
D.
\(4\)
Đề thi THPT QG – 2021 lần 1– mã 104
Cho cấp số nhân \(\left( {{u_n}} \right)\) với \({u_1} = 2\) và \({u_2} = 10\). Công bội của cấp số nhân đã cho bằng
-
A.
\( - 8\)
-
B.
\(8\)
-
C.
\(5\)
-
D.
\(\dfrac{1}{5}\)
Đề thi THPT QG – 2021 lần 1– mã 104
Với \(n\) là số nguyên dương bất kì, \(n \ge 3,\) công thức nào dưới đây đúng?
-
A.
\(A_n^3 = \dfrac{{\left( {n - 3} \right)!}}{{n!}}\)
-
B.
\(A_n^3 = \dfrac{{3!}}{{\left( {n - 3} \right)!}}\)
-
C.
\(A_n^3 = \dfrac{{n!}}{{\left( {n - 3} \right)!}}\)
-
D.
\(A_n^3 = \dfrac{{n!}}{{3!\left( {n - 3} \right)!}}\)
Đề thi THPT QG – 2021 lần 1– mã 104
Cho hàm số \(f\left( x \right) = {x^2} + 2.\) Khẳng định nào dưới đây đúng?
-
A.
\(\int {f\left( x \right)dx = 2x + C} \)
-
B.
\(\int {f\left( x \right)dx = \dfrac{{{x^3}}}{3} + 2x + C} \)
-
C.
\(\int {f\left( x \right)dx = {x^2} + 2x + C} \)
-
D.
\(\int {f\left( x \right)dx = {x^3} + 2x + C} \)
Đề thi THPT QG – 2021 lần 1– mã 104
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng
-
A.
\(0\)
-
B.
\(3\)
-
C.
\(1\)
-
D.
\( - 1\)
Đề thi THPT QG – 2021 lần 1– mã 104
Trong không gian \(Oxyz,\) cho mặt phẳng \(\left( P \right):2x + 4y - z - 1 = 0.\) Vectơ nào dưới đây là một vectơ pháp tuyến của \(\left( P \right)?\)
-
A.
\(\overrightarrow {{n_2}} = \left( {2; - 4;1} \right)\)
-
B.
\(\overrightarrow {{n_1}} = \left( {2;4;1} \right)\)
-
C.
\(\overrightarrow {{n_3}} = \left( {2;4; - 1} \right)\)
-
D.
\(\overrightarrow {{n_4}} = \left( { - 2;4;1} \right)\)
-
A.
\(2\)
-
B.
\( - 4\)
-
C.
\(4\)
-
D.
\( - 2\)
Đề thi THPT QG – 2021 lần 1– mã 104
Nghiệm của phương trình \({\log _2}\left( {5x} \right) = 3\) là
-
A.
\(x = \dfrac{8}{5}\)
-
B.
\(x = \dfrac{9}{5}\)
-
C.
\(x = 8\)
-
D.
\(x = 9\)
-
A.
\(\mathbb{R}\backslash \left\{ 0 \right\}\)
-
B.
\(\mathbb{R}\)
-
C.
\(\left[ {0; + \infty } \right)\)
-
D.
\(\left( {0; + \infty } \right)\)
Đề thi THPT QG – 2021 lần 1– mã 104
Cho \(a > 0\) và \(a \ne 1,\) khi đó \({\log _a}\sqrt[5]{a}\) bằng
-
A.
\(\dfrac{1}{5}\)
-
B.
\( - \dfrac{1}{5}\)
-
C.
\(5\)
-
D.
\( - 5\)
Đề thi THPT QG – 2021 lần 1– mã 104
Trong không gian \(Oxyz,\) cho đường thẳng \(d\) đi qua điểm \(M\left( {1;5; - 2} \right)\) và có một vectơ chỉ phương \(\overrightarrow u = \left( {3; - 6;1} \right).\) Phương trình của \(d\) là:
-
A.
\(\left\{ \begin{array}{l}x = 3 + t\\y = - 6 + 5t\\z = 1 - 2t\end{array} \right.\)
-
B.
\(\left\{ \begin{array}{l}x = 1 + 3t\\y = 5 - 6t\\z = 2 + t\end{array} \right.\)
-
C.
\(\left\{ \begin{array}{l}x = 1 + 3t\\y = 5 + 6t\\z = - 2 + t\end{array} \right.\)
-
D.
\(\left\{ \begin{array}{l}x = 1 + 3t\\y = 5 - 6t\\z = - 2 + t\end{array} \right.\)
Đề thi THPT QG – 2021 lần 1– mã 104
Trên mặt phẳng tọa độ, điểm \(M\left( { - 4;3} \right)\) là điểm biểu diễn của số phức nào dưới đây?
-
A.
\({z_3} = - 4 - 3i\)
-
B.
\({z_4} = 4 + 3i\)
-
C.
\({z_2} = 4 - 3i\)
-
D.
\({z_1} = - 4 + 3i\)
Đề thi THPT QG – 2021 lần 1– mã 104
Cho hàm số \(f\left( x \right)\) có bảng xét dấu của đạo hàm như sau:
Số điểm cực trị của hàm số đã cho là
-
A.
\(3\)
-
B.
\(4\)
-
C.
\(2\)
-
D.
\(5\)
Đề thi THPT QG – 2021 lần 1– mã 104
Cho hàm số \(f\left( x \right) = {e^x} + 4\). Khẳng định nào dưới đây đúng?
-
A.
\(\int {f\left( x \right)dx = {e^x} + 4x + C.} \)
-
B.
\(\int {f\left( x \right)dx = {e^x} + C.} \)
-
C.
\(\int {f\left( x \right)dx = {e^{x - 4}} + C.} \)
-
D.
\(\int {f\left( x \right)dx = {e^x} - 4x + C.} \)
Đề thi THPT QG – 2021 lần 1– mã 104
Cho hàm số \(y = f\left( x \right)\) có đồ thị là đường cong trong hình bên. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
-
A.
\(\left( { - 1;1} \right)\)
-
B.
\(\left( {1; + \infty } \right)\)
-
C.
\(\left( { - \infty ;1} \right)\)
-
D.
\(\left( {0;3} \right)\)
Đề thi THPT QG – 2021 lần 1– mã 104
Diện tích \(S\) của mặt cầu bán kính \(R\) được tính theo công thức nào dưới đây?
-
A.
\(S = \pi {R^2}\)
-
B.
\(S = 16\pi {R^2}\)
-
C.
\(S = 4\pi {R^2}\)
-
D.
\(S = \dfrac{4}{3}\pi {R^2}\)
Đề thi THPT QG – 2021 lần 1– mã 104
Đồ thị của hàm số \(y = - 2{x^3} + 3{x^2} - 5\) cắt trục tung tại điểm có tung độ bằng
-
A.
\( - 5\)
-
B.
\(0\)
-
C.
\( - 1\)
-
D.
\(2\)
Đề thi THPT QG – 2021 lần 1– mã 104
Cho khối chóp có diện tích đáy \(B = 8{a^2}\) và chiều cao \(h = a\). Thể tích của khối chóp đã cho bằng
-
A.
\(8{a^3}\)
-
B.
\(\dfrac{4}{3}{a^3}\)
-
C.
\(4{a^3}\)
-
D.
\(\dfrac{8}{3}{a^3}\)
Đề thi THPT QG – 2021 lần 1– mã 104
Cho khối trụ có bán kính đáy \(r = 5\) và chiều cao \(h = 3\). Thể tích của khối trụ đã cho bằng
-
A.
\(15\pi \)
-
B.
\(75\pi \)
-
C.
\(25\pi \)
-
D.
\(45\pi \)
Đề thi THPT QG – 2021 lần 1– mã 104
Trong không gian \(Oxyz,\) cho điểm \(M\left( {2;1; - 2} \right)\) và mặt phẳng \(\left( P \right):3x + 2y - z + 1 = 0\). Đường thẳng đi qua \(M\) và vuông góc với \(\left( P \right)\) có phương trình là:
-
A.
\(\dfrac{{x - 2}}{3} = \dfrac{{y - 1}}{2} = \dfrac{{z + 2}}{{ - 1}}\)
-
B.
\(\dfrac{{x - 2}}{3} = \dfrac{{y - 1}}{2} = \dfrac{{z + 2}}{1}\)
-
C.
\(\dfrac{{x + 2}}{3} = \dfrac{{y + 1}}{2} = \dfrac{{z - 2}}{1}\)
-
D.
\(\dfrac{{x + 2}}{3} = \dfrac{{y + 1}}{2} = \dfrac{{z - 2}}{{ - 1}}\)
Đề thi THPT QG – 2021 lần 1– mã 104
Cho hình lăng trụ đứng \(ABC.A'B'C'\) có tất cả các cạnh bằng nhau (tham khảo hình bên). Góc giữa hai đường thẳng \(AB'\) và \(CC'\) bằng
-
A.
\({30^o}\)
-
B.
\({90^o}\)
-
C.
\({60^o}\)
-
D.
\({45^o}\)
Đề thi THPT QG – 2021 lần 1– mã 104
Cho hình chóp \(S.ABC\) có đáy là tam giác vuông cân tại \(B,\) \(AB = 4a\) và \(SA\) vuông góc với mặt phẳng đáy. Khoảng cách từ \(C\) đến mặt phẳng \(\left( {SAB} \right)\) bằng
-
A.
\(4a\)
-
B.
\(4\sqrt 2 a\)
-
C.
\(2\sqrt 2 a\)
-
D.
\(2a\)
Đề thi THPT QG – 2021 lần 1– mã 104
Nếu \(\int\limits_0^2 {f\left( x \right)dx = 4} \) thì \(\int\limits_0^2 {\left[ {2f\left( x \right) - 1} \right]dx} \) bằng
-
A.
\(8\)
-
B.
\(10\)
-
C.
\(7\)
-
D.
\(6\)
Đề thi THPT QG – 2021 lần 1– mã 104
Biết hàm số \(y = \dfrac{{x + a}}{{x - 1}}\) \((a\) là số thực cho trước, \(a \ne 1)\) có đồ thị như trong hình bên. Mệnh đề nào dưới đây đúng?
-
A.
(y' < 0,\,\forall x \in \mathbb{R}\)
-
B.
\(y' < 0,\,\forall x \ne 1\)
-
C.
\(y' > 0,\,\forall x \in \mathbb{R}\)
-
D.
\(y' > 0,\,\forall x \ne 1\)
Đề thi THPT QG – 2021 lần 1– mã 104
Cho số phức \(z\) thỏa mãn \(iz = 4 + 3i.\) Số phức liên hợp của \(z\) là
-
A.
\(\overline z = 3 + 4i\)
-
B.
\(\overline z = - 3 - 4i\)
-
C.
\(\overline z = 3 - 4i\)
-
D.
\(\overline z = - 3 + 4i\)
Đề thi THPT QG – 2021 lần 1– mã 104
Từ một hộp chứa \(12\) quả bóng gồm \(5\) quả màu đỏ và \(7\) quả màu xanh, lấy ngẫu nhiên đồng thời \(3\) quả. Xác suất để lấy được \(3\) quả màu đỏ bằng
-
A.
\(\dfrac{1}{{22}}\)
-
B.
\(\dfrac{7}{{44}}\)
-
C.
\(\dfrac{5}{{12}}\)
-
D.
\(\dfrac{2}{7}\)
Đề thi THPT QG – 2021 lần 1– mã 104
Với mọi \(a,b\) thỏa mãn \({\log _2}{a^3} + {\log _2}b = 5,\) khẳng định nào dưới đây đúng?
-
A.
\({a^3}b = 32\)
-
B.
\({a^3}b = 25\)
-
C.
\({a^3} + b = 25\)
-
D.
\({a^3} + b = 32\)
Đề thi THPT QG – 2021 lần 1– mã 104
Trên đoạn \(\left[ { - 1;2} \right],\) hàm số \(y = {x^3} + 3{x^2} + 1\) đạt giá trị nhỏ nhất tại điểm
-
A.
\(x = 2\)
-
B.
\(x = 0\)
-
C.
\(x = - 1\)
-
D.
\(x = 1\)
Đề thi THPT QG – 2021 lần 1– mã 104
Trong không gian \(Oxyz,\) cho hai điểm \(A\left( {1;0;0} \right)\) và \(B\left( {3;2;1} \right).\) Mặt phẳng đi qua \(A\) và vuông góc với \(AB\) có phương trình là:
-
A.
\(2x + 2y + z - 2 = 0\)
-
B.
\(4x + 2y + z - 17 = 0\)
-
C.
\(4x + 2y + z - 4 = 0\)
-
D.
\(2x + 2y + z - 11 = 0\)
Đề thi THPT QG – 2021 lần 1– mã 104
Cho hàm số bậc bốn \(y = f\left( x \right)\) có đồ thị là đường cong trong hình trên. Số nghiệm thực phân biệt của phương trình \(f\left( {f\left( x \right)} \right) = 0\) là
-
A.
\(12\)
-
B.
\(10\)
-
C.
\(8\)
-
D.
\(4\)
Đề thi THPT QG – 2021 lần 1– mã 104
Có bao nhiêu số nguyên \(x\) thỏa mãn \(\left( {{2^{{x^2}}} - {4^x}} \right)\left[ {{{\log }_3}\left( {x + 25} \right) - 3} \right] \le 0\)?
-
A.
\(24\)
-
B.
vô số
-
C.
\(25\)
-
D.
\(26\)
Đề thi THPT QG – 2021 lần 1– mã 104
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}2x + 2\,\,\,\,\,khi\,\,x \ge 1\\3{x^2} + 1\,\,\,khi\,\,x < 1\end{array} \right..\) Giả sử \(F\) là nguyên hàm của \(f\) trên \(\mathbb{R}\) thỏa mãn \(F\left( 0 \right) = 2\). Giá trị của \(F\left( { - 1} \right) + 2F\left( 2 \right)\) bằng
-
A.
\(18\)
-
B.
\(20\)
-
C.
\(9\)
-
D.
\(24\)
Đề thi THPT QG – 2021 lần 1– mã 104
Cắt hình nón \(\left( \aleph \right)\) bởi mặt phẳng đi qua đỉnh và tạo với mặt phẳng chứa đáy một góc bằng \({30^o}\), ta được thiết diện là tam giác đều cạnh \(2a.\) Diện tích xung quanh của \(\left( \aleph \right)\) bằng
-
A.
\(\sqrt 7 \pi {a^2}\)
-
B.
\(\sqrt {13} \pi {a^2}\)
-
C.
\(2\sqrt {13} \pi {a^2}\)
-
D.
\(2\sqrt 7 \pi {a^2}\)
Đề thi THPT QG – 2021 lần 1– mã 104
Trong không gian \(Oxyz,\) cho đường thẳng \(d:\dfrac{x}{1} = \dfrac{y}{{ - 1}} = \dfrac{{z - 1}}{2}\) và mặt phẳng \(\left( P \right):x + 2y - 2z + 2 = 0\). Hình chiếu vuông góc của \(d\) trên \(\left( P \right)\) là đường thẳng có phương trình:
-
A.
\(\dfrac{x}{{ - 2}} = \dfrac{y}{4} = \dfrac{{z - 1}}{3}\)
-
B.
\(\dfrac{x}{{14}} = \dfrac{y}{1} = \dfrac{{z + 1}}{8}\)
-
C.
\(\dfrac{x}{{ - 2}} = \dfrac{y}{4} = \dfrac{{z + 1}}{3}\)
-
D.
\(\dfrac{x}{{14}} = \dfrac{y}{1} = \dfrac{{z - 1}}{8}\)
Đề thi THPT QG – 2021 lần 1– mã 104
Có bao nhiêu số nguyên \(y\) sao cho tồn tại \(x \in \left( {\dfrac{1}{3};6} \right)\) thỏa mãn \({27^{3{x^2} + xy}} = \left( {1 + xy} \right){27^{18x}}\)
-
A.
\(19\)
-
B.
\(20\)
-
C.
\(18\)
-
D.
\(21\)
Đề thi THPT QG – 2021 lần 1– mã 104
Trên tập hợp các số phức, xét phương trình \({z^2} - 2\left( {m + 1} \right)z + {m^2} = 0\)\((m\) là tham số thực). Có bao nhiêu giá trị của \(m\) để phương trình đó có nghiệm \({z_0}\) thỏa mãn \(\left| {{z_0}} \right| = 6\)?
-
A.
\(4\)
-
B.
\(1\)
-
C.
\(2\)
-
D.
\(3\)
Đề thi THPT QG – 2021 lần 1– mã 104
Cho khối hộp chữ nhật \(ABCD.A'B'C'D'\) có đáy là hình vuông, \(BD = 4a\), góc giữa hai mặt phẳng \(\left( {A'BD} \right)\) và \(\left( {ABCD} \right)\) bằng \({60^o}\). Thể tích của khối hộp chữ nhật đã cho bằng
-
A.
\(48\sqrt 3 {a^3}\)
-
B.
\(\dfrac{{16\sqrt 3 }}{9}{a^3}\)
-
C.
\(\dfrac{{16\sqrt 3 }}{3}{a^3}\)
-
D.
\(16\sqrt 3 {a^3}\)
Đề thi THPT QG – 2021 lần 1– mã 104
Cho hàm số \(f\left( x \right) = {x^3} + a{x^2} + bx + c\) với \(a,b,c\) là các số thực. Biết hàm số \(g\left( x \right) = f\left( x \right) + f'\left( x \right) + f''\left( x \right)\) có hai giá trị cực trị là \( - 5\) và \(2.\) Diện tích hình phẳng giới hạn bởi các đường \(y = \dfrac{{f\left( x \right)}}{{g\left( x \right) + 6}}\) và \(y = 1\) bằng
-
A.
\(\ln 3\)
-
B.
\(3\ln 2\)
-
C.
\(\ln 10\)
-
D.
\(\ln 7\)
Đề thi THPT QG – 2021 lần 1– mã 104
Xét các số phức \(z,{\rm{w}}\) thỏa mãn \(\left| z \right| = 1\) và \(\left| {\rm{w}} \right| = 2.\) Khi \(\left| {z + i\overline {\rm{w}} + 6 + 8i} \right|\) đạt giá trị nhỏ nhất, \(\left| {z - {\rm{w}}} \right|\) bằng
-
A.
\(\dfrac{{\sqrt {29} }}{5}\)
-
B.
\(\dfrac{{\sqrt {221} }}{5}\)
-
C.
\(3\) D. \(\sqrt 5 \)
-
D.
\(\sqrt 5 \)
Đề thi THPT QG – 2021 lần 1– mã 104
Trong không gian \(Oxyz,\) cho hai điểm \(A\left( { - 2;1; - 3} \right)\) và \(B\left( {1; - 3;2} \right)\). Xét hai điểm \(M\) và \(N\) thay đổi thuộc mặt phẳng \(\left( {Oxy} \right)\) sao cho \(MN = 3.\) Giá trị lớn nhất của \(\left| {AM - BN} \right|\) bằng
-
A.
\(\sqrt {65} \)
-
B.
\(\sqrt {29} \)
-
C.
\(\sqrt {26} \)
-
D.
\(\sqrt {91} \)
Đề thi THPT QG – 2021 lần 1– mã 104
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = \left( {x - 9} \right)\left( {{x^2} - 16} \right),\,\forall x \in \mathbb{R}.\) Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số \(g\left( x \right) = f\left( {\left| {{x^3} + 7x} \right| + m} \right)\) có ít nhất \(3\) điểm cực trị?
-
A.
\(16\)
-
B.
\(9\)
-
C.
\(4\)
-
D.
\(8\)
Lời giải và đáp án
Đề thi THPT QG – 2021 lần 1– mã 104
Cho hai số phức \(z = 3 + 2i\) và \({\rm{w}} = 1 - 4i\). Số phức \(z + {\rm{w}}\) bằng
-
A.
\(4 + 2i\)
-
B.
\(4 - 2i\)
-
C.
\( - 2 - 6i\)
-
D.
\(2 + 6i\)
Đáp án : B
Áp dụng công thức cộng hai số phức \({z_1} = a + bi\,,\,\,{z_2} = c + di\) thì \({z_1} + {z_2} = \left( {a + c} \right) + \left( {b + d} \right)i\)
Ta có: \(z + {\rm{w}} = 3 + 2i + 1 - 4i = 4 - 2i\)
Đề thi THPT QG – 2021 lần 1– mã 104
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên?
-
A.
\(y = {x^3} - 3x + 1\)
-
B.
\(y = {x^4} + 4{x^2} + 1\)
-
C.
\(y = - {x^3} + 3x + 1\)
-
D.
\(y = - {x^4} + 2{x^2} + 1\)
Đáp án : C
Quan sát thấy đây là đồ thị của hàm số bậc \(3.\)
Dựa vào phần đường cong cuối cùng của đồ thị hàm số để xác định xem hệ số \(a > 0\) hay \(a < 0.\)
Nhận xét giao điểm của đồ thị hàm số với trục tung.
Đồ thị hàm số bậc \(3\) có hệ số \(a < 0\) và đồ thị cắt trục tung tại điểm có tung độ dương nên \(d > 0\)
Đề thi THPT QG – 2021 lần 1– mã 104
Nếu \(\int\limits_1^4 {f\left( x \right)dx = 4} \) và \(\int\limits_1^4 {g\left( x \right)dx = - 3} \) thì \(\int\limits_1^4 {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} \) bằng
-
A.
\(1\)
-
B.
\( - 7\)
-
C.
\( - 1\)
-
D.
\(7\)
Đáp án : D
Áp dụng tính chất của tích phân: \(\int\limits_a^b {\left[ {f\left( x \right) - g\left( x \right)} \right]} \,dx = \int\limits_a^b {f\left( x \right)dx - \int\limits_a^b {g\left( x \right)dx} } \)
Ta có: \(\int\limits_1^4 {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} = \)\(\int\limits_1^4 {f\left( x \right)dx} - \int\limits_1^4 {g\left( x \right)dx = 4 - \left( { - 3} \right) = 7} \)
Đề thi THPT QG – 2021 lần 1– mã 104
Tiệm cận đứng của đồ thị hàm số \(y = \dfrac{{x - 1}}{{x + 2}}\) là đường thẳng có phương trình:\(\)-
A.
\(x = 2\)
-
B.
\(x = - 1\)
-
C.
\(x = - 2\)
-
D.
\(x = 1\)
Đáp án : C
Tiệm cận đứng của đồ thị hàm phân thức bậc nhất \(y = \dfrac{{ax + b}}{{cx + d}}\) là \(x = - \dfrac{d}{c}\)
Tiệm cận đứng của đồ thị hàm số \(y = \dfrac{{x - 1}}{{x + 2}}\) là \(x = - 2\)
Đề thi THPT QG – 2021 lần 1– mã 104
Trong không gian \(Oxyz,\) cho mặt cầu \(\left( S \right)\) có tâm \(I\left( { - 1;3;0} \right)\) và bán kính bằng \(2.\) Phương trình của \(\left( S \right)\) là:
-
A.
\({\left( {x - 1} \right)^2} + {\left( {y + 3} \right)^2} + {z^2} = 2\)
-
B.
\({\left( {x - 1} \right)^2} + {\left( {y + 3} \right)^2} + {z^2} = 4\)
-
C.
\({\left( {x + 1} \right)^2} + {\left( {y - 3} \right)^2} + {z^2} = 4\)
-
D.
\({\left( {x + 1} \right)^2} + {\left( {y - 3} \right)^2} + {z^2} = 2\)
Đáp án : C
Phương trình mặt cầu \(\left( S \right)\) có tâm \(I\left( {a,b,c} \right)\) và bán kính \(R\) là: \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\)
Phương trình mặt cầu \(\left( S \right)\) có tâm \(I\left( { - 1;3;0} \right)\) và bán kính bằng \(2\) là: \({\left( {x + 1} \right)^2} + {\left( {y - 3} \right)^2} + {z^2} = 4\)
-
A.
\(\left( { - \infty ;{{\log }_2}5} \right)\)
-
B.
\(\left( {{{\log }_5}2; + \infty } \right)\)
-
C.
\(\left( { - \infty ;{{\log }_5}2} \right)\)
-
D.
\(\left( {{{\log }_2}5; + \infty } \right)\)
Đáp án : D
Áp dụng cách giải bất phương trình mũ \({a^x} > b \Rightarrow x > {\log _a}b\) với \(0 < a \ne 1,\,b > 0\)
Ta có: \({2^x} > 5 \Leftrightarrow x > {\log _2}5\)
Đề thi THPT QG – 2021 lần 1– mã 104
Thể tích của khối lập phương cạnh \(2a\) bằng:
-
A.
\({a^3}\)
-
B.
\(2{a^3}\)
-
C.
\(8{a^3}\)
-
D.
\(4{a^3}\)
Đáp án : C
Sử dụng công thức tính thể tích khối lập phương cạnh \(a:V = {a^3}\).
Thể tích khối lập phương cạnh \(2a\) là: \(V = {\left( {2a} \right)^3} = 8{a^3}\)
Đề thi THPT QG – 2021 lần 1– mã 104
Trên khoảng \(\left( {0; + \infty } \right),\) đạo hàm của hàm số \(y = {x^{\frac{5}{3}}}\) là:
-
A.
\(y' = \dfrac{3}{8}{x^{\frac{8}{3}}}\)
-
B.
\(y' = \dfrac{5}{3}{x^{\frac{2}{3}}}\)
-
C.
\(y' = \dfrac{5}{3}{x^{ - \frac{2}{3}}}\)
-
D.
\(y' = \dfrac{3}{5}{x^{\frac{2}{3}}}\)
Đáp án : B
Áp dụng công thức tính đạo hàm của hàm số \(y = {x^\alpha } \Rightarrow y' = \alpha .{x^{\alpha - 1}}\).
Ta có: \(\left( {{x^{\frac{5}{3}}}} \right)' = \dfrac{5}{3}.{x^{\frac{2}{3}}}\)
Đề thi THPT QG – 2021 lần 1– mã 104
Trong không gian \(Oxyz,\) cho điểm \(A\left( {2; - 1;4} \right)\). Tọa độ của vectơ \(\overrightarrow {OA} \) là
-
A.
\(\left( { - 2;1;4} \right)\)
-
B.
\(\left( {2; - 1;4} \right)\)
-
C.
\(\left( {2;1;4} \right)\)
-
D.
\(\left( { - 2;1; - 4} \right)\)
Đáp án : B
Tính vectơ \(\overrightarrow {OA} \) với \(O\left( {0;0;0} \right)\)
Ta có: \(\overrightarrow {OA} = \left( {2; - 1;4} \right)\).
Đề thi THPT QG – 2021 lần 1– mã 104
Nếu \(\int\limits_0^3 {f\left( x \right)dx = 3} \) thì \(\int\limits_0^3 {4f\left( x \right)dx} \) bằng
-
A.
\(3\)
-
B.
\(12\)
-
C.
\(36\)
-
D.
\(4\)
Đáp án : B
Áp dụng tính chất tích phân: \(\int\limits_a^b {k.f\left( x \right)dx} = k.\int\limits_a^b {f\left( x \right)dx} \)
Ta có: \(\int\limits_0^3 {4f\left( x \right)dx} = 4\int\limits_0^3 {f\left( x \right)dx = 4.3 = 12} \)
Đề thi THPT QG – 2021 lần 1– mã 104
Cho cấp số nhân \(\left( {{u_n}} \right)\) với \({u_1} = 2\) và \({u_2} = 10\). Công bội của cấp số nhân đã cho bằng
-
A.
\( - 8\)
-
B.
\(8\)
-
C.
\(5\)
-
D.
\(\dfrac{1}{5}\)
Đáp án : C
Áp dụng công thức số hạng tổng quát của cấp số nhân: \({u_n} = {u_1}.{q^{n - 1}}\)
Ta có: \({u_2} = {u_1}.q \Rightarrow q = \dfrac{{10}}{2} = 5\)
Đề thi THPT QG – 2021 lần 1– mã 104
Với \(n\) là số nguyên dương bất kì, \(n \ge 3,\) công thức nào dưới đây đúng?
-
A.
\(A_n^3 = \dfrac{{\left( {n - 3} \right)!}}{{n!}}\)
-
B.
\(A_n^3 = \dfrac{{3!}}{{\left( {n - 3} \right)!}}\)
-
C.
\(A_n^3 = \dfrac{{n!}}{{\left( {n - 3} \right)!}}\)
-
D.
\(A_n^3 = \dfrac{{n!}}{{3!\left( {n - 3} \right)!}}\)
Đáp án : C
Áp dụng công thức tính chỉnh hợp \(A_n^k = \dfrac{{n!}}{{\left( {n - k} \right)!}}\)
Ta có \(A_n^3 = \dfrac{{n!}}{{\left( {n - 3} \right)!}}\)
Đề thi THPT QG – 2021 lần 1– mã 104
Cho hàm số \(f\left( x \right) = {x^2} + 2.\) Khẳng định nào dưới đây đúng?
-
A.
\(\int {f\left( x \right)dx = 2x + C} \)
-
B.
\(\int {f\left( x \right)dx = \dfrac{{{x^3}}}{3} + 2x + C} \)
-
C.
\(\int {f\left( x \right)dx = {x^2} + 2x + C} \)
-
D.
\(\int {f\left( x \right)dx = {x^3} + 2x + C} \)
Đáp án : B
Áp dụng công thức tính nguyên hàm của các hàm số.
Ta có \(\int {\left( {{x^2} + 2} \right)dx = \dfrac{{{x^3}}}{3} + 2x + C.} \)
Đề thi THPT QG – 2021 lần 1– mã 104
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
Giá trị cực tiểu của hàm số đã cho bằng
-
A.
\(0\)
-
B.
\(3\)
-
C.
\(1\)
-
D.
\( - 1\)
Đáp án : C
Quan sát bảng biến thiên để tìm điểm cực tiểu của hàm số, từ đó suy ra giá trị cực tiểu.
Ta có tại điểm cực tiểu \(x = 0\), hàm số có giá trị \(y = 1\)
Đề thi THPT QG – 2021 lần 1– mã 104
Trong không gian \(Oxyz,\) cho mặt phẳng \(\left( P \right):2x + 4y - z - 1 = 0.\) Vectơ nào dưới đây là một vectơ pháp tuyến của \(\left( P \right)?\)
-
A.
\(\overrightarrow {{n_2}} = \left( {2; - 4;1} \right)\)
-
B.
\(\overrightarrow {{n_1}} = \left( {2;4;1} \right)\)
-
C.
\(\overrightarrow {{n_3}} = \left( {2;4; - 1} \right)\)
-
D.
\(\overrightarrow {{n_4}} = \left( { - 2;4;1} \right)\)
Đáp án : C
Phương trình mặt phẳng \(\left( P \right):ax + by + cz + d = 0\) có một vtpt là \(\overrightarrow n = \left( {a;b;c} \right)\)
Mặt phẳng \(\left( P \right):2x + 4y - z - 1 = 0\) có vtpt là \(\overrightarrow n = \left( {2;4; - 1} \right)\)
-
A.
\(2\)
-
B.
\( - 4\)
-
C.
\(4\)
-
D.
\( - 2\)
Đáp án : C
Số phức \(z = a + bi,\,\left( {a,b \in \mathbb{R}} \right)\) có phần thực là \(a.\)
Phần thực của số phức \(z = 4 - 2i\) bằng \(4.\)
Đề thi THPT QG – 2021 lần 1– mã 104
Nghiệm của phương trình \({\log _2}\left( {5x} \right) = 3\) là
-
A.
\(x = \dfrac{8}{5}\)
-
B.
\(x = \dfrac{9}{5}\)
-
C.
\(x = 8\)
-
D.
\(x = 9\)
Đáp án : A
Sử dụng cách giải phương trình logarit \({\log _a}u = b \Leftrightarrow u = {a^b},\,\,\left( {0 < a \ne 1;\,u > 0} \right)\)
ĐKXĐ: \(x > 0\)
Ta có: \({\log _2}\left( {5x} \right) = 3 \Leftrightarrow 5x = {2^3} = 8 \Leftrightarrow x = \dfrac{8}{5}\,\left( {TMDK} \right)\)
-
A.
\(\mathbb{R}\backslash \left\{ 0 \right\}\)
-
B.
\(\mathbb{R}\)
-
C.
\(\left[ {0; + \infty } \right)\)
-
D.
\(\left( {0; + \infty } \right)\)
Đáp án : B
Tập xác định của hàm số mũ \(y = {a^x}\) là \(\mathbb{R}\)
Tập xác định của hàm số \(y = {8^x}\) là \(\mathbb{R}\)
Đề thi THPT QG – 2021 lần 1– mã 104
Cho \(a > 0\) và \(a \ne 1,\) khi đó \({\log _a}\sqrt[5]{a}\) bằng
-
A.
\(\dfrac{1}{5}\)
-
B.
\( - \dfrac{1}{5}\)
-
C.
\(5\)
-
D.
\( - 5\)
Đáp án : A
Sử dụng công thức biến đổi logarit: \({\log _a}{b^\alpha } = \alpha .{\log _a}b\)
Ta có: \({\log _a}\sqrt[5]{a} = \dfrac{1}{5}{\log _a}a = \dfrac{1}{5}\)
Đề thi THPT QG – 2021 lần 1– mã 104
Trong không gian \(Oxyz,\) cho đường thẳng \(d\) đi qua điểm \(M\left( {1;5; - 2} \right)\) và có một vectơ chỉ phương \(\overrightarrow u = \left( {3; - 6;1} \right).\) Phương trình của \(d\) là:
-
A.
\(\left\{ \begin{array}{l}x = 3 + t\\y = - 6 + 5t\\z = 1 - 2t\end{array} \right.\)
-
B.
\(\left\{ \begin{array}{l}x = 1 + 3t\\y = 5 - 6t\\z = 2 + t\end{array} \right.\)
-
C.
\(\left\{ \begin{array}{l}x = 1 + 3t\\y = 5 + 6t\\z = - 2 + t\end{array} \right.\)
-
D.
\(\left\{ \begin{array}{l}x = 1 + 3t\\y = 5 - 6t\\z = - 2 + t\end{array} \right.\)
Đáp án : D
Phương trình đường thẳng đi qua \(M\left( {{x_0};{y_0};{z_0}} \right)\) và có vtcp \(\overrightarrow u = \left( {a;b;c} \right)\) sẽ có phương trình tham số là:
\(\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\\z = {z_0} + ct\end{array} \right.\)
Ta có phương trình đường thẳng \(d\) đi qua điểm \(M\left( {1;5; - 2} \right)\) và có một vectơ chỉ phương \(\overrightarrow u = \left( {3; - 6;1} \right)\) là:
\(\left\{ \begin{array}{l}x = 1 + 3t\\y = 5 - 6t\\z = - 2 + t\end{array} \right.\)
Đề thi THPT QG – 2021 lần 1– mã 104
Trên mặt phẳng tọa độ, điểm \(M\left( { - 4;3} \right)\) là điểm biểu diễn của số phức nào dưới đây?
-
A.
\({z_3} = - 4 - 3i\)
-
B.
\({z_4} = 4 + 3i\)
-
C.
\({z_2} = 4 - 3i\)
-
D.
\({z_1} = - 4 + 3i\)
Đáp án : D
Số phức \(z = a + bi\) có điểm biểu diễn là \(M\left( {a;b} \right)\).
Ta có: điểm \(M\left( { - 4;3} \right)\) là điểm biểu diễn của số phức \({z_1} = - 4 + 3i\).
Đề thi THPT QG – 2021 lần 1– mã 104
Cho hàm số \(f\left( x \right)\) có bảng xét dấu của đạo hàm như sau:
Số điểm cực trị của hàm số đã cho là
-
A.
\(3\)
-
B.
\(4\)
-
C.
\(2\)
-
D.
\(5\)
Đáp án : B
Số điểm cực trị của hàm số là số điểm mà qua đó đạo hàm đổi dấu.
Ta có \(f'\left( x \right)\) đổi dấu qua \(x = - 2;\,\,x = - 1;\,\,x = 2;\,\,x = 4\) nên hàm số có \(4\) điểm cực trị.
Đề thi THPT QG – 2021 lần 1– mã 104
Cho hàm số \(f\left( x \right) = {e^x} + 4\). Khẳng định nào dưới đây đúng?
-
A.
\(\int {f\left( x \right)dx = {e^x} + 4x + C.} \)
-
B.
\(\int {f\left( x \right)dx = {e^x} + C.} \)
-
C.
\(\int {f\left( x \right)dx = {e^{x - 4}} + C.} \)
-
D.
\(\int {f\left( x \right)dx = {e^x} - 4x + C.} \)
Đáp án : A
Áp dụng công thức nguyên hàm của các hàm số.
Ta có: \(\int {\left( {{e^x} + 4} \right)dx = {e^x} + 4x + C.} \)
Đề thi THPT QG – 2021 lần 1– mã 104
Cho hàm số \(y = f\left( x \right)\) có đồ thị là đường cong trong hình bên. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
-
A.
\(\left( { - 1;1} \right)\)
-
B.
\(\left( {1; + \infty } \right)\)
-
C.
\(\left( { - \infty ;1} \right)\)
-
D.
\(\left( {0;3} \right)\)
Đáp án : A
Trên khoảng mà phần đường cong của đồ thị hàm số đi xuống thì hàm số nghịch biến.
Ta có trên khoảng \(\left( { - 1;1} \right)\) hàm số nghịch biến.
Đề thi THPT QG – 2021 lần 1– mã 104
Diện tích \(S\) của mặt cầu bán kính \(R\) được tính theo công thức nào dưới đây?
-
A.
\(S = \pi {R^2}\)
-
B.
\(S = 16\pi {R^2}\)
-
C.
\(S = 4\pi {R^2}\)
-
D.
\(S = \dfrac{4}{3}\pi {R^2}\)
Đáp án : C
Áp dụng công thức tính bán kính mặt cầu.
Ta có: \(S = 4\pi {R^2}\)
Đề thi THPT QG – 2021 lần 1– mã 104
Đồ thị của hàm số \(y = - 2{x^3} + 3{x^2} - 5\) cắt trục tung tại điểm có tung độ bằng
-
A.
\( - 5\)
-
B.
\(0\)
-
C.
\( - 1\)
-
D.
\(2\)
Đáp án : A
Giao điểm của đồ thị hàm số với trục tung là điểm \(A\left( {0;b} \right)\)
Ta có đồ thị của hàm số \(y = - 2{x^3} + 3{x^2} - 5\) cắt trục tung tại điểm có tung độ \(y = - 5\)
Đề thi THPT QG – 2021 lần 1– mã 104
Cho khối chóp có diện tích đáy \(B = 8{a^2}\) và chiều cao \(h = a\). Thể tích của khối chóp đã cho bằng
-
A.
\(8{a^3}\)
-
B.
\(\dfrac{4}{3}{a^3}\)
-
C.
\(4{a^3}\)
-
D.
\(\dfrac{8}{3}{a^3}\)
Đáp án : D
Áp dụng công thức tính thể tích khối chóp.
Ta có: \(V = \dfrac{1}{3}.B.h = \dfrac{8}{3}{a^3}\)
Đề thi THPT QG – 2021 lần 1– mã 104
Cho khối trụ có bán kính đáy \(r = 5\) và chiều cao \(h = 3\). Thể tích của khối trụ đã cho bằng
-
A.
\(15\pi \)
-
B.
\(75\pi \)
-
C.
\(25\pi \)
-
D.
\(45\pi \)
Đáp án : B
Áp dụng công thức tính thể tích của khối trụ.
Ta có: \(V = \pi {r^2}h = \pi {.5^2}.3 = 75\pi \)
Đề thi THPT QG – 2021 lần 1– mã 104
Trong không gian \(Oxyz,\) cho điểm \(M\left( {2;1; - 2} \right)\) và mặt phẳng \(\left( P \right):3x + 2y - z + 1 = 0\). Đường thẳng đi qua \(M\) và vuông góc với \(\left( P \right)\) có phương trình là:
-
A.
\(\dfrac{{x - 2}}{3} = \dfrac{{y - 1}}{2} = \dfrac{{z + 2}}{{ - 1}}\)
-
B.
\(\dfrac{{x - 2}}{3} = \dfrac{{y - 1}}{2} = \dfrac{{z + 2}}{1}\)
-
C.
\(\dfrac{{x + 2}}{3} = \dfrac{{y + 1}}{2} = \dfrac{{z - 2}}{1}\)
-
D.
\(\dfrac{{x + 2}}{3} = \dfrac{{y + 1}}{2} = \dfrac{{z - 2}}{{ - 1}}\)
Đáp án : A
Đường thẳng vuông góc với mặt phẳng thì vtcp của đường thẳng đó chính là vtpt của mặt phẳng ( \({\overrightarrow u _d} = {\overrightarrow n _{\left( P \right)}}\))
Viết phương trình chính tắc của đường thẳng qua điểm \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) và có \(\overrightarrow u = \left( {a;b;c} \right)\) là vtcp:
\(\dfrac{{x - {x_0}}}{a} = \dfrac{{y - {y_0}}}{b} = \dfrac{{z - {z_0}}}{c}\)
Ta có: \({\overrightarrow u _d} = {\overrightarrow n _{\left( P \right)}} = \left( {3;2; - 1} \right)\)
Đường thẳng đi qua \(M\) và vuông góc với \(\left( P \right)\) có phương trình là: \(\dfrac{{x - 2}}{3} = \dfrac{{y - 1}}{2} = \dfrac{{z + 2}}{{ - 1}}\)
Đề thi THPT QG – 2021 lần 1– mã 104
Cho hình lăng trụ đứng \(ABC.A'B'C'\) có tất cả các cạnh bằng nhau (tham khảo hình bên). Góc giữa hai đường thẳng \(AB'\) và \(CC'\) bằng
-
A.
\({30^o}\)
-
B.
\({90^o}\)
-
C.
\({60^o}\)
-
D.
\({45^o}\)
Đáp án : D
Sử dụng phương pháp xác định góc giữa hai đường thẳng chéo nhau: Tìm một đường thẳng song song với đường này và cắt đường kia.
Ta lấy giá trị góc tạo thành ( nếu góc \( < {90^o}\)) và lấy giá trị bù với góc đó ( nếu góc \( > {90^o}\))
Ta có: \(BB'//CC' \Rightarrow \angle \left( {AB',CC'} \right) = \angle \left( {AB',B'B} \right) = \angle AB'B\)
Mà \(ABC.A'B'C'\) là hình lăng trụ đứng có tất cả các cạnh bằng nhau nên mặt bên là hình vuông \( \Rightarrow \angle AB'B = {45^o}\)
Đề thi THPT QG – 2021 lần 1– mã 104
Cho hình chóp \(S.ABC\) có đáy là tam giác vuông cân tại \(B,\) \(AB = 4a\) và \(SA\) vuông góc với mặt phẳng đáy. Khoảng cách từ \(C\) đến mặt phẳng \(\left( {SAB} \right)\) bằng
-
A.
\(4a\)
-
B.
\(4\sqrt 2 a\)
-
C.
\(2\sqrt 2 a\)
-
D.
\(2a\)
Đáp án : A
Tìm hình chiếu vuông góc của điểm \(C\) lên mp \(\left( {SAB} \right)\).
Tính độ dài đoạn thẳng.
Ta có: \(\left\{ \begin{array}{l}CB \bot AB\\CB \bot SA\end{array} \right. \Rightarrow CB \bot \left( {SAB} \right)\)
Do đó \(d\left( {C,\left( {SAB} \right)} \right) = BC = AB = 4a\) (do tam giác \(ABC\) vuông cân tại \(B\))
Đề thi THPT QG – 2021 lần 1– mã 104
Nếu \(\int\limits_0^2 {f\left( x \right)dx = 4} \) thì \(\int\limits_0^2 {\left[ {2f\left( x \right) - 1} \right]dx} \) bằng
-
A.
\(8\)
-
B.
\(10\)
-
C.
\(7\)
-
D.
\(6\)
Đáp án : D
Áp dụng tính chất của tích phân.
Ta có: \(\int\limits_0^2 {\left[ {2f\left( x \right) - 1} \right]dx = 2\int\limits_0^2 {f\left( x \right)dx - \int\limits_0^2 {1dx = 2.4 - 2 = 6} } } \)
Đề thi THPT QG – 2021 lần 1– mã 104
Biết hàm số \(y = \dfrac{{x + a}}{{x - 1}}\) \((a\) là số thực cho trước, \(a \ne 1)\) có đồ thị như trong hình bên. Mệnh đề nào dưới đây đúng?
-
A.
(y' < 0,\,\forall x \in \mathbb{R}\)
-
B.
\(y' < 0,\,\forall x \ne 1\)
-
C.
\(y' > 0,\,\forall x \in \mathbb{R}\)
-
D.
\(y' > 0,\,\forall x \ne 1\)
Đáp án : B
Quan sát phần đường cong đồ thị hàm số, nếu đường cong đi xuống thì hàm số nghịch biến trên khoảng xác định, nếu đường cong đi lên thì hàm số đồng biến trên khoảng xác định.
Ta có đồ thị hàm số có đường cong đi xuống nên \(y' < 0,\,\forall x \ne 1\)
Đề thi THPT QG – 2021 lần 1– mã 104
Cho số phức \(z\) thỏa mãn \(iz = 4 + 3i.\) Số phức liên hợp của \(z\) là
-
A.
\(\overline z = 3 + 4i\)
-
B.
\(\overline z = - 3 - 4i\)
-
C.
\(\overline z = 3 - 4i\)
-
D.
\(\overline z = - 3 + 4i\)
Đáp án : A
Từ đẳng thức ban đầu ta tìm được số phức \(z.\)
Số phức liên hợp của \(z = a + bi\) là \(\overline z = a - bi\,\,\left( {a,b \in \mathbb{R}} \right)\)
Ta có: \(iz = 4 + 3i \Rightarrow z = 3 - 4i\)
Số phức liên hợp của \(z\) là \(\overline z = 3 + 4i\)
Đề thi THPT QG – 2021 lần 1– mã 104
Từ một hộp chứa \(12\) quả bóng gồm \(5\) quả màu đỏ và \(7\) quả màu xanh, lấy ngẫu nhiên đồng thời \(3\) quả. Xác suất để lấy được \(3\) quả màu đỏ bằng
-
A.
\(\dfrac{1}{{22}}\)
-
B.
\(\dfrac{7}{{44}}\)
-
C.
\(\dfrac{5}{{12}}\)
-
D.
\(\dfrac{2}{7}\)
Đáp án : A
Sử dụng quy tắc đếm, tổ hợp, chỉnh hợp.
Tính xác suất của biến cố \(A\) theo công thức \(P\left( A \right) = \dfrac{{n\left( A \right)}}{{n\left( \Omega \right)}}\).
Chọn \(3\) quả từ hộp chứa \(12\) quả bóng ta có: \(C_{12}^3\) cách chọn
Gọi \(A\) là biến cố chọn được \(3\) quả màu đó.
Khi đó \(n\left( A \right) = C_5^3\)
Vậy \(P\left( A \right) = \dfrac{{C_5^3}}{{C_{12}^3}} = \dfrac{1}{{22}}\)
Đề thi THPT QG – 2021 lần 1– mã 104
Với mọi \(a,b\) thỏa mãn \({\log _2}{a^3} + {\log _2}b = 5,\) khẳng định nào dưới đây đúng?
-
A.
\({a^3}b = 32\)
-
B.
\({a^3}b = 25\)
-
C.
\({a^3} + b = 25\)
-
D.
\({a^3} + b = 32\)
Đáp án : A
Áp dụng các công thức biến đổi logarit.
Ta có: \({\log _2}{a^3} + {\log _2}b = 5 \Rightarrow {\log _2}{a^3}b = 5 \Rightarrow {a^3}b = {2^5} = 32\)
Đề thi THPT QG – 2021 lần 1– mã 104
Trên đoạn \(\left[ { - 1;2} \right],\) hàm số \(y = {x^3} + 3{x^2} + 1\) đạt giá trị nhỏ nhất tại điểm
-
A.
\(x = 2\)
-
B.
\(x = 0\)
-
C.
\(x = - 1\)
-
D.
\(x = 1\)
Đáp án : B
Tính đạo hàm \(y'\) và tìm nghiệm của phương trình \(y' = 0\)
Tính giá trị của hàm số tại hai đầu mút và tại điểm \(y' = 0\)
Ta có: \(y' = 3{x^2} + 6x = 0 \Rightarrow \left[ \begin{array}{l}x = 0\, \in \left[ { - 1;2} \right]\\x = -2\, \notin \left[ { - 1;2} \right]\end{array} \right.\)
\(y\left( { - 1} \right) = 3;\,\,y\left( 0 \right) = 1\,\,;\,y\left( 2 \right) = 21\)
Hàm số đạt giá trị nhỏ nhất tại điểm \(x = 0\).
Đề thi THPT QG – 2021 lần 1– mã 104
Trong không gian \(Oxyz,\) cho hai điểm \(A\left( {1;0;0} \right)\) và \(B\left( {3;2;1} \right).\) Mặt phẳng đi qua \(A\) và vuông góc với \(AB\) có phương trình là:
-
A.
\(2x + 2y + z - 2 = 0\)
-
B.
\(4x + 2y + z - 17 = 0\)
-
C.
\(4x + 2y + z - 4 = 0\)
-
D.
\(2x + 2y + z - 11 = 0\)
Đáp án : A
Mặt phẳng vuông góc với đường thẳng thì vtpt của mặt phẳng chính là vtcp của đường thẳng.
Lập phương trình mặt phẳng \(\left( P \right)\) đi qua \(M\left( {{x_0};{y_0};{z_0}} \right)\) và có vtpt \(\overrightarrow n = \left( {a;b;c} \right)\) là:
\(\left( P \right):\,\,\,a\left( {x - {x_0}} \right) + b\left( {y - {y_0}} \right) + c\left( {z - {z_0}} \right) = 0\)
Ta có: \(\overrightarrow {AB} = \left( {2;2;1} \right)\)
Mặt phẳng đi qua \(A\) và vuông góc với \(AB\) có phương trình là: \(2x + 2y + z - 2 = 0\)
Đề thi THPT QG – 2021 lần 1– mã 104
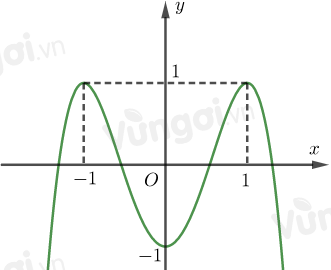
Cho hàm số bậc bốn \(y = f\left( x \right)\) có đồ thị là đường cong trong hình trên. Số nghiệm thực phân biệt của phương trình \(f\left( {f\left( x \right)} \right) = 0\) là
-
A.
\(12\)
-
B.
\(10\)
-
C.
\(8\)
-
D.
\(4\)
Đáp án : B
Tìm nghiệm của phương trình \(f\left( t \right) = 0\) \(\begin{array}{l} \Rightarrow \left[ \begin{array}{l}t = {t_1}\\t = {t_2}\\...\end{array} \right.\\\end{array}\)
Tìm nghiệm của phương trình \(\left[ \begin{array}{l}f\left( x \right) = {t_1}\\f\left( x \right) = {t_2}\\...\end{array} \right.\)
Ta có: \(f\left( {f\left( x \right)} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = a\,\,\,\left( {a < - 1} \right)\\f\left( x \right) = b\,\,\,\left( { - 1 < b < 0} \right)\\f\left( x \right) = c\,\,\,\left( {0 < c < 1} \right)\\f\left( x \right) = d\,\,\,\left( {d > 1} \right)\end{array} \right.\)
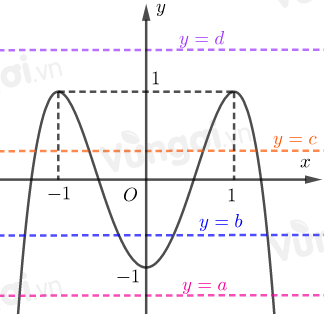
Dựa vào đồ thị ta thấy:
\(f\left( x \right) = a\) với \(a < - 1\) có \(2\) nghiệm.
\(f\left( x \right) = b\,\,\left( { - 1 < b < 0} \right)\) có \(4\) nghiệm.
\(f\left( x \right) = c\) với \(0 < c < 1\) có \(4\) nghiệm.
\(f\left( x \right) = d\) với \(d > 1\) vô nghiệm.
Số nghiệm thực phân biệt của phương trình \(f\left( {f\left( x \right)} \right) = 0\) là \(10.\)
Đề thi THPT QG – 2021 lần 1– mã 104
Có bao nhiêu số nguyên \(x\) thỏa mãn \(\left( {{2^{{x^2}}} - {4^x}} \right)\left[ {{{\log }_3}\left( {x + 25} \right) - 3} \right] \le 0\)?
-
A.
\(24\)
-
B.
vô số
-
C.
\(25\)
-
D.
\(26\)
Đáp án : D
Tích của hai biểu thức \( \le 0\) nên hai biểu thức trái dấu, ta chia hai trường hợp.
Từ mỗi trường hợp ta giải ra các giá trị \(x\)
Đối chiếu với điều kiện xác định.
Điều kiện xác định \(x > - 25\)
TH1: \(\left\{ \begin{array}{l}{2^{{x^2}}} - {4^x} \le 0\\{\log _3}\left( {x + 25} \right) - 3 \ge 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{2^{{x^2}}} \le {4^x}\\{\log _3}\left( {x + 25} \right) \ge 3\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x^2} \le 2x\\x + 25 \ge 27\end{array} \right. \Rightarrow \left\{ \begin{array}{l}0 \le x \le 2\\x \ge 2\end{array} \right. \Rightarrow x = 2\)
TH2: \(\left\{ \begin{array}{l}{2^{{x^2}}} - {4^x} \ge 0\\{\log _3}\left( {x + 25} \right) - 3 \le 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{2^{{x^2}}} \ge {4^x}\\x + 25 \le {3^3}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x^2} \ge 2x\\x \le 2\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}x \le 0\\x \ge 2\end{array} \right.\\x \le 2\end{array} \right.\)
Kết hợp với điều kiện \(x > - 25\) ta có \(x \in \left\{ { - 24; - 23;...;0} \right\}\) => Có 25 giá trị
Vậy từ 2 trường hợp trên ta có 26 giá trị của $x$ thỏa mãn bài toán.
Đề thi THPT QG – 2021 lần 1– mã 104
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}2x + 2\,\,\,\,\,khi\,\,x \ge 1\\3{x^2} + 1\,\,\,khi\,\,x < 1\end{array} \right..\) Giả sử \(F\) là nguyên hàm của \(f\) trên \(\mathbb{R}\) thỏa mãn \(F\left( 0 \right) = 2\). Giá trị của \(F\left( { - 1} \right) + 2F\left( 2 \right)\) bằng
-
A.
\(18\)
-
B.
\(20\)
-
C.
\(9\)
-
D.
\(24\)
Đáp án : A
Tính nguyên hàm của \(f\left( x \right)\) khi \(x < 1\).
Tính tích phân của \(\int\limits_{ - 1}^1 {f\left( x \right)dx} \) và \(\int\limits_1^2 {f\left( x \right)dx} \), từ đó tính được \(F\left( { - 1} \right)\) và \(F\left( 2 \right)\).
Ta có: \(I = \int\limits_0^{ - 1} {f\left( x \right)dx + 2\int\limits_0^2 {f\left( x \right)dx = F\left( { - 1} \right) - F\left( 0 \right) + 2F\left( 2 \right) - 2F\left( 0 \right)} } \)
Do đó \(I = F\left( { - 1} \right) + 2F\left( 2 \right) - 3F\left( 0 \right) = F\left( { - 1} \right) + 2F\left( 2 \right) - 6 \Rightarrow F\left( { - 1} \right) + 2F\left( 2 \right) = I + 6\)
Mà \(\int\limits_0^{ - 1} {f\left( x \right)dx = - \int\limits_{ - 1}^0 {\left( {3{x^2} + 1} \right)dx = - 2} } \) và \(2\int\limits_0^2 {f\left( x \right)dx = } 2\left( {\int\limits_0^1 {\left( {3{x^2} + 1} \right)dx + \int\limits_1^2 {\left( {2x + 2} \right)dx} } } \right) = 14\)
Suy ra \(I = - 2 + 14 = 12\)
Do đó \(F\left( { - 1} \right) + 2F\left( 2 \right) = 12 + 6 = 18\).
Đề thi THPT QG – 2021 lần 1– mã 104
Cắt hình nón \(\left( \aleph \right)\) bởi mặt phẳng đi qua đỉnh và tạo với mặt phẳng chứa đáy một góc bằng \({30^o}\), ta được thiết diện là tam giác đều cạnh \(2a.\) Diện tích xung quanh của \(\left( \aleph \right)\) bằng
-
A.
\(\sqrt 7 \pi {a^2}\)
-
B.
\(\sqrt {13} \pi {a^2}\)
-
C.
\(2\sqrt {13} \pi {a^2}\)
-
D.
\(2\sqrt 7 \pi {a^2}\)
Đáp án : B
Áp dụng phương pháp xác định góc giữa hai mặt phẳng để xác định góc giữa đáy và mặt phẳng qua đỉnh.
Từ đó tìm được mối quan hệ giữa chiều cao của hình nón và bán kính đáy.
Biến đổi, tính toán để tìm được bán kính đáy.
Áp dụng công thức tính diện tích xung quanh nón: \({S_{xq}} = \pi rl.\)
Gọi mặt phẳng đi qua đỉnh của hình nón là \(\left( {SMN} \right)\).
Do thiết diện của \(\left( {SMN} \right)\) và hình nón là tam giác đều cạnh \(2a\) nên \(SM = MN = SN = 2a\)
Kẻ \(OH \bot AB\). Nối \(S\) với \(H.\)
Khi đó \(H\) là trung điểm \(MN\) nên \(SH = a\sqrt 3 \)
Ta có: góc giữa \(\left( {SMN} \right)\) và mặt đáy là \(\angle SHO\)
Trong tam giác \(SHO\) vuông tại \(O\) ta có: \(\tan SHO = \dfrac{{SO}}{{OH}}\)\( \Rightarrow \tan {30^o} = \dfrac{{SO}}{{OH}} \Rightarrow SO = \dfrac{{\sqrt 3 }}{3}.OH\)
Theo định lí py-ta-go ta có: \(S{O^2} + O{H^2} = S{H^2}\)\( \Rightarrow \dfrac{4}{3}O{H^2} = S{H^2} \Rightarrow OH = \dfrac{{\sqrt 3 }}{2}SH = \dfrac{{3a}}{2}\)
\( \Rightarrow SO = \dfrac{{\sqrt 3 }}{2}a\)\( \Rightarrow OM = \sqrt {S{M^2} - S{O^2}} = \sqrt {4{a^2} - \dfrac{{3{a^2}}}{4}} = \dfrac{{a\sqrt {13} }}{2}\)
Diện tích xung quanh của hình nón: \({S_{xq}} = \pi .\dfrac{{a\sqrt {13} }}{2}.2a = \pi \sqrt {13} {a^2}\)
Đề thi THPT QG – 2021 lần 1– mã 104
Trong không gian \(Oxyz,\) cho đường thẳng \(d:\dfrac{x}{1} = \dfrac{y}{{ - 1}} = \dfrac{{z - 1}}{2}\) và mặt phẳng \(\left( P \right):x + 2y - 2z + 2 = 0\). Hình chiếu vuông góc của \(d\) trên \(\left( P \right)\) là đường thẳng có phương trình:
-
A.
\(\dfrac{x}{{ - 2}} = \dfrac{y}{4} = \dfrac{{z - 1}}{3}\)
-
B.
\(\dfrac{x}{{14}} = \dfrac{y}{1} = \dfrac{{z + 1}}{8}\)
-
C.
\(\dfrac{x}{{ - 2}} = \dfrac{y}{4} = \dfrac{{z + 1}}{3}\)
-
D.
\(\dfrac{x}{{14}} = \dfrac{y}{1} = \dfrac{{z - 1}}{8}\)
Đáp án : D
Tìm giao điểm \(I\) của đường thẳng \(d\) và mặt phẳng \(\left( P \right).\)
Lấy điểm \(A\) bất kì thuộc đường thẳng \(d.\) Lập phương trình đường thẳng \(\Delta \) đi qua \(A\).
Tìm tọa độ giao điểm \(H\) của \(\Delta \) và \(\left( P \right).\)
Đường thẳng \(IH\) chính là hình chiếu vuông góc của \(d\) trên \(\left( P \right).\)
Gọi giao điểm của \(d\) và mặt phẳng \(\left( P \right)\) là điểm \(I.\)
Do \(I \in d \Rightarrow I\left( {t; - t;1 + 2t} \right)\). Mà \(I \in \left( P \right)\)
\( \Rightarrow t - 2t - 2\left( {1 + 2t} \right) + 2 = 0 \Rightarrow - 5t = 0 \Rightarrow t = 0 \Rightarrow I\left( {0;0;1} \right)\)
Lấy \(A\left( {1; - 1;3} \right) \in d\).Gọi \(\Delta \) là đường thẳng qua \(A\) và vuông góc với \(\left( P \right) \Rightarrow {\overrightarrow u _\Delta } = {\overrightarrow n _{\left( P \right)}} = \left( {1;2; - 2} \right)\)
Phương trình đường thẳng \(\Delta :\left\{ \begin{array}{l}x = 1 + t\\y = - 1 + 2t\\z = 3 - 2t\end{array} \right.\)
Gọi \(H\) là giao điểm của \(\Delta \) và \(\left( P \right)\)\( \Rightarrow H\left( {1 + t; - 1 + 2t;3 - 2t} \right)\)
Mà \(H \in \left( P \right) \Rightarrow 1 + t + 2\left( { - 1 + 2t} \right) - 2\left( {3 - 2t} \right) + 2 = 0\)\( \Rightarrow 9t = 5 \Rightarrow t = \dfrac{5}{9}\)\( \Rightarrow H\left( {\dfrac{{14}}{9};\dfrac{1}{9};\dfrac{{17}}{9}} \right)\)
Ta có: \(\overrightarrow {IH} = \left( {\dfrac{{14}}{9};\dfrac{1}{9};\dfrac{8}{9}} \right)\)
Phương trình đường thẳng \(d'\) qua \(I\) và nhận \(9\overrightarrow {IH} \) làm vtcp: \(\dfrac{x}{{14}} = \dfrac{y}{1} = \dfrac{{z - 1}}{8}\)
Đề thi THPT QG – 2021 lần 1– mã 104
Có bao nhiêu số nguyên \(y\) sao cho tồn tại \(x \in \left( {\dfrac{1}{3};6} \right)\) thỏa mãn \({27^{3{x^2} + xy}} = \left( {1 + xy} \right){27^{18x}}\)
-
A.
\(19\)
-
B.
\(20\)
-
C.
\(18\)
-
D.
\(21\)
Đáp án : B
Biến đổi đẳng thức ban đầu, đặt \(f\left( x \right) = g\left( y \right)\)
Xét trường hợp \(y = 0\) và \(y \ne 0\). Ta khảo sát hàm \(f\left( x \right)\) và chỉ ra tập giá trị của \(y\) thỏa mãn.
Ta có: \({27^{3{x^2} + xy - 18x}} = xy + 1\)
ĐK: \(xy + 1 > 0 \Leftrightarrow y > - \dfrac{1}{x}\) khi \(x \in \left( {\dfrac{1}{3};6} \right)\)\( \Rightarrow y > - 3\) thì mới tồn tại \(x \in \left( {\dfrac{1}{3};6} \right)\).
Xét \({27^{3{x^2} + xy - 18x}} - xy - 1 = 0\)
Đặt \(f\left( x \right) = g\left( y \right) = {27^{3{x^2} + xy - 18x}} - xy - 1\) ta có: \(\left\{ \begin{array}{l}f\left( {\dfrac{1}{3}} \right) = {3^{y - 17}} - \dfrac{y}{3} - 1\\f\left( 6 \right) = {27^{6y}} - 6y - 1\end{array} \right.\)
Nhận thấy \(f\left( 6 \right) \ge 0\,\forall \,y \in \mathbb{Z}\). Dấu bằng xảy ra khi \(y = 0\).
Xét \(y = 0\) thay vào phương trình ban đầu \( \Rightarrow \left[ \begin{array}{l}x = 0\\x = 6\end{array} \right.\) loại vì \(x \in \left( {\dfrac{1}{3};6} \right)\)
Xét \(y \ne 0 \Rightarrow f\left( 6 \right) > 0\,\forall \,x \in \mathbb{Z}*\)
Ta table khảo sát \(f\left( {\dfrac{1}{3}} \right)\) ta rút ra được \(f\left( {\dfrac{1}{3}} \right) < 0,\,\forall y \in \left\{ { - 2; - 1;1;2;...;17;18} \right\}\).
Ta có: \(f\left( {\dfrac{1}{3}} \right).f\left( 6 \right) < 0\,\forall \,y \in \left\{ { - 2; - 1;1;2;...;18} \right\}\)
Có \(20\) giá trị của \(y\) để tồn tại nghiệm \(x \in \left( {\dfrac{1}{3};6} \right)\)
Từ bảng Table ta nhận thấy khi \(y \ge 19\) thì phương trình vô nghiệm.
\(g'\left( y \right) = x\left( {{{27}^{3{x^2} + x\left( {y - 18} \right)}}.\ln 27 - 1} \right) > 0 \Rightarrow \left\{ \begin{array}{l}\forall y \ge 19\\x \in \left( {\dfrac{1}{3};6} \right)\end{array} \right.\)
Vậy có \(20\) giá trị nguyên của \(y\) thỏa mãn.
Đề thi THPT QG – 2021 lần 1– mã 104
Trên tập hợp các số phức, xét phương trình \({z^2} - 2\left( {m + 1} \right)z + {m^2} = 0\)\((m\) là tham số thực). Có bao nhiêu giá trị của \(m\) để phương trình đó có nghiệm \({z_0}\) thỏa mãn \(\left| {{z_0}} \right| = 6\)?
-
A.
\(4\)
-
B.
\(1\)
-
C.
\(2\)
-
D.
\(3\)
Đáp án : D
Xét các trường hợp \({z_0}\) là số thực hoặc là số ảo.
Trường hợp \({z_0}\) là số thực, ta thay vào phương trình ban đầu tìm \(m.\)
Trường hợp \({z_0}\) là số ảo, ta sử dụng định lí Vi-ét đối với phương trình bậc hai ban đầu để tìm ra \(m.\)
TH1: \({z_0}\) là nghiệm thực \( \Rightarrow \left| {{z_0}} \right| = 6 \Leftrightarrow \left[ \begin{array}{l}{z_0} = 6\\{z_0} = - 6\end{array} \right.\)
Nếu \({z_0} = 6\) thay vào (*) ta có: \({6^2} - 12\left( {m + 1} \right) + {m^2} = 0 \Rightarrow {m^2} - 12m + 24 = 0 \Rightarrow m = 6 \pm 2\sqrt 3 \)
Nếu \({z_0} = - 6\) thay vào (*) ta có: \({\left( { - 6} \right)^2} + 12\left( {m + 1} \right) + {m^2} = 0 \Rightarrow {m^2} + 12m + 48 = 0\) (vô nghiệm)
TH2: \({z_0}\) là số phức \( \Leftrightarrow \Delta ' = {\left( {m + 1} \right)^2} - {m^2} = 2m + 1 < 0 \Leftrightarrow m < - \dfrac{1}{2}\)
Do đó phương trình có hai nghiệm phức \({z_0}\) và \(\overline {{z_0}} \).
Theo định lí Vi-ét ta có: \({z_0}.\overline {{z_0}} = {m^2}\)
Mà \(\left| {{z_0}} \right| = 6 \Rightarrow {\left| {{z_0}} \right|^2} = 36 \Rightarrow {z_0}.\overline {{z_0}} = 36\)
Suy ra \({m^2} = 36 \Rightarrow \left[ \begin{array}{l}m = 6\,\,\,\,(ktmdk)\\m = - 6\,(tmdk)\end{array} \right.\)
Vậy có \(3\) giá trị \(m\) thỏa mãn.
Đề thi THPT QG – 2021 lần 1– mã 104
Cho khối hộp chữ nhật \(ABCD.A'B'C'D'\) có đáy là hình vuông, \(BD = 4a\), góc giữa hai mặt phẳng \(\left( {A'BD} \right)\) và \(\left( {ABCD} \right)\) bằng \({60^o}\). Thể tích của khối hộp chữ nhật đã cho bằng
-
A.
\(48\sqrt 3 {a^3}\)
-
B.
\(\dfrac{{16\sqrt 3 }}{9}{a^3}\)
-
C.
\(\dfrac{{16\sqrt 3 }}{3}{a^3}\)
-
D.
\(16\sqrt 3 {a^3}\)
Đáp án : D
Áp dụng công thức
Xác định góc giữa hai mặt phẳng \(\left( {A'BD} \right)\) và \(\left( {ABCD} \right)\).
Sử dụng lượng giác trong tam giác vuông để tính chiều cao của khối hộp chữ nhật.
Tính thể tích khối hộp \(V = {S_d}.h\)
Gọi \(O\) là giao điểm của \(AC\) và \(BD.\)
Ta có: \(\left\{ \begin{array}{l}AO \bot BD\\AA' \bot BD\end{array} \right. \Rightarrow A'O \bot BD \Rightarrow\) Góc giữa hai mặt phẳng \(\left( {A'BD} \right)\) và \(\left( {ABCD} \right)\) là góc giữa A'O và AO và bằng \( \angle AOA' = {60^o}\)
Đáy \(ABCD\) là hình vuông có \(BD = 4a \Rightarrow AB = AD = 2a\sqrt 2 \)
Ta có: \(AO = \dfrac{1}{2}AC = \dfrac{1}{2}BD = 2a.\)
Trong \(\Delta AOA'\) có \(AA' = AO.\tan {60^o} = 2a\sqrt 3 \)
Vậy thể tích khối hộp \(ABCD.A'B'C'D'\) là: \(V = 8{a^2}.2a\sqrt 3 = 16{a^3}\sqrt 3 \)
Đề thi THPT QG – 2021 lần 1– mã 104
Cho hàm số \(f\left( x \right) = {x^3} + a{x^2} + bx + c\) với \(a,b,c\) là các số thực. Biết hàm số \(g\left( x \right) = f\left( x \right) + f'\left( x \right) + f''\left( x \right)\) có hai giá trị cực trị là \( - 5\) và \(2.\) Diện tích hình phẳng giới hạn bởi các đường \(y = \dfrac{{f\left( x \right)}}{{g\left( x \right) + 6}}\) và \(y = 1\) bằng
-
A.
\(\ln 3\)
-
B.
\(3\ln 2\)
-
C.
\(\ln 10\)
-
D.
\(\ln 7\)
Đáp án : B
Xét phương trình \(g'\left( x \right) = 0\) để suy ra hai nghiệm \(g\left( m \right) = - 5\) và \(g\left( n \right) = 2\)
Áp dụng công thức tính diện tích hình phẳng với hai cận \(x = m\) và \(x = n\)
Xét hàm số \(g\left( x \right) = f\left( x \right) + f'\left( x \right) + f''\left( x \right)\)
Ta có: \(g'\left( x \right) = f'\left( x \right) + f''\left( x \right) + f'''\left( x \right) = f'\left( x \right) + f''\left( x \right) + 6\)
Theo giả thiết ta có phương trình \(g'\left( x \right) = 0\) có hai nghiệm \(m,n\) và \(\left\{ \begin{array}{l}g\left( m \right) = - 5\\g\left( n \right) = 2\end{array} \right.\)
Xét phương trình \(\dfrac{{f\left( x \right)}}{{g\left( x \right) + 6}} = 1 \Rightarrow g\left( x \right) + 6 - f\left( x \right) = 0 \Leftrightarrow f'\left( x \right) + f''\left( x \right) + 6 = 0 \Leftrightarrow \left[ \begin{array}{l}x = m\\x = n\end{array} \right.\)
Diện tích hình phẳng cần tính là:
\(\left| {\int\limits_m^n {\left( {1 - \dfrac{{f\left( x \right)}}{{g\left( x \right) + 6}}} \right)dx} } \right| = \left| {\int\limits_m^n {\dfrac{{g\left( x \right) + 6 - f\left( x \right)}}{{g\left( x \right) + 6}}dx} } \right| = \left| {\int\limits_m^n {\dfrac{{f'\left( x \right) + f''\left( x \right) + 6}}{{g\left( x \right) + 6}}dx} } \right|\) \( = \left| {\int\limits_m^n {\dfrac{{g'\left( x \right)}}{{g\left( x \right) + 6}}dx} } \right|\)
\( = \left| {\ln \left| {g\left( x \right) + 6} \right|_m^n} \right| = \left| {\ln \left| {g\left( n \right) + 6} \right| - \ln \left| {g\left( m \right) + 6} \right|} \right| = \left| {\ln 8 - \ln 1} \right| = 3\ln 2.\)
Đề thi THPT QG – 2021 lần 1– mã 104
Xét các số phức \(z,{\rm{w}}\) thỏa mãn \(\left| z \right| = 1\) và \(\left| {\rm{w}} \right| = 2.\) Khi \(\left| {z + i\overline {\rm{w}} + 6 + 8i} \right|\) đạt giá trị nhỏ nhất, \(\left| {z - {\rm{w}}} \right|\) bằng
-
A.
\(\dfrac{{\sqrt {29} }}{5}\)
-
B.
\(\dfrac{{\sqrt {221} }}{5}\)
-
C.
\(3\) D. \(\sqrt 5 \)
-
D.
\(\sqrt 5 \)
Đáp án : A
Dùng phương pháp hình học \( \to \) kĩ năng dồn số phức.
Vẽ hình, lập luận để tìm ra giá trị \(\left| {z - {\rm{w}}} \right|\).
Gọi \(M\) và \(N\) lần lượt là các điểm biểu diễn số phức \(z + 6 + 8i\) và \(i\overline {\rm{w}} \).
Ta có: \(\left| z \right| = 1 \Leftrightarrow \left| {\left( {z + 6 + 8i} \right) + \left( { - 6 - 8i} \right)} \right| = 1 \Leftrightarrow MI = 1\) với \(I\left( { - 6; - 8} \right).\)
Suy ra tập hợp điểm \(M\) là đường tròn \(\left( {{T_1}} \right)\) tâm \(I\left( {6;8} \right)\) và bán kính \({R_1} = 1\).
Ta có: \(\left| {i\overline {\rm{w}} } \right| = \left| i \right|.\left| {\overline {\rm{w}} } \right| = 2.\)
Suy ra tập hợp điểm \(N\) là đường tròn \(\left( {{T_2}} \right)\) tâm \(O\) và bán kính \({R_2} = 2\).
Ta có: \(P = \left| {z + \overline {iw} + 6 + 8i} \right| = MN\)
\( \Rightarrow \min P = OI - {R_1} - {R_2} = 10 - 1 - 2 = 7\) (do \(\left( {{T_1}} \right)\) và \(\left( {{T_2}} \right)\) rời nhau).
Ta có: \(\left\{ \begin{array}{l}\overrightarrow {OM} = \dfrac{9}{{10}}\overrightarrow {OI} \\\overrightarrow {ON} = \dfrac{1}{5}\overrightarrow {OI} \end{array} \right. \Rightarrow \left\{ \begin{array}{l}M\left( { - \dfrac{{27}}{5}; - \dfrac{{36}}{5}} \right)\\N\left( { - \dfrac{6}{5}; - \dfrac{8}{5}} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}z = \dfrac{3}{5} + \dfrac{4}{5}i\\{\rm{w}} = \dfrac{8}{5} + \dfrac{6}{5}i\end{array} \right.\)
Vậy \(\left| {z - {\rm{w}}} \right| = \left| {\dfrac{3}{5} + \dfrac{4}{5}i - \dfrac{8}{5} - \dfrac{6}{5}i} \right| = \dfrac{{\sqrt {29} }}{5}\)
Đề thi THPT QG – 2021 lần 1– mã 104
Trong không gian \(Oxyz,\) cho hai điểm \(A\left( { - 2;1; - 3} \right)\) và \(B\left( {1; - 3;2} \right)\). Xét hai điểm \(M\) và \(N\) thay đổi thuộc mặt phẳng \(\left( {Oxy} \right)\) sao cho \(MN = 3.\) Giá trị lớn nhất của \(\left| {AM - BN} \right|\) bằng
-
A.
\(\sqrt {65} \)
-
B.
\(\sqrt {29} \)
-
C.
\(\sqrt {26} \)
-
D.
\(\sqrt {91} \)
Đáp án : A
Chỉ ra \(A\) và \(B\) nằm khác phía so với mặt phẳng \(\left( {Oxy} \right).\)
Lấy \(A'\) là điểm đối xứng của \(A\) qua \(\left( {Oxy} \right).\)
Từ đó lập luận, biến đổi để tìm được giá trị lớn nhất của \(P = \left| {AM - BN} \right|\).
Ta thấy \({z_A}.{z_B} < 0\) nên \(A,B\) nằm khác phía so với mặt phẳng \(\left( {Oxy} \right).\)
Gọi \(A'\) là điểm đối xứng với \(A\) qua \(\left( {Oxy} \right)\)\( \Rightarrow A'\left( { - 2;1;3} \right)\).
Gọi \(H\) là hình chiếu của \(A'\) trên \(\left( {Oxy} \right) \Rightarrow H\left( { - 2;1;0} \right)\)
Gọi \(I\) là hình chiếu của \(B\) trên \(\left( {Oxy} \right) \Rightarrow I\left( {1; - 3;0} \right)\)
Suy ra \(HI = 5\)
Khi đó \(P = \left| {AM - BN} \right| = \left| {A'M - BN} \right|\) \(\left( 1 \right)\)
Gọi \({A_1}\) là điểm sao cho \(\overrightarrow {{A_1}A'} = \overrightarrow {NM} \)
Do \(MN = 3\) nên \({A_1}\) thuộc đường tròn \(\left( C \right)\) tâm \(A'\) bán kính bằng \(3.\)
Khi đó \({A_1}A'MN\) là hình bình hành \( \Rightarrow A'M = {A_1}N\) \(\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) ta suy ra \(P \le {A_1}B\)
\( \Rightarrow {P_{\max }} = {A_1}B\) khi \({A_1},B,N\) thẳng hàng với \(N\) là giao điểm của \({A_1}B\) và \(\left( {Oxy} \right)\)
Khi đó \({A_1}B\) có giá trị lớn nhất khi \({A_1}\) thuộc đường tròn \(\left( C \right)\) tâm \(A'\) bán kính bằng \(3.\)
\({P_{\max }} = {A_1}B\) max \( = \sqrt {K{B^2} + {A_1}{K^2}} \)
Ta có: \(\left\{ \begin{array}{l}A'H = 3\\d\left( {B,\left( {Oxy} \right)} \right) = 2\end{array} \right. \Rightarrow BK = 1\)
Và \({A_1}K = A'{A_1} + A'K = {A_1}B' + HI = 3 + 5 = 8\)
\( \Rightarrow {P_{\max }} = \sqrt {{1^2} + {8^2}} = \sqrt {65} \)
Đề thi THPT QG – 2021 lần 1– mã 104
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = \left( {x - 9} \right)\left( {{x^2} - 16} \right),\,\forall x \in \mathbb{R}.\) Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số \(g\left( x \right) = f\left( {\left| {{x^3} + 7x} \right| + m} \right)\) có ít nhất \(3\) điểm cực trị?
-
A.
\(16\)
-
B.
\(9\)
-
C.
\(4\)
-
D.
\(8\)
Đáp án : D
Lập bảng biến thiên của hàm số \(h\left( x \right) = \left| {{x^3} + 7x} \right|\)
Tính đạo hàm \(g'\left( x \right)\) và tìm nghiệm của phương trình \(g'\left( x \right) = 0\)
Từ đó tìm mối liên hệ về tương giao giữa đồ thị hàm số \(f'\left( x \right),\,g'\left( x \right)\) và \(h'\left( x \right)\) để tìm được số giá trị \(m\) thỏa mãn.
Bảng biến thiên của \(h\left( x \right) = \left| {{x^3} + 7x} \right|\)
Xét \(g\left( x \right) = f\left( {\left| {{x^3} + 7x} \right| + m} \right)\). Ta có: \(g'\left( x \right) = \left( {\left| {{x^3} + 7x} \right|} \right)'.f'\left( {\left| {{x^3} + 7x} \right| + m} \right) = \left( {h\left( x \right)} \right)'.f'\left( {\left| {{x^3} + 7x} \right| + m} \right)\)
\(g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}h'\left( x \right) = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\f'\left( {\left| {{x^3} + 7x} \right| + m} \right) = 0\,\,\,\,\,\left( 2 \right)\end{array} \right.\)
Từ BBT của \(h\left( x \right) \Rightarrow h'\left( x \right) = 0\) chỉ chứa \(1\) nghiệm \(x = 0\) là điểm cực trị của \(h\left( x \right).\)
Do đó phương trình \(\left( 1 \right)\) có \(x = 0\) là nghiệm bội lẻ.
\(f'\left( x \right) = \left( {x - 9} \right)\left( {{x^2} - 16} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 9\\x = 4\\x = - 4\end{array} \right.\)
Phương trình \(\left( 2 \right)\) \( \Leftrightarrow \left[ \begin{array}{l}\left| {{x^3} + 7x} \right| + m = 9\\\left| {{x^3} + 7x} \right| + m = - 4\\\left| {{x^3} + 7x} \right| + m = 4\end{array} \right.\)
Ta có bảng biến thiên:
Để hàm số \(g\left( x \right)\) có ít nhất \(3\) điểm cực trị thì ít nhất \(1\) trong \(3\) đường thẳng \(y = 9,\,y = 4,\,y = - 4\) phải cắt \(\left( {\left| {{x^3} + 7x} \right| + m} \right)\) tại \(2\) điểm phân biệt (\(2\) nghiệm bội lẻ khác \(0\)).
\( \Leftrightarrow m < 9\). Có tất cả \(8\) giá trị nguyên dương \(m\) thỏa mãn.
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM; 70+ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
