Đề thi toán 9, đề kiểm tra toán 9 có đáp án và lời giải chi tiết

Đề kiểm tra học kì 2 Toán 9 - Đề số 1

Tổng hợp đề thi học kì 2 lớp 9 tất cả các môn

Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa - GDCD

Làm đề thi

Đề bài

Câu 1 :

Cho $\Delta ABC$ cân tại $A$ có $\widehat {BAC} = {120^0}.$ Trên nửa mặt phẳng bờ $BC$ không chứa đỉnh $A$, lấy $D$ sao cho $BCD$ là tam giác đều. Khi đó

A.

$\Delta ACD$ cân
B.

$ABDC$ nội tiếp
C.

$ABDC$ là hình thang
D.

$ABDC$ là hình vuông

Câu 2 :

Mỗi một tam giác có bao nhiêu đường tròn bàng tiếp?

A.

$1$
B.

$2$
C.

$3$
D.

$4$

Câu 3 :

Chọn phát biểu đúng. Phương trình $a{x^2} + bx + c = 0\,\,(a \ne 0)$ có hai nghiệm ${x_1};{x_2}$. Khi đó

A.

$\left\{ \begin{array}{l}{x_1} + {x_2} = - \dfrac{b}{a}\\{x_1}.{x_2} = \dfrac{c}{a}\end{array} \right.$
B.

$\left\{ \begin{array}{l}{x_1} + {x_2} = \dfrac{b}{a}\\{x_1}.{x_2} = \dfrac{c}{a}\end{array} \right.$
C.

$\left\{ \begin{array}{l}{x_1} + {x_2} = - \dfrac{b}{a}\\{x_1}.{x_2} = - \dfrac{c}{a}\end{array} \right.$
D.

$\left\{ \begin{array}{l}{x_1} + {x_2} = \dfrac{b}{a}\\{x_1}.{x_2} = - \dfrac{c}{a}\end{array} \right.$

Câu 4 :

Số giao điểm của đường thẳng $d:y = 2x + 4$ và parabol $\left( P \right):y = {x^2}$ là:

A.

$2$
B.

$1$
C.

$0$
D.

$3$

Câu 5 :

“Đồ thị hàm số $y = {\rm{ax}} + b\,(a \ne 0)$ cắt trục hoành tại điểm có hoành độ bằng ... và cắt trục tung tại điểm có tung độ bằng ...” . Trong dấu “…” lần lượt là?

A.

$\dfrac{b}{a};b$
B.

$\dfrac{{ - b}}{a};b$
C.

$\dfrac{b}{a}; - b$
D.

$ - \dfrac{b}{a}; - b$

Câu 6 :

Cho $3$ điểm $A(0;3),B(2;2);C(m + 3;m)$. Giá trị của $m$ để $3$ điểm $A,B,C$ thẳng hàng là:

A.

$1$
B.

$ - 3$
C.

$3$
D.

$ - 1$

Câu 7 :

Đường tròn là hình:

A.

Không có trục đối xứng
B.

Có một trục đối xứng
C.

Có hai trục đối xứng
D.

Có vô số trục đối xứng

Câu 8 :

Cho hệ phương trình $\left\{ \begin{array}{l}x - y = 5\\3x + 2y = 18\end{array} \right.$có nghiệm $\left( {x;y} \right)$. Tích $x.y$ là

A.

$5$
B.

$\dfrac{84}{25}$
C.

$\dfrac{25}{84}$
D.

$\dfrac{84}{5}$

Câu 9 :

Cho $3$ đường thẳng $\left( d \right):{\rm{ }}y = \left( {m + 2} \right)x - 3m;\left( {d'} \right):{\rm{ }}y = 2x + 4\;;\left( {d''} \right):{\rm{ }}y = - 3x - 1.$ Giá trị của $m$ để $3$ đường thẳng trên đồng quy là :

A.

$ - 1$
B.

$1$
C.

$2$
D.

$ - 2$

Câu 10 :

Phương trình $\sqrt {x - 5} = \sqrt {3 - x} {\rm{ }}$ có bao nhiêu nghiệm?

A.

$1$
B.

$0$
C.

$2$
D.

$3$

Câu 11 :

Không giải phương trình, tính tổng hai nghiệm (nếu có) của phương trình ${x^2} - 6x + 7 = 0$

A.

$\dfrac{1}{6}$
B.

$3$
C.

$6$
D.

$7$

Câu 12 :

Cho hai đường tròn $\left( {O;8\,cm} \right)$ và $\left( {O';6cm} \right)$ cắt nhau tại $A,B$ sao cho $OA$ là tiếp tuyến của $\left( {O'} \right)$. Độ dài dây $AB$ là

A.

$AB = 8,6\,cm$
B.

$AB = 6,9\,cm$
C.

$AB = 4,8\,cm$
D.

$AB = 9,6\,cm$

Câu 13 :

Cho $B = \dfrac{2}{{\sqrt 2 }} + \dfrac{1}{{\sqrt 3 - \sqrt 2 }} - \dfrac{2}{{\sqrt 3 - 1}}$ và $C = \left( {2\sqrt 3 - 5\sqrt {27} + 4\sqrt {12} } \right):\sqrt 3 $. Chọn đáp án đúng.

A.

$B > C$
B.

$B < C$
C.

$B = C$
D.

$B = - C$

Câu 14 :

Cho nửa đường tròn $\left( O \right)$ đường kính $AB$ và $C$ là điểm trên cung nhỏ $AB$ (cung $CB$ nhỏ hơn cung $CA$ ). Tiếp tuyến tại $C$ của nửa đường tròn cắt đường thẳng $AB$ tại $D$ . Biết tam giác $ADC$ cân tại $C$ . Tính góc $ADC$ .

A.

$40^\circ $
B.

$45^\circ $
C.

$60^\circ $
D.

$30^\circ $

Câu 15 :

Giải phương trình $\sqrt {2{x^2} - 4x + 5} = x - 2$ ta được nghiệm là

A.

$x = 1$
B.

$x = 3$
C.

$x = 2$
D.

Phương trình vô nghiệm

Câu 16 :

Đường thẳng $y = a{\rm{x}} + b$ đi qua $2$ điểm $M\left( { - 3;2} \right)$ và $N\left( {1; - 1} \right)$ là:

A.

$y = - \dfrac{3}{4}x + \dfrac{1}{4}$
B.

$y = - \dfrac{3}{4}x - \dfrac{1}{4}$
C.

$y = - \dfrac{2}{3}x + \dfrac{1}{4}$
D.

$y = - \dfrac{3}{4}x + 1$

Câu 17 :

Cho hai đường thẳng:

${d_1}:mx - 2\left( {3n + 2} \right)y = 6$ và ${d_2}:\left( {3m - 1} \right)x + 2ny = 56.$

Tìm tích $m. n$ để hai đường thẳng cắt nhau tại điểm $I\left( { - 2;3} \right)$.

A.

$0$
B.

$1$
C.

$2$
D.

$ - 2$

Câu 18 :

Cho hệ phương trình $\left\{ \begin{array}{l}2x + by = - 1\\bx - 2ay = 1\end{array} \right.$. Biết rằng hệ phương trình có nghiệm là $\left( {1; - 2} \right)$, tính $a - b$.

A.

$\dfrac{{13}}{8}$
B.

$ - \dfrac{{13}}{8}$
C.

$\dfrac{5}{8}$
D.

$ - \dfrac{5}{8}$

Câu 19 :

Cho hệ phương trình $\left\{ \begin{array}{l}4\sqrt x - 3\sqrt y = 4\\2\sqrt x + \sqrt y = 2\end{array} \right.$. Biết nghiệm của hệ phương trình là $\left( {x;y} \right)$, tính $x.y$

A.

$2$
B.

$0$
C.

$-2$
D.

$1$

Câu 20 :

Số nghiệm của hệ phương trình $\left\{ \begin{array}{l}5(x + 2y) - 3(x - y) = 99\\x - 3y = 7x - 4y - 17\end{array} \right.$là

A.

$2$
B.

Vô số
C.

$1$
D.

$0$

Câu 21 :

Cho hệ phương trình $\left\{ \begin{array}{l}(m - 1)x + y = 2\\mx + y = m + 1\end{array} \right.$ ($m$ là tham số). Kết luận nào sau đây là đúng khi nói về nghiệm $\left( {x;y} \right)$ của hệ phương trình

A.

Hệ phương trình luôn có nghiệm duy nhất $\left( {x;y} \right)$ thỏa mãn $2x + y \le {\rm{3}}$
B.

Hệ phương trình luôn có nghiệm duy nhất $\left( {x;y} \right)$ thỏa mãn $2x + y > {\rm{3}}$
C.

Hệ phương trình luôn có nghiệm duy nhất $\left( {x;y} \right)$ thỏa mãn $2x + y \ge {\rm{3}}$
D.

Hệ phương trình luôn có nghiệm duy nhất $\left( {x;y} \right)$ thỏa mãn $2x + y = {\rm{3}}$

Câu 22 :

Hai vòi nước cùng chảy vào một bể thì sau $4$ giờ $48$ phút bể đầy. Nếu vòi I chảy riêng trong $4$ giờ, vòi II chảy riêng trong $3$ giờ thì cả hai vòi chảy được $\dfrac{3}{4}$ bể. Tính thời gian vòi I một mình đầy bể.

A.

$6$ giờ
B.

$8$ giờ
C.

$10$ giờ
D.

$12$ giờ

Câu 23 :

Hai xí nghiệp theo kế hoạch phải làm tổng cộng $360$ dụng cụ. Trên thực tế, xí nghiệp $1$ vượt mức $12\% $ , xí nghiệp $2$ vượt mức $10\% $ , do đó cả hai xí nghiệp làm tổng cộng $400$ dụng cụ. Tính số dụng cụ xí nghiệp $2$ phải làm theo kế hoạch

A.

$160$ dụng cụ
B.

$200$ dụng cụ.
C.

$120$ dụng cụ.
D.

$240$ dụng cụ.

Câu 24 :

Tìm các giá trị của $m$ để phương trình $m{x^2} - 2\left( {m - 2} \right)x + 3\left( {m - 2} \right) = 0$ có hai nghiệm phân biệt cùng dấu.

A.

$m < 0$
B.

$m > 1$
C.

$ - 1 < m < 0$
D.

$m > 0$

Câu 25 :

Tìm hai nghiệm của phương trình $18{x^2} + 23x + 5 = 0$ sau đó phân tích đa thức $A = 18{x^2} + 23x + 5$ sau thành nhân tử.

A.

${x_1} = - 1;{x_2} = - \dfrac{5}{{18}};$

$A = 18\left( {x + 1} \right)\left( {x + \dfrac{5}{{18}}} \right)$
B.

${x_1} = - 1;{x_2} = - \dfrac{5}{{18}};$

$A = \left( {x + 1} \right)\left( {x + \dfrac{5}{{18}}} \right)$
C.

${x_1} = - 1;{x_2} = \dfrac{5}{{18}};$

$A = 18\left( {x + 1} \right)\left( {x - \dfrac{5}{{18}}} \right)$
D.

${x_1} = 1;{x_2} = - \dfrac{5}{{18}};$

$A = 18\left( {x - 1} \right)\left( {x + \dfrac{5}{{18}}} \right)$

Câu 26 :

Phương trình $\left( {\dfrac{{1 + x}}{{1 - x}} - \dfrac{{1 - x}}{{1 + x}}} \right):\left( {\dfrac{{1 + x}}{{1 - x}} - 1} \right) = \dfrac{3}{{14 - x}}$ có nghiệm là:

A.

$x = \sqrt 2 $
B.

$x = 2$
C.

$x = 3$
D.

$x = 5$

Câu 27 :

Phương trình $\dfrac{{2x}}{{x - 2}} - \dfrac{5}{{x - 3}} = \dfrac{{ - 9}}{{{x^2} - 5x + 6}}$có số nghiệm là

A.

$2$
B.

$1$
C.

$0$
D.

$3$

Câu 28 :

Tìm tham số $m$ để đường thẳng $d:y = mx + 2$ cắt parabol $\left( P \right):y = \dfrac{{{x^2}}}{2}$ tại hai điểm phân biệt

A.

$m = 2$
B.

$m = - 2$
C.

$m = 4$
D.

$m \in \mathbb{R}$

Câu 29 :

Cho đường tròn $(O;R)$. Cát tuyến qua $A$ ở ngoài $(O)$ cắt $(O)$ tại $B$ và $C$. Cho biết $AB = BC$ và kẻ đường kính $COD$. Tính độ dài đoạn thẳng $AD.$

A.

$AD = R$
B.

$AD = 3R$
C.

$AD = \dfrac{R}{2}$
D.

$AD = 2R$

Câu 30 :

Hai tiếp tuyến tại $A$ và $B$ của đường tròn $(O)$ cắt nhau tại $I$ . Đường thẳng qua $I$ và vuông góc với $IA$ cắt $OB$ tại $K$. Chọn khẳng định đúng.

A.

$OI = OK = KI$
B.

$KI = KO$
C.

$OI = OK$
D.

$IO = IK$

Câu 31 :

Hai tiếp tuyến tại $A$ và $B$ của đường tròn $\left( {O;R} \right)$ cắt nhau tại $M.$ Nếu $MA = \;R\sqrt 3 $ thì góc $\widehat {AOB}$ bằng:

A.

${120^0}\;$
B.

${90^0}$
C.

${60^0}$
D.

${45^0}$

Câu 32 :

Cho tam giác $ABC$ nội tiếp đường tròn $(O;R),$đường cao $AH,$ biết $AB = 9{\rm{ }}cm,$ $AC = 12{\rm{ }}cm,$ $AH = 4{\rm{ }}cm.$ Tính bán kính của đường tròn $(O)$.

A.

$13,5\,cm$
B.

$12\,cm$
C.

$18\,cm$
D.

$6\,cm$

Câu 33 :

Cho đường tròn $(O)$ và hai dây cung $AB,AC$ bằng nhau. Qua $A$ vẽ một cát tuyến cắt dây $BC$ ở $D$ và cắt $(O)$ ở $E$. Khi đó $A{B^2}$ bằng

A.

$AD.AE$
B.

$AD.AC$
C.

$AE.BE$
D.

$AD.BD$

Câu 34 :

Cho nửa đường tròn $(O)$ đường kính $AB$ và một điểm $C$ trên nửa đường tròn. Gọi $D$ là một điểm trên đường kính $AB$; qua $D$ kẻ đường vuông góc với $AB$ cắt $BC$ tại $F$, cắt $AC$ tại $E$. Tiếp tuyến của nửa đường tròn tại $C$cắt $EF$ tại $I.$Khi đó

A.

$IE = IF$
B.

$IE = 2IF$
C.

$EF = 3IE$
D.

$EF = 3IF$

Câu 35 :

Cho tam giác nhọn $ABC$ nội tiếp $\left( O \right)$ . Kẻ tiếp tuyến $xAy$ với $\left( O \right)$ . Từ $B$ kẻ $BM{\rm{//}}xy\left( {M \in AC} \right)$ . Khi đó tích $AM.AC$ bằng

A.

$A{B^2}$
B.

$B{C^2}$
C.

$A{C^2}$
D.

$A{M^2}$

Câu 36 :

Cho $\Delta ABC$ vuông ở $A$ . Trên cạnh $AC$ lấy điểm $M$ và vẽ đường tròn đường kính $MC$ . Kẻ $BM$ cắt đường tròn tại $D$ . Đường thẳng $DA$ cắt đường tròn tại $S$ . Chọn đáp án sai trong các đáp án sau:

A.

Tứ giác $ABCD$ nội tiếp.
B.

$\widehat {ABD} = \widehat {ACD}$
C.

$CA$ là phân giác của $\widehat {SCB}.$
D.

Tứ giác $ABCS$ nội tiếp.

Câu 37 :

Cho nửa $(O)$ đường kính $AB.$ Lấy $M \in OA(M \ne O,A).$ Qua $M$ vẽ đường thẳng $d$ vuông góc với $AB.$ Trên $d$ lấy $N$ sao cho $ON > R.$ Nối $NB$ cắt $(O)$ tại $C.$ Kẻ tiếp tuyến $NE$ với $(O)$ ($E$ là tiếp điểm, $E$ và $A$ cùng thuộc nửa mặt phẳng bờ $d$). Gọi $H$ là giao điểm của $AC$ và $d$, $F$ là giao điểm của $EH$ và đường tròn $(O)$. Chọn khẳng định sai?

A.

Bốn điểm $O,E,M,N$ cùng thuộc một đường tròn
B.

$N{E^2} = NC.NB$
C.

$\widehat {NEH} = \widehat {NME}$
D.

$\widehat {NFO} < 90^\circ $

Câu 38 :

Cho $A = \dfrac{{2x}}{{x + 3\sqrt x + 2}} + \dfrac{{5\sqrt x + 1}}{{x + 4\sqrt x + 3}} + \dfrac{{\sqrt x + 10}}{{x + 5\sqrt x + 6}}$ với $x \ge 0$. Chọn đáp án đúng.

A.

$A = 2\sqrt x $
B.

Giá trị của $A$ không phụ thuộc vào biến $x.$
C.

$A = 3\left( {\sqrt x + 2} \right)$
D.

$A = \dfrac{2}{{\sqrt x + 1}}$

Câu 39 :

Cho đường thẳng $d:y = x + 2;d':y = - 2x + 5$. Gọi $M$ là giao điểm của $d$ và $d'$ . $A$ và $B$ lần lượt là giao điểm của $d$ và $d'$ với trục hoành. Khi đó diện tích tam giác $AMB$ là:

A.

$\dfrac{{27}}{6}$ ( đvdt)
B.

$27$( đvdt)
C.

$\dfrac{{27}}{2}$ (đvdt)
D.

$\dfrac{{27}}{4}$(đvdt)

Câu 40 :

Cho $A$ là điểm cố định trên đường tròn $\left( {O;R} \right).$ Gọi $AB$ và $AC$ là hai dây cung thay đổi trên đường tròn $\left( O \right)$ thỏa mãn $\sqrt {AB.AC} = R\sqrt 3 .$ Khi đó vị trí của $B,\,C$ trên $\left( O \right)$ để diện tích $\Delta ABC$ lớn nhất là:

A.

$\Delta ABC$ cân
B.

$\Delta ABC$ đều.
C.

$\Delta ABC$ vuông cân
D.

$\Delta ABC$ vuông

Lời giải và đáp án

Câu 1 :

Cho $\Delta ABC$ cân tại $A$ có $\widehat {BAC} = {120^0}.$ Trên nửa mặt phẳng bờ $BC$ không chứa đỉnh $A$, lấy $D$ sao cho $BCD$ là tam giác đều. Khi đó

A.

$\Delta ACD$ cân
B.

$ABDC$ nội tiếp
C.

$ABDC$ là hình thang
D.

$ABDC$ là hình vuông

Đáp án : B

Phương pháp giải :

Tứ giác có tổng hai góc đối bằng ${180^0}$ là tứ giác nội tiếp.

Lời giải chi tiết :

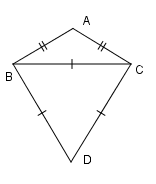
Ta có $\Delta BCD$ là tam giác đều nên $\widehat {DCB} = {60^0}\,\,\left( 1 \right).$ Mặt khác $\Delta ABC$ là tam giác cân tại $A$ có $\widehat {BAC} = {120^0}$ hơn nữa tổng ba góc trong một tam giác bằng ${180^0}$ nên ta nhận được

$\left\{ \begin{array}{l}\widehat {ACB} = \widehat {ABC}\\\widehat {ACB} + \widehat {ABC} + \widehat {BAC} = {180^0}\end{array} \right. \Rightarrow \widehat {ACB} = {30^0}\,\,\,\,\left( 2 \right)$ .

Từ $\left( 1 \right)$ và $\left( 2 \right)$ ta có $\widehat {DCA} = \widehat {DCB} + \widehat {BCA} = {60^0} + {30^0} = {90^0}\,\,\left( 3 \right)$.

Chứng minh tương tự ta có $\widehat {ABD} = {90^0}\,\,\left( 4 \right).$

Từ $\left( 3 \right)$ và $\left( 4 \right)$ ta nhận được $\widehat {ABD} + \widehat {DCA} = {90^0} + {90^0} = {180^0}\,.$

Vậy tứ giác $ABDC$ là tứ giác nội tiếp.

Câu 2 :

Mỗi một tam giác có bao nhiêu đường tròn bàng tiếp?

A.

$1$
B.

$2$
C.

$3$
D.

$4$

Đáp án : C

Lời giải chi tiết :

Đường tròn tiếp xúc với một cạnh của tam giác và tiếp xúc với phần kéo dàicủa hai cạnh còn lại gọi là đường tròn bàng tiếp tam giác.

Với một tam giác có ba đường tròn bàng tiếp.

Câu 3 :

Chọn phát biểu đúng. Phương trình $a{x^2} + bx + c = 0\,\,(a \ne 0)$ có hai nghiệm ${x_1};{x_2}$. Khi đó

A.

$\left\{ \begin{array}{l}{x_1} + {x_2} = - \dfrac{b}{a}\\{x_1}.{x_2} = \dfrac{c}{a}\end{array} \right.$
B.

$\left\{ \begin{array}{l}{x_1} + {x_2} = \dfrac{b}{a}\\{x_1}.{x_2} = \dfrac{c}{a}\end{array} \right.$
C.

$\left\{ \begin{array}{l}{x_1} + {x_2} = - \dfrac{b}{a}\\{x_1}.{x_2} = - \dfrac{c}{a}\end{array} \right.$
D.

$\left\{ \begin{array}{l}{x_1} + {x_2} = \dfrac{b}{a}\\{x_1}.{x_2} = - \dfrac{c}{a}\end{array} \right.$

Đáp án : A

Lời giải chi tiết :

Cho phương trình bậc hai $a{x^2} + bx + c = 0\,(a \ne 0).$ Nếu ${x_1},{x_2}$ là hai nghiệm của phương trình thì

$\left\{ \begin{array}{l}{x_1} + {x_2} = \dfrac{{ - b}}{a}\\{x_1} \cdot {x_2} = \dfrac{c}{a}\end{array} \right..$

Câu 4 :

Số giao điểm của đường thẳng $d:y = 2x + 4$ và parabol $\left( P \right):y = {x^2}$ là:

A.

$2$
B.

$1$
C.

$0$
D.

$3$

Đáp án : A

Phương pháp giải :

Bước 1: Giải phương trình hoành độ giao điểm.

Bước 2: Số nghiệm vừa tìm được của phương trình là số giao điểm của đường thẳng và parabol

Lời giải chi tiết :

Xét phương trình hoành độ giao điểm ${x^2} = 2x + 4 \Leftrightarrow {x^2} - 2x - 4 = 0$ có $\Delta ' = 5 > 0$ nên phương trình có hai nghiệm phân biệt hay đường thẳng cắt parabol tại hai điểm phân biệt.

Câu 5 :

A.

$\dfrac{b}{a};b$
B.

$\dfrac{{ - b}}{a};b$
C.

$\dfrac{b}{a}; - b$
D.

$ - \dfrac{b}{a}; - b$

Đáp án : B

Phương pháp giải :

- ĐTHS cắt trục hoành thì cho $y=0$ từ đó tìm được $x,$ ĐTHS cắt trục tung thì cho $x=0$ từ đó tìm được $y.$

- So sánh với đề bài để tìm ra biểu thức cần điền vào chỗ trống.

Lời giải chi tiết :

Đồ thị hàm số $y = {\rm{ax}} + b$ cắt trục hoành $ \Rightarrow y = 0 \Rightarrow {\rm{ax}} + b = 0 \Leftrightarrow x = - \dfrac{b}{a}$

ĐTHS $y = {\rm{ax}} + b$ cắt trục tung $ \Rightarrow x = 0 \Rightarrow y = {\rm{a}}{\rm{.0}} + b \Rightarrow y = b$

Vậy đồ thị hàm số $y = {\rm{ax}} + b\,(a \ne 0)$ cắt trục hoành tại điểm có hoành độ bằng $-\dfrac{b}{a}$ và cắt trục tung tại điểm có tung độ bằng $b$.

Câu 6 :

Cho $3$ điểm $A(0;3),B(2;2);C(m + 3;m)$. Giá trị của $m$ để $3$ điểm $A,B,C$ thẳng hàng là:

A.

$1$
B.

$ - 3$
C.

$3$
D.

$ - 1$

Đáp án : A

Phương pháp giải :

- Viết phương trình đường thẳng $(d)$ đi qua 2 điểm cho trước $A;B$.

- Để $3$ điểm $A;B;C$ thẳng hàng thì $C \in (d)$

Lời giải chi tiết :

Gọi $d:y = {\rm{ax}} + b$ là đường thẳng đi qua $A$ và $B$.

$\begin{array}{l}A(0;3) \in d \Leftrightarrow a.0 + b = 3 \Leftrightarrow b = 3\\B(2;2) \in d \Leftrightarrow a.2 + b = 2\\ \Rightarrow \left\{ \begin{array}{l}b = 3\\2a + b = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 3\\a = - \dfrac{1}{2}\end{array} \right. \Rightarrow d:y = - \dfrac{1}{2}x + 3\end{array}$

Để $3$ điểm $A,B,C$ thẳng hàng thì $C(m + 3;m) \in (d):y = - \dfrac{1}{2}x + 3$

$ \Leftrightarrow m = - \dfrac{1}{2}\left( {m + 3} \right) + 3 \Leftrightarrow \dfrac{3}{2}m = \dfrac{3}{2} \Leftrightarrow m = 1$.

Vậy $m = 1$.

Câu 7 :

Đường tròn là hình:

A.

Không có trục đối xứng
B.

Có một trục đối xứng
C.

Có hai trục đối xứng
D.

Có vô số trục đối xứng

Đáp án : D

Phương pháp giải :

Hình có trục đối xứng là hình khi lấy đối xứng hình đó qua trục đối xứng ta cũng được chính hình đó.

Lời giải chi tiết :

Đường tròn có trục đối xứng là đường thẳng đi qua tâm của nó. Do có vô số đường kính nên đường tròn có vô số trục đối xứng.

Câu 8 :

Cho hệ phương trình $\left\{ \begin{array}{l}x - y = 5\\3x + 2y = 18\end{array} \right.$có nghiệm $\left( {x;y} \right)$. Tích $x.y$ là

A.

$5$
B.

$\dfrac{84}{25}$
C.

$\dfrac{25}{84}$
D.

$\dfrac{84}{5}$

Đáp án : B

Lời giải chi tiết :

Ta có $\left\{ \begin{array}{l}x - y = 5\\3x + 2y = 18\end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l}x = y + 5\\3.\left( {y + 5} \right) + 2y = 18\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = y + 5\\3y + 15 + 2y = 18\end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l}x = y + 5\\5y = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = \dfrac{3}{5}\\x = 5 + \dfrac{3}{5}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{1}x = \dfrac{28}{5}\\y = \dfrac{3}{5}\end{array} \right.$

Vậy hệ phương trình có nghiệm duy nhất $\left( {x;y} \right) = \left( {\dfrac{28}{5};\dfrac{3}{5}} \right) \Rightarrow x.y = \dfrac{84}{25}$

Câu 9 :

A.

$ - 1$
B.

$1$
C.

$2$
D.

$ - 2$

Đáp án : A

Phương pháp giải :

- Tìm tọa độ giao điểm 2 đường thẳng cho trước $d';d''$

- Cho giao điểm vừa tìm được thuộc vào đường thẳng $d$.

Điểm $M\left( {{x_0};{y_0}} \right)$ thuộc đường thẳng $\left( d \right):y = ax + b $$\Leftrightarrow {y_0} = a{x_0} + b$

Lời giải chi tiết :

Xét phương trình hoành độ giao điểm $A$ của $\left( {d'} \right)$ và $\left( {d''} \right)$:

$\begin{array}{*{20}{l}}{2x + 4 = - 3x - 1}\\{ \Leftrightarrow 5x = - 5}\\{ \Leftrightarrow x = - 1}\\{ \Rightarrow y = 2\left( { - 1} \right) + 4 = 2}\\{ \Rightarrow A\left( { - 1;2} \right)}\end{array}$

Để $\left( d \right);\left( {d'} \right);\left( {d''} \right)$ đồng quy thì $A\left( { - 1;2} \right) \in \left( d \right)$

$\begin{array}{*{20}{l}}{ \Leftrightarrow 2 = \left( {m + 2} \right).\left( { - 1} \right) - 3m}\\{ \Leftrightarrow 2 = - 2 - 4m}\\{ \Leftrightarrow 4m = - 4}\\{ \Leftrightarrow m = - 1}\end{array}$

Vậy khi $m = - 1$ thì $\left( d \right);\left( {d'} \right);\left( {d''} \right)$ đồng quy tại $A\left( { - 1;2} \right)$.

Câu 10 :

Phương trình $\sqrt {x - 5} = \sqrt {3 - x} {\rm{ }}$ có bao nhiêu nghiệm?

A.

$1$
B.

$0$
C.

$2$
D.

$3$

Đáp án : B

Phương pháp giải :

Giải phương trình dạng $\sqrt A = \sqrt B $

ĐK: $A \ge 0$ (hoặc $B \ge 0$ )

Khi đó $\sqrt A = \sqrt B \Leftrightarrow A = B$

So sánh với điều kiện rồi kết luận.

Lời giải chi tiết :

Điều kiện: $x \ge 5$

Ta có $\sqrt {x - 5} = \sqrt {3 - x} {\rm{ }}$$ \Leftrightarrow x - 5 = 3 - x \Leftrightarrow x + x = 3 + 5 \Leftrightarrow 2x = 8 \Leftrightarrow x = 4\,\,\left( {KTM} \right)$

Vậy phương trình đã cho vô nghiệm.

Câu 11 :

Không giải phương trình, tính tổng hai nghiệm (nếu có) của phương trình ${x^2} - 6x + 7 = 0$

A.

$\dfrac{1}{6}$
B.

$3$
C.

$6$
D.

$7$

Đáp án : C

Phương pháp giải :

Sử dụng hệ thức Vi-et

Nếu ${x_1},{x_2}$ là hai nghiệm của phương trình $a{x^2} + bx + c = 0\,\,(a \ne 0)$ thì $\left\{ \begin{array}{l}{x_1} + {x_2} = \dfrac{{ - b}}{a}\\{x_1} \cdot {x_2} = \dfrac{c}{a}\end{array} \right..$

Lời giải chi tiết :

Phương trình ${x^2} - 6x + 7 = 0$ có $\Delta = {\left( { - 6} \right)^2} - 4.1.7 = 8 > 0$ nên phương trình có hai nghiệm ${x_1};{x_2}$

Theo hệ thức Vi-et ta có ${x_1} + {x_2} = - \dfrac{{ - 6}}{1} \Leftrightarrow {x_1} + {x_2} = 6$

Câu 12 :

Cho hai đường tròn $\left( {O;8\,cm} \right)$ và $\left( {O';6cm} \right)$ cắt nhau tại $A,B$ sao cho $OA$ là tiếp tuyến của $\left( {O'} \right)$. Độ dài dây $AB$ là

A.

$AB = 8,6\,cm$
B.

$AB = 6,9\,cm$
C.

$AB = 4,8\,cm$
D.

$AB = 9,6\,cm$

Đáp án : D

Phương pháp giải :

Sử dụng tính chất đường nối tâm của hai đường tròn cắt nhau và hệ thức lượng trong tam giác vuông.

Lời giải chi tiết :

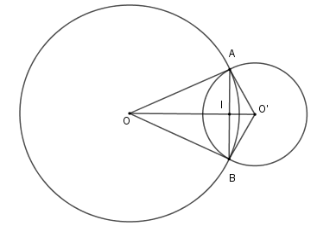
Vì $OA$ là tiếp tuyến của $\left( {O'} \right)$ nên $\Delta OAO'$ vuông tại $A$.

Vì $\left( O \right)$ và $\left( {O'} \right)$ cắt nhau tại $A,B$ nên đường nối tâm $OO'$ là trung trực của đoạn $AB$.

Gọi giao điểm của $AB$ và $OO'$ là $I$ thì $AB \bot OO'$ tại $I$ là trung điểm của $AB$

Áp dụng hệ thức lượng trong tam giác vuông $OAO'$ ta có

$\dfrac{1}{{A{I^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O'{A^2}}} = \dfrac{1}{{{8^2}}} + \dfrac{1}{{{6^2}}} \Rightarrow AI = 4,8\,cm \Rightarrow AB = 9,6\,cm$

Câu 13 :

A.

$B > C$
B.

$B < C$
C.

$B = C$
D.

$B = - C$

Đáp án : A

Phương pháp giải :

+ Tính $B;C$ bằng cách sử dụng các công thức

Với $A > 0$ và $A \ne {B^2}$ thì $\dfrac{C}{{\sqrt A \pm B}} = \dfrac{{C(\sqrt A \mp B)}}{{A - {B^2}}}$

Khai phương một tích: $\sqrt {A.B} = \sqrt A .\sqrt B {\rm{ }}(A \ge 0,B \ge 0)$

+ So sánh $B;C.$

Lời giải chi tiết :

Ta có $B = \dfrac{2}{{\sqrt 2 }} + \dfrac{1}{{\sqrt 3 - \sqrt 2 }} - \dfrac{2}{{\sqrt 3 - 1}}$

$ = \dfrac{{2\sqrt 2 }}{{\sqrt 2 .\sqrt 2 }} + \dfrac{{\sqrt 3 + \sqrt 2 }}{{\left( {\sqrt 3 - \sqrt 2 } \right)\left( {\sqrt 3 + \sqrt 2 } \right)}} - \dfrac{{2\left( {\sqrt 3 + 1} \right)}}{{\left( {\sqrt 3 - 1} \right)\left( {\sqrt 3 + 1} \right)}}$

$
= \dfrac{{2\sqrt 2 }}{2} + \dfrac{{\sqrt 3 + \sqrt 2 }}{{3 - 2}} - \dfrac{{2\left( {\sqrt 3 + 1} \right)}}{{3 - 1}}$
$= \sqrt 2 + \dfrac{{\sqrt 3 + \sqrt 2 }}{1} - \dfrac{{2\left( {\sqrt 3 + 1} \right)}}{2}$

$ = \sqrt 2 + \sqrt 3 + \sqrt 2 - \left( {\sqrt 3 + 1} \right)$

$ = \sqrt 2 + \sqrt 3 + \sqrt 2 - \sqrt 3 - 1$

$ = 2\sqrt 2 - 1$

Lại có

$\begin{array}{l}C = (2\sqrt 3 - 5\sqrt {27} + 4\sqrt {12} ):\sqrt 3 \\ = \left( {2\sqrt 3 - 5\sqrt {9.3} + 4\sqrt {4.3} } \right):\sqrt 3 \\= (2\sqrt 3 - 5.3\sqrt 3 + 4.2\sqrt 3 ):\sqrt 3 \\ = - 5\sqrt 3 :\sqrt 3 \\ = - 5\end{array}$

Nhận thấy $B = 2\sqrt 2 - 1 > 0;\,C = - 5 < 0 \Rightarrow B > C$

Câu 14 :

A.

$40^\circ $
B.

$45^\circ $
C.

$60^\circ $
D.

$30^\circ $

Đáp án : D

Phương pháp giải :

Sử dụng góc nội tiếp và góc có đỉnh bên ngoài đường tròn

Lời giải chi tiết :

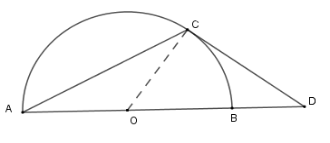
Xét nửa $\left( O \right)$ có $\widehat {BAC} = \dfrac{1}{2}$ sđ $\overparen{BC}$ (góc nội tiếp chắn cung BC) và $\widehat {CDA} = \dfrac{1}{2}$ (sđ $\overparen{AC} - $ sđ $\overparen{BC}$ ) (góc có đỉnh bên ngoài đường tròn)

Mà $\Delta ADC$ cân tại $C$ nên $\widehat {DAC} = \widehat {CDA} \Leftrightarrow $ sđ $\overparen{BC} = $ sđ $\overparen{AC} - $ sđ $\overparen{BC}$

Suy ra sđ $\overparen{AC} = 2$. sđ $\overparen{BC}$

Mà sđ $\overparen{AC} + $ sđ $\overparen{BC} = 180^\circ $ nên sđ $\overparen{AC} = 120^\circ $ ; sđ$\overparen{BC}= 60^\circ $

Do đó $\widehat {ADC} = 30^\circ $.

Câu 15 :

Giải phương trình $\sqrt {2{x^2} - 4x + 5} = x - 2$ ta được nghiệm là

A.

$x = 1$
B.

$x = 3$
C.

$x = 2$
D.

Phương trình vô nghiệm

Đáp án : D

Phương pháp giải :

+ Tìm điều kiện

+ Giải phương trình dạng $\sqrt A = B\,\left( {B \ge 0} \right) \Leftrightarrow A = {B^2}$

Lời giải chi tiết :

Điều kiện:

$x - 2 \ge 0 \Leftrightarrow x \ge 2.$

Ta có: $\sqrt {2{x^2} - 4x + 5} = x - 2$$ \Leftrightarrow 2{x^2} - 4x + 5 = {\left( {x - 2} \right)^2}$

$ \Leftrightarrow 2{x^2} - 4x + 5 = {x^2} - 4x + 4 \Leftrightarrow {x^2} + 1 = 0$ $ \Leftrightarrow {x^2} = - 1\,$ (vô nghiệm vì ${x^2} \ge 0\,\,\forall x$ )

Vậy phương trình vô nghiệm.

Câu 16 :

Đường thẳng $y = a{\rm{x}} + b$ đi qua $2$ điểm $M\left( { - 3;2} \right)$ và $N\left( {1; - 1} \right)$ là:

A.

$y = - \dfrac{3}{4}x + \dfrac{1}{4}$
B.

$y = - \dfrac{3}{4}x - \dfrac{1}{4}$
C.

$y = - \dfrac{2}{3}x + \dfrac{1}{4}$
D.

$y = - \dfrac{3}{4}x + 1$

Đáp án : B

Phương pháp giải :

Sử dụng kiến thức:

+) Điểm $({x_0};{y_0})$ thuộc đồ thị hàm số $y = {\rm{ax}} + b$$ \Leftrightarrow {\rm{a}}{{\rm{x}}_0} + b = {y_0}$.

+) Từ đó tìm $a;b$.

Lời giải chi tiết :

Gọi $d:y = {\rm{ax}} + b$ đi qua $2$ điểm $M\left( { - 3;2} \right)$ và $N\left( {1; - 1} \right)$

$M$ thuộc $d \Leftrightarrow - 3a + b = 2 \Rightarrow b = 2 + 3a\,\,\,\,\,(1)$

$N$ thuộc $d \Leftrightarrow 1.a + b = - 1 \Rightarrow b = - 1 - a \,\,\,\,\,(2)$

Từ (1) và (2) suy ra $2 + 3a = - 1 - a \Leftrightarrow 4a = - 3 \Leftrightarrow a = - \dfrac{3}{4}$$ \Rightarrow b = 2 + 3a = - \dfrac{1}{4}$

Nên $a = \dfrac{{ - 3}}{4};b = - \dfrac{1}{4}$.

Vậy $d:y = - \dfrac{3}{4}x - \dfrac{1}{4}$.

Câu 17 :

Cho hai đường thẳng:

${d_1}:mx - 2\left( {3n + 2} \right)y = 6$ và ${d_2}:\left( {3m - 1} \right)x + 2ny = 56.$

Tìm tích $m. n$ để hai đường thẳng cắt nhau tại điểm $I\left( { - 2;3} \right)$.

A.

$0$
B.

$1$
C.

$2$
D.

$ - 2$

Đáp án : A

Phương pháp giải :

Bước 1: Sử dụng: đường thẳng $d:ax + by = c$ đi qua điểm $M\left( {{x_0};{y_0}} \right)$ để có được hai phương trình ẩn $m$ và $n$.

Bước 2: Giải hệ hai phương trình ẩn $m$ và $n$ bằng phương pháp thế để tìm $m$ và $n$. Từ đó suy ra tích $m.n$

Lời giải chi tiết :

+) Thay tọa độ điểm $I$ vào phương trình ${d_1}$ ta được $m.\left( { - 2} \right) - 2\left( {3n + 2} \right).3 = 6 \Leftrightarrow - 2m - 18n = 18 \Leftrightarrow m + 9n = - 9$

+) Thay tọa độ điểm $I$ vào phương trình ${d_2}$ ta được $\left( {3m - 1} \right).\left( { - 2} \right) + 2n.3 = 56 \Leftrightarrow - 6m + 2 + 6n = 56 \Leftrightarrow m - n = - 9$

Suy ra hệ phương trình $\left\{ \begin{array}{l}m + 9n = - 9\\m - n = - 9\end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l}m = - 9 + n\\ - 9 + n + 9n = - 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = - 9 + n\\10n = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}n = 0\\m = - 9\end{array} \right. \Rightarrow m.n = 0.$

Vậy $m.n = 0$.

Câu 18 :

Cho hệ phương trình $\left\{ \begin{array}{l}2x + by = - 1\\bx - 2ay = 1\end{array} \right.$. Biết rằng hệ phương trình có nghiệm là $\left( {1; - 2} \right)$, tính $a - b$.

A.

$\dfrac{{13}}{8}$
B.

$ - \dfrac{{13}}{8}$
C.

$\dfrac{5}{8}$
D.

$ - \dfrac{5}{8}$

Đáp án : B

Phương pháp giải :

Hệ phương trình bậc nhất hai ẩn có nghiệm $\left( {{x_0};{y_0}} \right) \Leftrightarrow \left\{ \begin{array}{l}a{x_0} + b{y_0} = c\\a'{x_0} + b'{y_0} = c'\end{array} \right..$

Lời giải chi tiết :

Thay $x = 1;y = - 2$ vào hệ ta được

$\left\{ \begin{array}{l}2.1 + b.\left( { - 2} \right) = - 1\\b.1 - 2a.\left( { - 2} \right) = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 2b = - 3\\b + 4a = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = \dfrac{3}{2}\\\dfrac{3}{2} + 4a = 1\end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l}b = \dfrac{3}{2}\\a = - \dfrac{1}{8}\end{array} \right. \Rightarrow a - b = - \dfrac{{13}}{8}$

Vậy $a - b = - \dfrac{{13}}{8}$.

Câu 19 :

A.

$2$
B.

$0$
C.

$-2$
D.

$1$

Đáp án : B

Lời giải chi tiết :

ĐK: $x \ge 0;y \ge 0$

Ta có $\left\{ \begin{array}{l}4\sqrt x - 3\sqrt y = 4\\2\sqrt x + \sqrt y = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4\sqrt x - 3\sqrt y = 4\\4\sqrt x + 2\sqrt y = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5\sqrt y = 0\\2\sqrt x + \sqrt y = 2\end{array} \right.$

$ \Leftrightarrow \left\{ \begin{array}{l}\sqrt y = 0\\2\sqrt x = 2\end{array} \right.$

$\Leftrightarrow \left\{ \begin{array}{l}y = 0\\x = 1\end{array} \right.$ (Thỏa mãn)

Vậy hệ phương trình có 1 nghiệm duy nhất $\left( {x;y} \right) = \left( {1;0} \right) \Rightarrow x.y = 0.$

Câu 20 :

Số nghiệm của hệ phương trình $\left\{ \begin{array}{l}5(x + 2y) - 3(x - y) = 99\\x - 3y = 7x - 4y - 17\end{array} \right.$là

A.

$2$
B.

Vô số
C.

$1$
D.

$0$

Đáp án : C

Phương pháp giải :

Giải hệ phương trình quy về hệ phương trình bậc nhất hai ẩn sau đó sử dụng phương pháp cộng đại số

Lời giải chi tiết :

Ta có $\left\{ \begin{array}{l}5(x + 2y) - 3(x - y) = 99\\x - 3y = 7x - 4y - 17\end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l}5x + 10y - 3x + 3y = 99\\x - 3y - 7x + 4y = - 17\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x + 13y = 99\\ - 6x + y = - 17\end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l}6x + 39y = 297\\ - 6x + y = - 17\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 6x + y = - 17\\40y = 280\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 7\\x = 4\end{array} \right.$

Vậy hệ phương trình có nghiệm duy nhất $\left( {x;y} \right) = \left( { 4;7} \right)$

Câu 21 :

A.

Hệ phương trình luôn có nghiệm duy nhất $\left( {x;y} \right)$ thỏa mãn $2x + y \le {\rm{3}}$
B.

Hệ phương trình luôn có nghiệm duy nhất $\left( {x;y} \right)$ thỏa mãn $2x + y > {\rm{3}}$
C.

Hệ phương trình luôn có nghiệm duy nhất $\left( {x;y} \right)$ thỏa mãn $2x + y \ge {\rm{3}}$
D.

Hệ phương trình luôn có nghiệm duy nhất $\left( {x;y} \right)$ thỏa mãn $2x + y = {\rm{3}}$

Đáp án : A

Phương pháp giải :

Bước 1: Giải hệ phương trình tìm được nghiệm $\left( {x,y} \right)$ theo tham số $m$

Bước 2: Thay $x,y$ vừa tìm được vào hệ thức yêu cầu để tìm $m$

Lời giải chi tiết :

Từ $\left( {m - 1} \right)x + y = 2$ thế vào phương trình còn lại ta được phương trình:

$mx + 2-\left( {m - 1} \right)x = m + 1 \Leftrightarrow x = m-1$ suy ra $y = 2-{\left( {m - 1} \right)^2}$ với mọi $m$

Vậy hệ phương trình luôn có nghiệm duy nhất $\left( {x;y} \right) = \left( {m - 1;2-{{\left( {m - 1} \right)}^2}} \right)$

$2x + {\rm{ }}y = 2\left( {m - 1} \right) + 2-{\left( {m - 1} \right)^2} = - {m^2} + 4m - 1$

$= 3-{\left( {m - 2} \right)^2} \le 3$ với mọi $m$.

Câu 22 :

A.

$6$ giờ
B.

$8$ giờ
C.

$10$ giờ
D.

$12$ giờ

Đáp án : B

Phương pháp giải :

Giải bài toán công việc (vòi nước) bằng cách lập hệ phương trình

Chúng ta vẫn sử dụng cách làm như bài toán làm chung công việc và coi bể nước là một công việc.

Lời giải chi tiết :

Gọi thời gian vòi I, vòi II chảy một mình đầy bể lần lượt là $x,y\,\,\left( {x,y > \dfrac{{24}}{5}} \right)$ (đơn vị: giờ)

Mỗi giờ vòi I chảy được $\dfrac{1}{x}$ (bể), vòi II chảy được $\dfrac{1}{y}$ bể nên cả hai vòi chảy được $\dfrac{1}{x} + \dfrac{1}{y}$ bể

Vì hai vòi nước cùng chảy vào một bể thì sau $4$ giờ $48$ phút $\left( { = \dfrac{{24}}{5}h} \right)$ bể đầy nên ta có phương trình

$\dfrac{1}{x} + \dfrac{1}{y} = \dfrac{5}{{24}}$

Nếu vòi I chảy riêng trong $4$ giờ, vòi II chảy riêng trong $3$ giờ thì cả hai vòi chảy được $\dfrac{3}{4}$ bể nên ta có phương trình $\dfrac{4}{x} + \dfrac{3}{y} = \dfrac{3}{4}$

Suy ra hệ phương trình $\left\{ \begin{array}{l}\dfrac{4}{x} + \dfrac{3}{y} = \dfrac{3}{4}\\\dfrac{1}{x} + \dfrac{1}{y} = \dfrac{5}{{24}}\end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l}\dfrac{4}{x} + \dfrac{3}{y} = \dfrac{3}{4}\\\dfrac{3}{x} + \dfrac{3}{y} = \dfrac{5}{8}\end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l}\dfrac{1}{x} = \dfrac{1}{8}\\\dfrac{1}{y} = \dfrac{1}{{12}}\end{array} \right.$

$\Leftrightarrow \left\{ \begin{array}{l}x = 8\\y = 12\end{array} \right.$ (Thỏa mãn)

Vậy thời gian vòi I một mình đầy bể là $8\,\,h$.

Câu 23 :

A.

$160$ dụng cụ
B.

$200$ dụng cụ.
C.

$120$ dụng cụ.
D.

$240$ dụng cụ.

Đáp án : A

Lời giải chi tiết :

Gọi số dụng cụ cần làm của xí nghiệp $1$ và xí nghiệp $2$ lần lượt là : $x,y$,

($x,y \in {N^*}$ $x,y < 360$, dụng cụ).

Số dụng cụ xí nghiệp $1$ và xí nghiệp $2$ làm được khi vượt mức lần lượt là $112\% x$ và $110\% y$ ( dụng cụ).

Ta có hệ phương trình : $\left\{ \begin{array}{l}x + y = 360\\112\% x + 110\% y = 400\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = 200\\y = 160\end{array} \right.$.

Vậy xí nghiệp $1$ phải làm $200$ dụng cụ, xí nghiệp $2$ phải làm $160$ dụng cụ.

Câu 24 :

Tìm các giá trị của $m$ để phương trình $m{x^2} - 2\left( {m - 2} \right)x + 3\left( {m - 2} \right) = 0$ có hai nghiệm phân biệt cùng dấu.

A.

$m < 0$
B.

$m > 1$
C.

$ - 1 < m < 0$
D.

$m > 0$

Đáp án : C

Phương pháp giải :

Xét phương trình $a{x^2} + bx + c = 0\left( {a \ne 0} \right)$. Khi đó phương trình có hai nghiệm cùng dấu $ \Leftrightarrow \left\{ \begin{array}{l}\Delta > 0\\P > 0\end{array} \right.$.

Lời giải chi tiết :

Phương trình $m{x^2} - 2\left( {m - 2} \right)x + 3\left( {m - 2} \right) = 0$$\left( {a = m;b = - 2\left( {m - 2} \right);c = 3\left( {m - 2} \right)} \right)$

Ta có $\Delta ' = {\left( {m - 2} \right)^2} - 3m\left( {m - 2} \right) = - 2{m^2} + 2m + 4 = \left( {4 - 2m} \right)\left( {m + 1} \right)$; $P = {x_1}.{x_2} = \dfrac{{3\left( {m - 2} \right)}}{m}$

Phương trình có hai nghiệm phân biệt cùng dấu khi $\left\{ \begin{array}{l}a \ne 0\\\Delta > 0\\P > 0\end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\\left( {4 - 2m} \right)\left( {m + 1} \right) > 0\\\dfrac{{3\left( {m - 2} \right)}}{m} > 0\end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\ - 1 < m < 2\\\left[ \begin{array}{l}m > 2\\m < 0\end{array} \right.\end{array} \right. \Rightarrow - 1 < m < 0$

Vậy $ - 1 < m < 0$ là giá trị cần tìm.

Câu 25 :

Tìm hai nghiệm của phương trình $18{x^2} + 23x + 5 = 0$ sau đó phân tích đa thức $A = 18{x^2} + 23x + 5$ sau thành nhân tử.

A.

${x_1} = - 1;{x_2} = - \dfrac{5}{{18}};$

$A = 18\left( {x + 1} \right)\left( {x + \dfrac{5}{{18}}} \right)$
B.

${x_1} = - 1;{x_2} = - \dfrac{5}{{18}};$

$A = \left( {x + 1} \right)\left( {x + \dfrac{5}{{18}}} \right)$
C.

${x_1} = - 1;{x_2} = \dfrac{5}{{18}};$

$A = 18\left( {x + 1} \right)\left( {x - \dfrac{5}{{18}}} \right)$
D.

${x_1} = 1;{x_2} = - \dfrac{5}{{18}};$

$A = 18\left( {x - 1} \right)\left( {x + \dfrac{5}{{18}}} \right)$

Đáp án : A

Phương pháp giải :

Bước 1 : Tìm hai nghiệm của phương trình đã cho

Bước 2 : Phân tích đa thức thành nhân tử bằng cách sử dụng

Nếu tam thức bậc hai $a{x^2} + bx + c{\rm{ }}\left( {a \ne 0} \right)$ có hai nghiệm ${x_1}$ và ${x_2}$ thì nó được phân tích thành nhân tử: $a{x^2} + bx + c = a\left( {x - {x_1}} \right)\left( {x - {x_2}} \right)$

Lời giải chi tiết :

Phương trình $18{x^2} + 23x + 5 = 0$ có $a - b + c = 18 - 23 + 5 = 0$ nê phương trình có hai nghiệm phân biệt là ${x_1} = - 1;{x_2} = - \dfrac{5}{{18}}$. Khi đó $A = 18.\left( {x + 1} \right)\left( {x + \dfrac{5}{{18}}} \right)$.

Câu 26 :

Phương trình $\left( {\dfrac{{1 + x}}{{1 - x}} - \dfrac{{1 - x}}{{1 + x}}} \right):\left( {\dfrac{{1 + x}}{{1 - x}} - 1} \right) = \dfrac{3}{{14 - x}}$ có nghiệm là:

A.

$x = \sqrt 2 $
B.

$x = 2$
C.

$x = 3$
D.

$x = 5$

Đáp án : D

Lời giải chi tiết :

Điều kiện: $x \ne 1;x \ne - 1;x \ne 14$

Ta có $\left( {\dfrac{{1 + x}}{{1 - x}} - \dfrac{{1 - x}}{{1 + x}}} \right):\left( {\dfrac{{1 + x}}{{1 - x}} - 1} \right) = \dfrac{3}{{14 - x}}$$ \Leftrightarrow \dfrac{{{{\left( {1 + x} \right)}^2} - {{\left( {1 - x} \right)}^2}}}{{\left( {1 - x} \right)\left( {1 + x} \right)}}:\dfrac{{1 + x - 1 + x}}{{1 - x}} = \dfrac{3}{{14 - x}}$

$ \Leftrightarrow \dfrac{{4x}}{{\left( {1 - x} \right)\left( {1 + x} \right)}}.\dfrac{{1 - x}}{{2x}} = \dfrac{3}{{14 - x}} \Leftrightarrow \dfrac{2}{{x + 1}} = \dfrac{3}{{14 - x}}$$ \Rightarrow 28 - 2x = 3x + 3 \Leftrightarrow 5x = 25 \Leftrightarrow x = 5\,\left( {TM} \right)$

Vậy phương trình có nghiệm $x = 5$

Câu 27 :

Phương trình $\dfrac{{2x}}{{x - 2}} - \dfrac{5}{{x - 3}} = \dfrac{{ - 9}}{{{x^2} - 5x + 6}}$có số nghiệm là

A.

$2$
B.

$1$
C.

$0$
D.

$3$

Đáp án : C

Lời giải chi tiết :

Điều kiện: $x \ne 2;x \ne 3$

$\dfrac{{2x}}{{x - 2}} - \dfrac{5}{{x - 3}} = \dfrac{-9}{{{x^2} - 5x + 6}}$$ \Leftrightarrow \dfrac{{2x\left( {x - 3} \right) - 5\left( {x - 2} \right)}}{{\left( {x - 2} \right)\left( {x - 3} \right)}} = \dfrac{{ - 9}}{{\left( {x - 2} \right)\left( {x - 3} \right)}}$$ \Rightarrow 2{x^2} - 11x + 19 = 0$

Nhận thấy $\Delta = {11^2} - 4.19.2 = - 31 < 0$ nên phương trình $2{x^2} - 11x + 19 = 0$ vô nghiệm. Suy ra phương trình đã cho vô nghiệm.

Câu 28 :

Tìm tham số $m$ để đường thẳng $d:y = mx + 2$ cắt parabol $\left( P \right):y = \dfrac{{{x^2}}}{2}$ tại hai điểm phân biệt

A.

$m = 2$
B.

$m = - 2$
C.

$m = 4$
D.

$m \in \mathbb{R}$

Đáp án : D

Phương pháp giải :

Bước 1: Xét phương trình hoành độ giao điểm của đường thẳng và parabol

Bước 2: Để đường thẳng cắt parabol tại hai điểm phân biệt thì phương trình hoành độ giao điểm có hai nghiệm phân biệt.

Lời giải chi tiết :

Xét phương trình hoành độ giao điểm $\dfrac{{{x^2}}}{2} = mx + 2 \Leftrightarrow {x^2} - 2mx - 4 = 0$ có $\Delta ' = {m^2} + 4$

Vì $\Delta ' = {m^2} + 4 > 0;\forall m$ nên đường thẳng $d:y = mx + 2$ cắt parabol $\left( P \right):y = \dfrac{{{x^2}}}{2}$ tại hai điểm phân biệt với mọi $m$.

Câu 29 :

Cho đường tròn $(O;R)$. Cát tuyến qua $A$ ở ngoài $(O)$ cắt $(O)$ tại $B$ và $C$. Cho biết $AB = BC$ và kẻ đường kính $COD$. Tính độ dài đoạn thẳng $AD.$

A.

$AD = R$
B.

$AD = 3R$
C.

$AD = \dfrac{R}{2}$
D.

$AD = 2R$

Đáp án : D

Phương pháp giải :

+) Nhắc lại : Cát tuyến là đường thẳng cắt đường tròn tại hai điểm.

+) Sử dụng Pytago để tính toán.

Lời giải chi tiết :

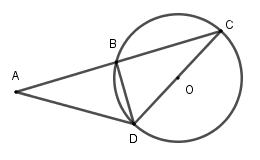
Xét $\left( O \right)$ có $OB = OC = OD$$ \Rightarrow BO = \dfrac{{DC}}{2}$$ \Rightarrow \Delta BDC$ vuông tại $B$ (tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh ấy thì tam giác đó là tam giác vuông)

Suy ra $BD \bot AC$.

Xét $\Delta ADC$ có $BD$ vừa là đường trung tuyến vừa là đường cao nên $\Delta ADC$ cân tại $D \Rightarrow DA = DC = 2R$

Vậy $AD = 2R.$

Câu 30 :

Hai tiếp tuyến tại $A$ và $B$ của đường tròn $(O)$ cắt nhau tại $I$ . Đường thẳng qua $I$ và vuông góc với $IA$ cắt $OB$ tại $K$. Chọn khẳng định đúng.

A.

$OI = OK = KI$
B.

$KI = KO$
C.

$OI = OK$
D.

$IO = IK$

Đáp án : B

Phương pháp giải :

Sử dụng tính chất hai tiếp tuyến cắt nhau và tính chất tam giác cân

Lời giải chi tiết :

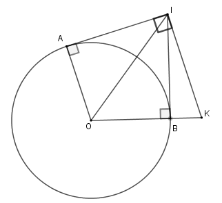
Xét $\left( O \right)$có $IA,IB$ là hai tiếp tuyến cắt nhau tại $I$ nên $\widehat {AOI} = \widehat {KOI}$

Mà $OA{\rm{//}}KI$ (vì cùng vuông góc với $AI$) nên $\widehat {KIO} = \widehat {IOA}$ (hai góc ở vị trí so le trong)

Từ đó $\widehat {KOI} = \widehat {KIO}$ suy ra $\Delta KOI$ cân tại $K \Rightarrow KI = KO$.

Câu 31 :

Hai tiếp tuyến tại $A$ và $B$ của đường tròn $\left( {O;R} \right)$ cắt nhau tại $M.$ Nếu $MA = \;R\sqrt 3 $ thì góc $\widehat {AOB}$ bằng:

A.

${120^0}\;$
B.

${90^0}$
C.

${60^0}$
D.

${45^0}$

Đáp án : A

Phương pháp giải :

Tính chất hai tiếp tuyến cắt nhau và tỉ số lượng giác của góc nhọn.

Lời giải chi tiết :

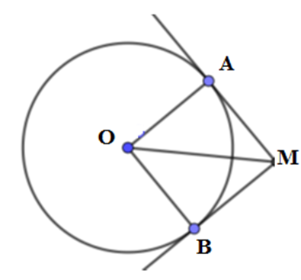
Có $AM$ là tiếp tuyến của đường tròn $\left( O \right)$ nên $AM$ vuông góc với $OA$

Xét tam giác $AOM$ vuông tại $A$ nên có $\tan \widehat {AOM} = \dfrac{{AM}}{{OA}} = \dfrac{{R\sqrt 3 }}{R} = \sqrt 3 $$ \Rightarrow \widehat {AOM} = {60^0}$

Mà hai tiếp tuyến $AM$ và $BM$ cắt nhau tại $M$ nên ta có $OM$ là phân giác của $\widehat {AOB}$

Vậy $\widehat {AOB}$$ = 2\widehat {AOM} = {2.60^0} = {120^0}$

Câu 32 :

Cho tam giác $ABC$ nội tiếp đường tròn $(O;R),$đường cao $AH,$ biết $AB = 9{\rm{ }}cm,$ $AC = 12{\rm{ }}cm,$ $AH = 4{\rm{ }}cm.$ Tính bán kính của đường tròn $(O)$.

A.

$13,5\,cm$
B.

$12\,cm$
C.

$18\,cm$
D.

$6\,cm$

Đáp án : A

Phương pháp giải :

Sử dụng kết quả câu trước.

Lời giải chi tiết :

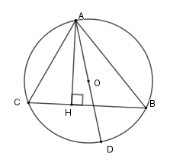
Kẻ đường kính $AD$, theo kết quả câu trước, ta có $AH.AD = AB.AC$ $ \Rightarrow AD = \dfrac{{AB.AC}}{{AH}} = \dfrac{{9.12}}{4} = 27 \Rightarrow R = 13,5cm$ .

Câu 33 :

Cho đường tròn $(O)$ và hai dây cung $AB,AC$ bằng nhau. Qua $A$ vẽ một cát tuyến cắt dây $BC$ ở $D$ và cắt $(O)$ ở $E$. Khi đó $A{B^2}$ bằng

A.

$AD.AE$
B.

$AD.AC$
C.

$AE.BE$
D.

$AD.BD$

Đáp án : A

Phương pháp giải :

Sử dụng hệ quả của góc nội tiếp để chứng minh các góc bằng nhau và suy ra tam giác đồng dạng

Từ đó có hệ thức cần chứng minh.

Lời giải chi tiết :

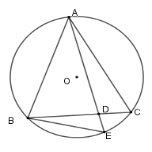
Xét $\left( O \right)$ có $\widehat {AEB} = \widehat {ABC}$ (hai góc nội tiếp chắn hai cung bằng nhau $AB = AC$ )

Xét $\Delta ABD$ và $\Delta AEB$ có $\widehat A$ chung và $\widehat {AEB} = \widehat {ABC}$ (cmt) nên $\Delta ABD\backsim\Delta AEB\left( {g - g} \right) \Rightarrow \dfrac{{AB}}{{AE}} = \dfrac{{AD}}{{AB}} \Rightarrow A{B^2} = AE.AD$

Câu 34 :

A.

$IE = IF$
B.

$IE = 2IF$
C.

$EF = 3IE$
D.

$EF = 3IF$

Đáp án : A

Phương pháp giải :

Sử dụng hệ quả góc tạo bởi tia tiếp tuyến và dây cung để chứng minh hai góc bằng nhau.

Lời giải chi tiết :

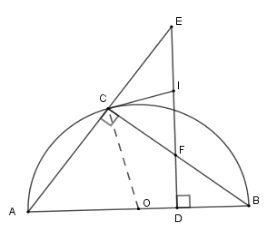
Xét $\left( O \right)$ có $\widehat {ICB} = \widehat {CAB}$ (hệ quả) mà $\widehat {BFD} = \widehat {BAC}$ (cùng phụ với $\widehat {ABC}$ )

Nên $\widehat {ICF} = \widehat {BFD} \Rightarrow \widehat {ICF} = \widehat {CFI}$ suy ra $\Delta ICF$ cân tại $I \Rightarrow IF = IC$ (*)

Lại có $\widehat {ICE} + \widehat {ICF} = 90^\circ \Rightarrow \widehat {ICE} + \widehat {CAB} = 90^\circ $ mà $\widehat {CAB} + \widehat {AED} = 90^\circ \Rightarrow \widehat {CEI} = \widehat {ECI} \Rightarrow \Delta ICE$ cân tại $I$

Nên $IE = IC$ (**)

Từ (*) và (**) suy ra $IE = IF = \dfrac{{EF}}{2}$ .

Câu 35 :

A.

$A{B^2}$
B.

$B{C^2}$
C.

$A{C^2}$
D.

$A{M^2}$

Đáp án : A

Phương pháp giải :

Sử dụng hệ quả về góc tạo bởi tiếp tuyến và dây cung để chứng minh các góc bằng nhau

Lời giải chi tiết :

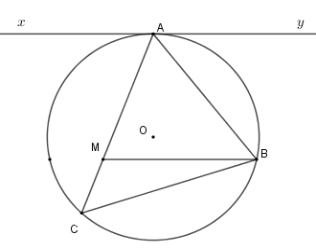
Ta có $\widehat {yAB} = \widehat {ACB}$ (hệ quả) mà $\widehat {yAB} = \widehat {ABM}$ (so le trong) nên $\widehat {ACB} = \widehat {ABM} \Rightarrow \Delta AMB\backsim\Delta ABC\left( {g - g} \right)$

$\dfrac{{AM}}{{AB}} = \dfrac{{AB}}{{AC}} \Rightarrow AM.AC = A{B^2}$ .

Câu 36 :

A.

Tứ giác $ABCD$ nội tiếp.
B.

$\widehat {ABD} = \widehat {ACD}$
C.

$CA$ là phân giác của $\widehat {SCB}.$
D.

Tứ giác $ABCS$ nội tiếp.

Đáp án : D

Phương pháp giải :

Góc nội tiếp chắn nửa đường tròn là góc vuông.

Dấu hiệu nhận biết tứ giác nội tiếp:

+) Tứ giác có tổng hai góc đối diện bằng ${180^0}.$

+) Tứ giác có hai đỉnh kề một cạnh cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc $\alpha .$

+) Tứ giác có bốn đỉnh cách đều một điểm, điểm đó là tâm của đường tròn ngoại tiếp tứ giác.

+) Tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối của đỉnh đó.

Lời giải chi tiết :

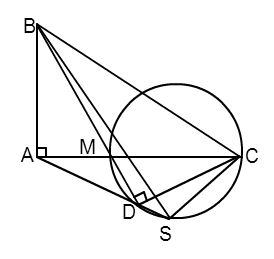
+) Ta có: $\widehat {MDC}$ là góc nội tiếp chắn nửa đường tròn đường kính $MC$ $ \Rightarrow \widehat {MDC} = {90^0}$ (tính chất góc nội tiếp).

Xét tứ giác $ABCD$ ta có:

Góc $BAC$ và góc $BDC$ cùng nhìn đoạn $BC$ dưới góc ${90^0}.$

$ \Rightarrow $ $ABCD$ là tứ giác nội tiếp (dhnb) $ \Rightarrow $ phương án A đúng.

+) Xét tứ giác $ABCD$ nội tiếp ta có$\widehat {ABD} = \widehat {ACD}$ (cùng nhìn đoạn $AD$ )$ \Rightarrow $ phương án B đúng.

+) Xét đường tròn đường kính $MC$ ta có $4$ điểm $M,C,D,S$ cùng thuộc đường tròn.

$ \Rightarrow $ Tứ giác $MCSD$ là tứ giác nội tiếp.

$ \Rightarrow \widehat {ADM} = \widehat {SCM}$ (góc ngoài tại $1$ đỉnh bằng góc trong tại đỉnh đối diện). $\left( 1 \right)$

Vì tứ giác $ABCD$ nội tiếp (cmt) $ \Rightarrow \widehat {ACB} = \widehat {ADB}$ (cùng nhìn đoạn$AB$ ) $\left( 2 \right)$

Từ $\left( 1 \right)$ và $\left( 2 \right)$ $ \Rightarrow \widehat {BCA} = \widehat {ACS}\;\;\;\left( { = \widehat {ADB}} \right).$

Hay $CA$ là phân giác của $\widehat {SCB} \Rightarrow $ phương án C đúng.

+) Giả sử tứ giác $ABCS$ là tứ giác nội tiếp $ \Rightarrow \widehat {ASB} = \widehat {BCA}$ (hai góc cùng nhìn đoạn $AB$ ).

Mà $\widehat {ACB} = \widehat {BDA};\;\;\;\widehat {BAD} \ne \widehat {BSA}$ (xét trong đường tròn đường kính $CM$ )

$ \Rightarrow \widehat {ASB} \ne \widehat {BCA} \Rightarrow $ tứ giác $ABCS$ không là tứ giác nội tiếp $ \Rightarrow $phương án D sai.

Câu 37 :

A.

Bốn điểm $O,E,M,N$ cùng thuộc một đường tròn
B.

$N{E^2} = NC.NB$
C.

$\widehat {NEH} = \widehat {NME}$
D.

$\widehat {NFO} < 90^\circ $

Đáp án : D

Phương pháp giải :

* Sử dụng dấu hiệu nhận biết tứ giác nội tiếp:

+) Tứ giác có tổng hai góc đối diện bằng ${180^0}.$

+) Tứ giác có hai đỉnh kề một cạnh cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc $\alpha .$

+) Tứ giác có bốn đỉnh cách đều một điểm, điểm đó là tâm của đường tròn ngoại tiếp tứ giác.

+) Tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối của đỉnh đó.

* Sử dụng tam giác đồng dạng.

Lời giải chi tiết :

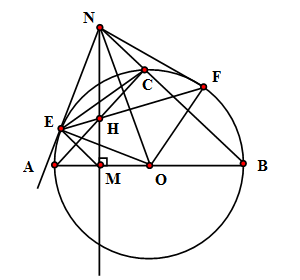
+) Vì $\widehat {NEO} = \widehat {NMO} = 90^\circ \Rightarrow NEMO$ là tứ giác nội tiếp nên bốn điểm $O,E,M,N$ cùng thuộc một đường tròn

$ \Rightarrow $ Phương án A đúng.

+) $\widehat {NEC} = \widehat {CBE} = \dfrac{1}{2}$ số đo cung $CE \Rightarrow \Delta NEC\backsim\Delta NBE\left( {g - g} \right) \Rightarrow \dfrac{{NE}}{{NB}} = \dfrac{{NC}}{{NE}}$ $ \Rightarrow NB.NC = N{E^2}$

$ \Rightarrow $ Phương án B đúng.

+) Hai tam giác vuông $\Delta NCH\backsim\Delta NMB\left( {g - g} \right) $

$\Rightarrow \dfrac{{NC}}{{NM}} = \dfrac{{NH}}{{NB}} $

$\Rightarrow NC.NB=NH.NM$

Từ đó $\Delta NEH\backsim\Delta NME\left( {c-g -c} \right) \Rightarrow \widehat {NEH} = \widehat {EMN}$ $ \Rightarrow $ Phương án C đúng.

+) $\widehat {EMN} = \widehat {EON}$ (tứ giác $NEMO$ nội tiếp) $ \Rightarrow \widehat {NEH} = \widehat {NOE}$

Mà góc $ENO$ phụ với góc $EON$ nên góc $ENO$ cũng phụ với góc $NEH$

$\Rightarrow EH \bot NO$

$ \Rightarrow \Delta OEF$ cân có $ON$ là phân giác

$ \Rightarrow \widehat {EON} = \widehat {NOF} \Rightarrow \widehat {NEF} = \widehat {NOF}$ nên tứ giác $NEOF$ nội tiếp $ \Rightarrow \widehat {NFO} = 180^\circ - \widehat {NEO} = 90^\circ $ .

$ \Rightarrow $ Phương án D sai.

Câu 38 :

Cho $A = \dfrac{{2x}}{{x + 3\sqrt x + 2}} + \dfrac{{5\sqrt x + 1}}{{x + 4\sqrt x + 3}} + \dfrac{{\sqrt x + 10}}{{x + 5\sqrt x + 6}}$ với $x \ge 0$. Chọn đáp án đúng.

A.

$A = 2\sqrt x $
B.

Giá trị của $A$ không phụ thuộc vào biến $x.$
C.

$A = 3\left( {\sqrt x + 2} \right)$
D.

$A = \dfrac{2}{{\sqrt x + 1}}$

Đáp án : B

Phương pháp giải :

+ Phân tích mẫu thức thành nhân tử rồi qui đồng mẫu các phân thức

+ Từ đó rút gọn phân thức

Lời giải chi tiết :

$A = \dfrac{{2x}}{{x + 3\sqrt x + 2}} + \dfrac{{5\sqrt x + 1}}{{x + 4\sqrt x + 3}} + \dfrac{{\sqrt x + 10}}{{x + 5\sqrt x + 6}}$$= \dfrac{{2x}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x + 2} \right)}} + \dfrac{{5\sqrt x + 1}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x + 3} \right)}} + \dfrac{{\sqrt x + 10}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x + 3} \right)}}$

$ = \dfrac{{2x\left( {\sqrt x + 3} \right) + \left( {5\sqrt x + 1} \right)\left( {\sqrt x + 2} \right) + \left( {\sqrt x + 10} \right)\left( {\sqrt x + 1} \right)}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x + 2} \right)\left( {\sqrt x + 3} \right)}}$

$ = \dfrac{{2x\sqrt x + 6x + 5x + 11\sqrt x + 2 + x + 11\sqrt x + 10}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x + 2} \right)\left( {\sqrt x + 3} \right)}}$

$ = \dfrac{{2x\sqrt x + 12x + 22\sqrt x + 12}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x + 2} \right)\left( {\sqrt x + 3} \right)}}$

$ = \dfrac{{2x\sqrt x + 2x + 10x + 10\sqrt x + 12\sqrt x + 12}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x + 2} \right)\left( {\sqrt x + 3} \right)}}$

$\begin{array}{l} = \dfrac{{2x\left( {\sqrt x + 1} \right) + 10\sqrt x \left( {\sqrt x + 1} \right) + 12\left( {\sqrt x + 1} \right)}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x + 2} \right)\left( {\sqrt x + 3} \right)}}\\ = \dfrac{{\left( {\sqrt x + 1} \right)\left( {2x + 10\sqrt x + 12} \right)}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x + 2} \right)\left( {\sqrt x + 3} \right)}}\\
= \dfrac{{2\left( {x + 5\sqrt x + 6} \right)}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x + 3} \right)}}\\
= \dfrac{{2\left( {x + 2\sqrt x + 3\sqrt x + 6} \right)}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x + 3} \right)}}\\
= \dfrac{{2\left[ {\sqrt x \left( {\sqrt x + 2} \right) + 3\left( {\sqrt x + 2} \right)} \right]}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x + 3} \right)}}\\= \dfrac{{2\left( {\sqrt x + 1} \right)\left( {\sqrt x + 2} \right)\left( {\sqrt x + 3} \right)}}{{\left( {\sqrt x + 1} \right)\left( {\sqrt x + 2} \right)\left( {\sqrt x + 3} \right)}}\\ = 2\end{array}$

Vậy giá trị của $A$ không phụ thuộc vào biến $x.$

Câu 39 :

A.

$\dfrac{{27}}{6}$ ( đvdt)
B.

$27$( đvdt)
C.

$\dfrac{{27}}{2}$ (đvdt)
D.

$\dfrac{{27}}{4}$(đvdt)

Đáp án : D

Phương pháp giải :

- Xác định giao điểm 2 đường thẳng đã cho

- Dựng đường cao của tam giác được tạo thành

- Tính độ dài các đoạn thẳng

- Tính diện tích tam giác.

Lời giải chi tiết :

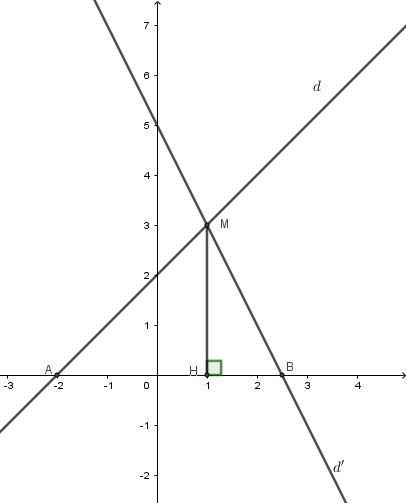
Xét phương trình hoành độ giao điểm của ${d_1};{d_2}$

$x + 2 = - 2x + 5 \Leftrightarrow x = 1 \Rightarrow y = 3 \Rightarrow {d_1} \cap {d_2}$ tại $ M(1;3)$

Gọi $H$ là chân đường vuông góc kẻ từ $M$ tới $Ox$. Suy ra $MH = 3$

$d \cap Ox$ tại $ A( - 2;0) \Rightarrow OA = 2$

$d' \cap Ox$ tại $ B\left( {\dfrac{5}{2};0} \right) \Rightarrow OB = \dfrac{5}{2}$

$\Rightarrow AB = OA+OB=2 + \dfrac{5}{2} = \dfrac{9}{2}$

${S_{MAB}} = \dfrac{1}{2}AB.MH = \dfrac{1}{2}.\dfrac{9}{2}.3 = \dfrac{{27}}{4}\,(dvdt)$

Câu 40 :

A.

$\Delta ABC$ cân
B.

$\Delta ABC$ đều.
C.

$\Delta ABC$ vuông cân
D.

$\Delta ABC$ vuông

Đáp án : B

Phương pháp giải :

Kẻ $AH \bot BC,\,OI \bot BC$, đường kính $AD.$

Sử dụng tính chất góc nội tiếp chắn nửa đường tròn để chứng minh $\widehat {ABD} = {90^0} \Rightarrow \Delta ABD \backsim \Delta AHC$.

Tính độ dài $AH$ từ tính chất hai tam giác đồng dạng, từ đó suy ra điều kiện để diện tích tam giác $ABC$ lớn nhất.

Lời giải chi tiết :

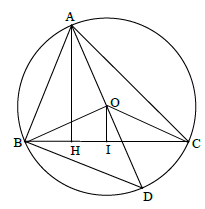
Kẻ $AH \bot BC,\,OI \bot BC$, đường kính $AD.$

Ta chứng minh được $\Delta AHC \backsim \Delta ABD\,\left( {g - g} \right).$

Do đó $\dfrac{{AH}}{{AB}} = \dfrac{{AC}}{{AD}} \Rightarrow AH.AD = AB.AC $$\Rightarrow AB.AC = 2R.AH\,\,\left( 1 \right).$

Theo giả thiết $\sqrt {AB.AC} = R\sqrt 3 ,$ nên $AB.AC = 3{R^2}\,\,\left( 2 \right).$

Thay $\left( 2 \right)$ và $\left( 1 \right)$ ta có $AH = \dfrac{{3R}}{2}.$

Lại có $OI + OA \ge AI \ge AH$ nên $OI \ge AH - OA = \dfrac{{3R}}{2} - R = \dfrac{R}{2}.$

Do $AH = \dfrac{{3R}}{2}$ là giá trị không đổi nên ${S_{ABC}}$ lớn nhất khi $BC$ lớn nhất $ \Leftrightarrow OI$ nhỏ nhất

$ \Leftrightarrow OI = \dfrac{R}{2} \Leftrightarrow BC \bot OA \Rightarrow \Delta ABC$ cân tại $A$.

Mà $OI = \dfrac{R}{2} \Rightarrow \sin \widehat {OBI} $$= \dfrac{{OI}}{{OB}} = \dfrac{1}{2}$$ \Rightarrow \widehat {OBI} = \widehat {OCI} = {30^0} $$\Rightarrow \widehat {BOC} $$= {120^0}$$ \Rightarrow \widehat {BAC} = {60^0}$

Vậy $\Delta ABC$ đều.