Đề kiểm tra học kì 2 Toán 8 - Đề số 5
Đề bài
Tổng các nghiệm của phương trình \(\left( {{x^2} - 4} \right)\left( {x + 6} \right)\left( {x - 8} \right) = 0\) là:
-
A.
\(1\)
-
B.
\(2\)
-
C.
\(3\)
-
D.
\(4\)
Chọn khẳng định đúng.
-
A.
Phương trình \(8x\left( {3x - 5} \right) = 6\left( {3x - 5} \right)\)có hai nghiệm trái dấu
-
B.
Phương trình \(8x\left( {3x - 5} \right) = 6\left( {3x - 5} \right)\)có hai nghiệm cùng dương
-
C.
Phương trình \(8x\left( {3x - 5} \right) = 6\left( {3x - 5} \right)\)có hai nghiệm cùng âm
-
D.
Phương trình \(8x\left( {3x - 5} \right) = 6\left( {3x - 5} \right)\)có một nghiệm duy nhất
Cho phương trình \(\left( 1 \right)\): \(\dfrac{1}{x} + \dfrac{2}{{x - 2}} = 0\) và phương trình \(\left( 2 \right)\): \(\dfrac{{x - 1}}{{x + 2}} - \dfrac{x}{{x - 2}} = \dfrac{{5x - 2}}{{4 - {x^2}}}\). Khẳng định nào sau đây là đúng.
-
A.
Hai phương trình có cùng điều kiện xác định.
-
B.
Hai phương trình có cùng số nghiệm
-
C.
Phương trình \(\left( 2 \right)\) có nhiều nghiệm hơn phương trình \(\left( 1 \right)\)
-
D.
Hai phương trình tương đương
Biết \({x_0}\) là nghiệm nhỏ nhất của phương trình
\(\dfrac{1}{{{x^2} + 4x + 3}} + \dfrac{1}{{{x^2} + 8x + 15}} + \dfrac{1}{{{x^2} + 12x + 35}} + \dfrac{1}{{{x^2} + 16x + 63}} = \dfrac{1}{5}.\) Chọn khẳng định đúng.
-
A.
\({x_0} > 0\)
-
B.
\({x_0} < - 5\)
-
C.
\({x_0} = - 10\)
-
D.
\({x_0} > 5\)
Hai xe khởi hành cùng một lúc, xe thứ nhất đến sớm hơn xe thứ hai $3$ giờ. Nếu gọi thời gian đi của xe thứ nhất là $x$ giờ thì thời gian đi của xe thứ hai là:
-
A.
\((x - 3)\) giờ
-
B.
\(3x\) giờ
-
C.
\((3 - x)\) giờ
-
D.
\((x + 3)\) giờ
Một tổ sản xuất theo kế hoạch mỗi ngày phải sản xuất $50$ sản phầm. Khi thực hiện tổ đã sản xuất được $57$ sản phẩm một ngày. Do đó hoàn thành trước kế hoạch $1$ ngày và còn vượt mức $13$ sản phẩm. Hỏi theo kế hoạch tổ phải sản xuất bao nhiêu sản phẩm?
-
A.
\(550\)
-
B.
\(400\)
-
C.
\(600\)
-
D.
\(500\)
Tìm số tự nhiên có bốn chữ số, biết rằng nếu viết thêm chữ số $1$ vào đằng trước ta được số $A$ có năm chữ số, nếu viết them chữ số $4$ vào đằng sau ta được số $B$ có năm chữ số, trong đó $B$ gấp bốn lần $A$ .
-
A.
$6789$
-
B.
$6666$
-
C.
$6699$
-
D.
$9999$
Cho \(a > b\) khi đó
-
A.
\(a - b > 0\)
-
B.
\(a - b < 0\)
-
C.
\(a - b = 0\)
-
D.
\(a - b \le 0\)
Cho \(a + 8 < b\). So sánh \(a - 7\) và \(b - 15\)
-
A.
\(a - 7 < b - 15\)
-
B.
\(a - 7 > b - 15\)
-
C.
\(a - 7 \ge b - 15\)
-
D.
\(a - 7 \le b - 15\)
Với \(a,b\) bất kỳ. Chọn khẳng định sai.
-
A.
\({a^2} + 5 > 4a\)
-
B.
\({a^2} + 10 < 6a - 1\)
-
C.
\({a^2} + 1 > a\)
-
D.
\(ab - {b^2} \le {a^2}\)
Cho $a,b$ bất kì. Chọn câu đúng.
-
A.
\(\dfrac{{{a^2} + {b^2}}}{2} < ab\)
-
B.
\(\dfrac{{{a^2} + {b^2}}}{2} \le ab\)
-
C.
\(\dfrac{{{a^2} + {b^2}}}{2} \ge ab\)
-
D.
\(\dfrac{{{a^2} + {b^2}}}{2} > ab\)
Bất đẳng thức nào sau đây đúng với mọi \(a > 0,b > 0:\)
-
A.
\({a^3} + {b^3} - a{b^2} - {a^2}b < 0\)
-
B.
\({a^3} + {b^3} - a{b^2} - {a^2}b \ge 0\)
-
C.
\({a^3} + {b^3} - a{b^2} - {a^2}b \le 0\)
-
D.
\({a^3} + {b^3} - a{b^2} - {a^2}b > 0\)
Hãy chọn câu sai. Cho hình vẽ với $AB<AC$:
-
A.
\(\dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}} \Rightarrow DE//BC\).
-
B.
\(\dfrac{{AD}}{{DB}} = \dfrac{{AE}}{{EC}} \Rightarrow DE//BC\).
-
C.
\(\dfrac{{AB}}{{DB}} = \dfrac{{AC}}{{EC}} \Rightarrow DE//BC\).
-
D.
\(\dfrac{{AD}}{{DE}} = \dfrac{{AE}}{{ED}} \Rightarrow DE//BC\).
Cho hình vẽ, trong đó $DE{\rm{//}}BC$, $AD = 12,\,\,DB = 18,\,\,CE = 30$. Độ dài $AC$ bằng:
-
A.
\(20\)
-
B.
\(\dfrac{{18}}{{25}}\)
-
C.
\(50\)
-
D.
\(45\)
Chọn câu trả lời đúng: Cho hình bên, biết \(DE{\rm{//}}AC\), tìm \(x\) :
-
A.
\(x = 6,5\)
-
B.
\(x = 6,25\)
-
C.
\(x = 5\)
-
D.
\(x = 8\)\(\)
Cho tứ giác \(ABCD\), lấy bất kỳ \(E \in BD\) . Qua \(E\) vẽ \(EF\) song song với \(AD\)( \(F\) thuộc \(AB\)), vẽ \(EG\) song song với \(DC\)(\(G\) thuộc\(BC\)). Chọn khẳng định sai.
-
A.
\(\dfrac{{BE}}{{ED}} = \dfrac{{BG}}{{GC}}\)
-
B.
\(\dfrac{{BF}}{{FA}} = \dfrac{{BG}}{{GC}}\)
-
C.
\(FG{\rm{//}}AC\)
-
D.
\(FG{\rm{//}}AD\)\(\)
Cho tam giác ABC có AM là đường trung tuyến, N là điểm trên đoạn thẳng AM. Gọi D là giao điểm của CN và AB, E là giao điểm của BN và AC. Chọn khẳng định đúng nhất.
-
A.
\(DE{\rm{//}}BC\)
-
B.
\(\dfrac{{AD}}{{BD}} = \dfrac{{AE}}{{CE}}\)
-
C.
Cả A, B đều đúng
-
D.
Cả A, B đều sai\(\)
Hãy chọn câu đúng. Nếu $\Delta ABC$ và $\Delta DEF$ có $\widehat B = \widehat {D;}\,\dfrac{{BA}}{{BC}} = \dfrac{{DE}}{{DF}}$ thì:
-
A.
$\Delta ABC$ đồng dạng với $\Delta DEF$
-
B.
$\Delta ABC$ đồng dạng với $\Delta EDF$
-
C.
$\Delta BCA$ đồng dạng với $\Delta DEF$
-
D.
$\Delta ABC$ đồng dạng với $\Delta FDE$
Cho $\Delta DHE \backsim\Delta ABC$ với tỉ số đồng dạng $\dfrac{2}{3}$. Có bao nhiêu khẳng định đúng trong các khẳng định sau:
(I) Tỉ số hai đường cao tương ứng của $\Delta DHE$ và $\Delta ABC$ là $\dfrac{2}{3}$.
(II) Tỉ số hai đường cao tương ứng của $\Delta ABC$ và $\Delta DHE$ là $\dfrac{2}{3}$.
(III) Tỉ số diện tích của $\Delta ABC$ và $\Delta DHE$ là $\dfrac{2}{3}$.
(IV) Tỉ số diện tích của $\Delta DHE$ và $\Delta ABC$ là $\dfrac{4}{9}$.
-
A.
\(2\)
-
B.
\(1\)
-
C.
\(3\)
-
D.
\(4\)
Hãy chọn câu đúng. Hình hộp chữ nhật có ba kích thước lần lượt là: $a$, $2a$, $\dfrac{a}{2}$ thể tích của hình hộp chữ nhật đó là:
-
A.
${a^2}$
-
B.
$4{a^2}$
-
C.
$2{a^4}$
-
D.
${a^3}$
Các kích thước của hình hộp chữ nhật \(ABC{\rm{D}}.A'B'C'D'\) là $DC = 6cm$ , $CB = 3cm$ . Hỏi độ dài của \(A'B'\) và $AD$ là bao nhiêu $cm$ ?
-
A.
$3\,cm$ và $6\,cm$
-
B.
$6\,cm$ và $9\,cm$
-
C.
$6\,cm$ và $3\,cm$
-
D.
$9\,cm$ và $6\,cm$
Thể tích của hình chóp tứ giác đều có chiều cao $6$ cm, cạnh đáy $4$ cm là
-
A.
$32\,c{m^3}$
-
B.
$24\,c{m^3}$
-
C.
$144\,c{m^3}$
-
D.
$96\,c{m^3}$
Phương trình \({x^2} + x = 0\) có số nghiệm là
-
A.
1 nghiệm
-
B.
2 nghiệm
-
C.
vô nghiệm
-
D.
vô số nghiệm
Phương trình \(\dfrac{x}{{x - 5}} - \dfrac{3}{{x - 2}} = 1\) có nghiệm là
-
A.
\(x = - \dfrac{1}{2}\)
-
B.
\(x = \dfrac{5}{2}\)
-
C.
\(x = \dfrac{1}{2}\)
-
D.
\(x = - \dfrac{5}{2}\)
Phương trình \(\dfrac{{x - 1}}{2} + \dfrac{{x - 1}}{3} - \dfrac{{x - 1}}{6} = 2\) có tập nghiệm là
-
A.
\(S = \left\{ {0;1} \right\}\)
-
B.
\(S = \left\{ 4 \right\}\)
-
C.
\(S = \emptyset \)
-
D.
\(S = \mathbb{R}\)
Tích các nghiệm của phương trình: \(\left( {{x^2} - 3x + 3} \right)\left( {{x^2} - 2x + 3} \right) = 2{x^2}\) là
-
A.
\( - 2\)
-
B.
\(2\)
-
C.
\(4\)
-
D.
\(3\)
Nghiệm của bất phương trình $7(3x + 5) > 0$ là:
-
A.
$x > \dfrac{3}{5}$
-
B.
$x \le - \dfrac{5}{3}$
-
C.
$x \ge - \dfrac{5}{3}$
-
D.
$x > - \dfrac{5}{3}$.
Với giá trị nào của $m$ thì bất phương trình $m(2x + 1) < 8$ là bất phương trình bậc nhất một ẩn?
-
A.
$m \ne 1$
-
B.
$m \ne - \dfrac{1}{3}$
-
C.
$m \ne 0$
-
D.
$m \ne 8$.
Số nguyên nhỏ nhất thỏa mãn bất phương trình $x(5x + 1) + 4(x + 3) > 5{x^2}$ là
-
A.
$x = - 3$
-
B.
$x = 0$
-
C.
\(x = - 1\)
-
D.
\(x = - 2\).
Tích các nghiệm của phương trình $|{x^2} + 2x - 1| = 2$ là
-
A.
\(3\)
-
B.
\( - 3\)
-
C.
\(1\)
-
D.
\( - 1\).
Giải phương trình \({\left| {x - 3y} \right|^{2017}} + {\left| {y + 4} \right|^{2018}} = 0\) ta được nghiệm \(\left( {x;y} \right)\). Khi đó \(y - x\) bằng
-
A.
\( - 16\)
-
B.
\( - 8\)
-
C.
\(16\)
-
D.
\(8\).
Tính diện tích toàn phần hình chóp tứ giác đều dưới đây:
-
A.
\(600\;c{m^2}\)
-
B.
\(700\;c{m^2}\)
-
C.
\(800\;c{m^2}\)
-
D.
\(900\;c{m^2}\)
Lời giải và đáp án
Tổng các nghiệm của phương trình \(\left( {{x^2} - 4} \right)\left( {x + 6} \right)\left( {x - 8} \right) = 0\) là:
-
A.
\(1\)
-
B.
\(2\)
-
C.
\(3\)
-
D.
\(4\)
Đáp án : B
Ta sử dụng \(A\left( x \right).B\left( x \right).C\left( x \right) = 0\) thì \( A\left( x \right) = 0\) hoặc \(B\left( x \right) = 0\) hoặc \(C\left( x \right) = 0\).
Ta có \(\left( {{x^2} - 4} \right)\left( {x + 6} \right)\left( {x - 8} \right) = 0\)
\(+)\,{x^2} - 4 = 0\\{x^2} = 4\)
Suy ra \(x = 2\) hoặc \(x = - 2\)
\(+)\,x + 6 = 0\\x = - 6\)
\(+)\,x - 8 = 0\\x = 8\)
Tổng các nghiệm của phương trình là: \(2 + \left( { - 2} \right) + \left( { - 6} \right) + 8 = 2\) .
Chọn khẳng định đúng.
-
A.
Phương trình \(8x\left( {3x - 5} \right) = 6\left( {3x - 5} \right)\)có hai nghiệm trái dấu
-
B.
Phương trình \(8x\left( {3x - 5} \right) = 6\left( {3x - 5} \right)\)có hai nghiệm cùng dương
-
C.
Phương trình \(8x\left( {3x - 5} \right) = 6\left( {3x - 5} \right)\)có hai nghiệm cùng âm
-
D.
Phương trình \(8x\left( {3x - 5} \right) = 6\left( {3x - 5} \right)\)có một nghiệm duy nhất
Đáp án : B
Ta biến đổi phương trình đã cho về dạng \(A\left( x \right).B\left( x \right) = 0 \Leftrightarrow A\left( x \right) = 0\) hoặc \(B\left( x \right) = 0\)
Ta có \(8x\left( {3x - 5} \right) = 6\left( {3x - 5} \right)\)
\(8x\left( {3x - 5} \right) - 6\left( {3x - 5} \right) = 0\\ \left( {8x - 6} \right)\left( {3x - 5} \right) = 0\)
\(+)\,8x - 6 = 0\\8x = 6\\x = \dfrac{3}{4}\)
\(+)\,3x - 5 = 0\\3x = 5\\x = \dfrac{5}{3}\)
Vậy phương trình đã cho có hai nghiệm cùng dương \(x = \dfrac{3}{4};\,x = \dfrac{5}{3}\) .
Một số em thấy nhân tử \(\left( {3x - 5} \right)\) xuất hiện ở cả hai vế nên đã rút gọn, dẫn đến còn lại \(8x = 6\) . Do đó bị thiếu nghiệm \(x = \dfrac{5}{3}\) .
Cho phương trình \(\left( 1 \right)\): \(\dfrac{1}{x} + \dfrac{2}{{x - 2}} = 0\) và phương trình \(\left( 2 \right)\): \(\dfrac{{x - 1}}{{x + 2}} - \dfrac{x}{{x - 2}} = \dfrac{{5x - 2}}{{4 - {x^2}}}\). Khẳng định nào sau đây là đúng.
-
A.
Hai phương trình có cùng điều kiện xác định.
-
B.
Hai phương trình có cùng số nghiệm
-
C.
Phương trình \(\left( 2 \right)\) có nhiều nghiệm hơn phương trình \(\left( 1 \right)\)
-
D.
Hai phương trình tương đương
Đáp án : C
Giải từng phương trình theo các bước sau và kết luận.
+ Tìm ĐKXĐ của phương trình.
+ Quy đồng mẫu rồi khử mẫu.
+ Giải phương trình vừa nhận được.
+ Đối chiếu điều kiện rồi kết luận nghiệm.
*Xét phương trình \(\left( 1 \right)\): \(\dfrac{1}{x} + \dfrac{2}{{x - 2}} = 0\)
ĐKXĐ: \(x \ne 0;x \ne 2\)
Khi đó
\(\begin{array}{l}\dfrac{1}{x} + \dfrac{2}{{x - 2}} = 0 \Leftrightarrow \dfrac{{1\left( {x - 2} \right) + 2x}}{{x\left( {x - 2} \right)}} = 0\\ \Rightarrow 1\left( {x - 2} \right) + 2x = 0 \Leftrightarrow x - 2 + 2x = 0\\ \Leftrightarrow 3x = 2 \Leftrightarrow x = \dfrac{2}{3}\,\left( {TM} \right)\end{array}\)
Vậy phương trình \(\left( 1 \right)\) có nghiệm duy nhất \(x = \dfrac{2}{3}\).
* Xét phương trình \(\left( 2 \right)\): \(\dfrac{{x - 1}}{{x + 2}} - \dfrac{x}{{x - 2}} = \dfrac{{5x - 2}}{{4 - {x^2}}}\)
ĐKXĐ: \(x \ne \pm 2\)
Khi đó
\(\begin{array}{l}\dfrac{{x - 1}}{{x + 2}} - \dfrac{x}{{x - 2}} = \dfrac{{5x - 2}}{{4 - {x^2}}}\\ \Leftrightarrow \dfrac{{x - 1}}{{x + 2}} - \dfrac{x}{{x - 2}} + \dfrac{{5x - 2}}{{{x^2} - 4}} = 0\\ \Leftrightarrow \dfrac{{\left( {x - 1} \right)\left( {x - 2} \right) - x\left( {x + 2} \right) + 5x - 2}}{{\left( {x + 2} \right)\left( {x - 2} \right)}} = 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {x - 2} \right) - x\left( {x + 2} \right) + 5x - 2 = 0\\ \Leftrightarrow {x^2} - 3x + 2 - {x^2} - 2x + 5x - 2 = 0\\ \Leftrightarrow 0x = 0 \Leftrightarrow x \in \mathbb{R}.\end{array}\)
Kết hợp ĐKXĐ ta có phương trình nghiệm đúng với mọi \(x \ne \pm 2\).
Do đó phương trình \(\left( 2 \right)\) có nghiều nghiệm hơn phương trình \(\left( 1 \right)\).
Biết \({x_0}\) là nghiệm nhỏ nhất của phương trình
\(\dfrac{1}{{{x^2} + 4x + 3}} + \dfrac{1}{{{x^2} + 8x + 15}} + \dfrac{1}{{{x^2} + 12x + 35}} + \dfrac{1}{{{x^2} + 16x + 63}} = \dfrac{1}{5}.\) Chọn khẳng định đúng.
-
A.
\({x_0} > 0\)
-
B.
\({x_0} < - 5\)
-
C.
\({x_0} = - 10\)
-
D.
\({x_0} > 5\)
Đáp án : B
Phân tích mẫu thức thành nhân tử rồi sử dụng phương pháp tách hạng tử để giải
\(\dfrac{1}{{\left( {x + a} \right)\left( {x + b} \right)}} = \dfrac{1}{{b - a}}\left( {\dfrac{1}{{x + a}} - \dfrac{1}{{x + b}}} \right),a \ne b\) .
Sau đó, làm theo các bước giải phương trình chứa ẩn ở mẫu:
+ Tìm ĐKXĐ của phương trình.
+ Quy đồng mẫu rồi khử mẫu.
+ Giải phương trình vừa nhận được.
+ Đối chiếu điều kiện rồi kết luận nghiệm.
Phân tích các mẫu thành nhân tử sau đó nhân cả 2 vế của phương trình với 2 ta được:
\(\dfrac{1}{{\left( {x + 1} \right)\left( {x + 3} \right)}} + \dfrac{1}{{\left( {x + 3} \right)\left( {x + 5} \right)}} + \dfrac{1}{{\left( {x + 5} \right)\left( {x + 7} \right)}} + \dfrac{1}{{\left( {x + 7} \right)\left( {x + 9} \right)}} = \dfrac{1}{5} \)
\(\dfrac{2}{{\left( {x + 1} \right)\left( {x + 3} \right)}} + \dfrac{2}{{\left( {x + 3} \right)\left( {x + 5} \right)}} + \dfrac{2}{{\left( {x + 5} \right)\left( {x + 7} \right)}} + \dfrac{2}{{\left( {x + 7} \right)\left( {x + 9} \right)}} = \dfrac{2}{5}\)
ĐKXĐ: $x \ne - 1; - 3; - 5; - 7; - 9$ .
Khi đó:
\( \dfrac{1}{{x + 1}} - \dfrac{1}{{x + 3}} + \dfrac{1}{{x + 3}} - \dfrac{1}{{x + 5}} + \dfrac{1}{{x + 5}} - \dfrac{1}{{x + 7}} + \dfrac{1}{{x + 7}} - \dfrac{1}{{x + 9}} = \dfrac{2}{5} \\\dfrac{1}{{x + 1}} - \dfrac{1}{{x + 9}} = \dfrac{2}{5} \\\dfrac{{1\left( {x + 9} \right) - 1\left( {x + 1} \right)}}{{\left( {x + 1} \right)\left( {x + 9} \right)}} = \dfrac{{2\left( {x + 1} \right)\left( {x + 9} \right)}}{{5\left( {x + 1} \right)\left( {x + 9} \right)}} \\5\left[ {x + 9 - \left( {x + 1} \right)} \right] = 2\left( {x + 1} \right)\left( {x + 9} \right)\\5\left( {x + 9 - x - 1} \right) = 2{x^2} + 20x + 18\\2{x^2} + 20x - 22 = 0\\{x^2} + 10x - 11 = 0\\{x^2} - x + 11x - 11 = 0 \\\left( {x - 1} \right)\left( {x + 11} \right) = 0\)
Suy ra \(x - 1 = 0\) hoặc \(x + 11 = 0\)
hay \(x = 1\left( {TM} \right)\) hoặc \(x = - 11 \left( {TM} \right)\)
Vậy \({x_0} = - 11 < - 5\) .
Hai xe khởi hành cùng một lúc, xe thứ nhất đến sớm hơn xe thứ hai $3$ giờ. Nếu gọi thời gian đi của xe thứ nhất là $x$ giờ thì thời gian đi của xe thứ hai là:
-
A.
\((x - 3)\) giờ
-
B.
\(3x\) giờ
-
C.
\((3 - x)\) giờ
-
D.
\((x + 3)\) giờ
Đáp án : D
Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết.
Vì hai xe khởi hành cùng một lúc, xe thứ nhất đến sớm hơn xe thứ hai $3$ giờ nên thời gian xe thứ hai đi nhiều hơn xe thứ nhất \(3\) giờ.
Nếu thời gian đi của xe thứ nhất là $x$ giờ thì thời gian đi của xe thứ hai là \(x + 3\) giờ.
Một tổ sản xuất theo kế hoạch mỗi ngày phải sản xuất $50$ sản phầm. Khi thực hiện tổ đã sản xuất được $57$ sản phẩm một ngày. Do đó hoàn thành trước kế hoạch $1$ ngày và còn vượt mức $13$ sản phẩm. Hỏi theo kế hoạch tổ phải sản xuất bao nhiêu sản phẩm?
-
A.
\(550\)
-
B.
\(400\)
-
C.
\(600\)
-
D.
\(500\)
Đáp án : D
Giải bài toán năng suất bằng cách lập phương trình
+) Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết.
+) Sau đó dựa vào giả thiết của đề bài để lập phương trình.
+) Giải phương trình rồi so sánh điều kiện để kết luận.
Sử dụng: Năng suất bằng tỉ số giữa khối lượng công việc và thời gian hoàn thành
Gọi tổng sản phẩm tổ phải sản xuất theo kế hoạch là \(x\,\left( {x > 0} \right)\) (sản phẩm)
Thời gian theo kế hoạch là \(\dfrac{x}{{50}}\) (ngày)
Theo thực tế số sản phẩm tổ đã làm là \(x + 13\)(sản phẩm)
Vì thực tế tổ hoàn thành trước kế hoạch \(1\) ngày nên ta có phương trình
\(\dfrac{{x + 13}}{{57}} + 1 = \dfrac{x}{{50}} \\ 50\left( {x + 13} \right) + 2850 = 57x\)
\(7x = 3500 \\x = 500\,\left( {TM} \right)\)
Vậy tổng sản phẩm theo kế hoạch là \(500\) sản phẩm.
Tìm số tự nhiên có bốn chữ số, biết rằng nếu viết thêm chữ số $1$ vào đằng trước ta được số $A$ có năm chữ số, nếu viết them chữ số $4$ vào đằng sau ta được số $B$ có năm chữ số, trong đó $B$ gấp bốn lần $A$ .
-
A.
$6789$
-
B.
$6666$
-
C.
$6699$
-
D.
$9999$
Đáp án : B
Giải theo các bước sau:
+ Lập phương trình: Chọn ẩn và đặt điều kiện; biểu diễn đại lượng chưa biết theo ẩn và đại lượng đã biết; lập phương trình biểu thị mối quan hệ giữa các đại lượng
+ Giải phương trình
+ Đối chiếu điều kiện rồi kết luận
Gọi số phải tìm $\overline {abcd} $ là $x$ . Điều kiện: $x \in N;1000 \le x \le 9999$.
Viết thêm chữ số 1 vào đằng trước ta được
$A = \overline {1abcd} = 10000 + \overline {abcd} = 10000 + x$
Viết thêm chữ số 4 vào đằng sau ta được.
$B = \overline {abcd4} = 10.\overline {abcd} + 4 = 10x + 4$
Theo đề bài $B = 4A$ nên có Phương trình
$10x + 4 = 4\left( {10000 + x} \right)$
Giải phương trình
$10x + 4 = 40000 + 4x$
$\begin{array}{l} \Leftrightarrow \,\,\,\,\,\,\,\,\,\,10x - 4x = 40000 - 4\\ \Leftrightarrow \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,6x = 39996\\ \Leftrightarrow \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = 6666\end{array}$
Giá trị $x = 6666$ thỏa mãn các điều kiện nêu trên. Số phải tìm là $6666$ .
Cho \(a > b\) khi đó
-
A.
\(a - b > 0\)
-
B.
\(a - b < 0\)
-
C.
\(a - b = 0\)
-
D.
\(a - b \le 0\)
Đáp án : A
Sử dụng: Nếu cộng cả hai vế với cùng một số thì bất đẳng thức không đổi chiều.
Từ \(a > b\), cộng \( - b\) vào hai vế ta được \(a - b > b - b,\) tức là \(a - b > 0\).
Ta cũng chỉ ra được rằng : Từ \(a - b > 0\), cộng \(b\) vào hai vế ta được \(a - b + b > 0 + b,\) tức là \(a > b\).
Vì vậy, để chứng minh bất đẳng thức \(a > b\) ta có thể chứng minh bất đẳng thức \(a - b > 0\) , tức là xét hiệu hai vế \(a - b\) rồi chứng minh hiệu đó là số dương.
Cho \(a + 8 < b\). So sánh \(a - 7\) và \(b - 15\)
-
A.
\(a - 7 < b - 15\)
-
B.
\(a - 7 > b - 15\)
-
C.
\(a - 7 \ge b - 15\)
-
D.
\(a - 7 \le b - 15\)
Đáp án : A
Sử dụng tính chất: Cộng cả hai vế với một số thì dấu không đổi để làm xuất hiện \(a - 7\) và \(b - 15\)
Cộng cả hai vế của bất đẳng thức \(a + 8 < b\) với $\left( { - 15} \right)$ ta được
\(a + 8 < b \)
\(a + 8 - 15 < b - 15 \)
\(a - 7 < b - 15\)
Với \(a,b\) bất kỳ. Chọn khẳng định sai.
-
A.
\({a^2} + 5 > 4a\)
-
B.
\({a^2} + 10 < 6a - 1\)
-
C.
\({a^2} + 1 > a\)
-
D.
\(ab - {b^2} \le {a^2}\)
Đáp án : B
Phương pháp xét hiệu.
* ${a^2} + 5 - 4a = {a^2} - 4a + 4 + 1 = {(a - 2)^2} + 1 > 0$ (luôn đúng) nên \({a^2} + 5 > 4a\)
* ${a^2} + 1 - a = {a^2} - 2a.\dfrac{1}{2} + \dfrac{1}{4} + \dfrac{3}{4} = {\left( {a - \dfrac{1}{2}} \right)^2} + \dfrac{3}{4} > 0$ (luôn đúng) nên \({a^2} + 1 > a\)
\(\begin{array}{l}{a^2} + 10 - \left( {6a + 1} \right)\\ = {a^2} - 6a + 10 - 1\\ = {a^2} - 6a + 9\\ = {\left( {a - 3} \right)^2} \ge 0\end{array}\)
Vì \({(a - 3)^2} \ge 0\) (luôn đúng) nên \({a^2} + 10 > 6a + 1\) . Do đó B sai.
* Ta có:
\(\begin{array}{l}{a^2} \ge ab - {b^2} \\ {a^2} - ab + {b^2} \ge 0\\ {a^2} - 2a.\dfrac{b}{2} + \dfrac{{{b^2}}}{4} + \dfrac{{3{b^2}}}{4} \ge 0 \\ {\left( {a - \dfrac{b}{2}} \right)^2} + \dfrac{{3{b^2}}}{4} \ge 0\end{array}\)
Vì \({\left( {a - \dfrac{b}{2}} \right)^2} + \dfrac{{3{b^2}}}{4} \ge 0\) (luôn đúng) nên \({a^2} \ge ab - {b^2}\).
Cho $a,b$ bất kì. Chọn câu đúng.
-
A.
\(\dfrac{{{a^2} + {b^2}}}{2} < ab\)
-
B.
\(\dfrac{{{a^2} + {b^2}}}{2} \le ab\)
-
C.
\(\dfrac{{{a^2} + {b^2}}}{2} \ge ab\)
-
D.
\(\dfrac{{{a^2} + {b^2}}}{2} > ab\)
Đáp án : C
+) Xét hiệu \(P = \dfrac{{{a^2} + {b^2}}}{2} - ab\)
+) Đưa về hằng đẳng thức và đánh giá.
Xét hiệu \(P = \dfrac{{{a^2} + {b^2}}}{2} - ab\) \( = \dfrac{{{a^2} + {b^2} - 2ab}}{2}\) \( = \dfrac{{{{\left( {a - b} \right)}^2}}}{2} \ge 0\) (luôn đúng với mọi \(a,\,b\) )
Nên \(\dfrac{{{a^2} + {b^2}}}{2} \ge ab\)
Bất đẳng thức nào sau đây đúng với mọi \(a > 0,b > 0:\)
-
A.
\({a^3} + {b^3} - a{b^2} - {a^2}b < 0\)
-
B.
\({a^3} + {b^3} - a{b^2} - {a^2}b \ge 0\)
-
C.
\({a^3} + {b^3} - a{b^2} - {a^2}b \le 0\)
-
D.
\({a^3} + {b^3} - a{b^2} - {a^2}b > 0\)
Đáp án : B
+ Phân tích vế trái thành nhân tử và đánh giá theo điều kiện của \(a,\,b\).
Ta có ${a^3} + {b^3} - a{b^2} - {a^2}b = {a^2}(a - b) - {b^2}(a - b)$
$ = {(a - b)^2}(a + b) \ge 0$ ( vì \({\left( {a - b} \right)^2} \ge 0\,\) với mọi \(a,b\) và \(a + b > 0\) với \(a > 0,b > 0\)).
Học sinh có thể nhầm đáp án D vì không xét tới nếu \(a = b\) thì \({a^3} + {b^3} - a{b^2} - {a^2}b = {\left( {a - b} \right)^2}\left( {a + b} \right) = 0\) nên D sai.
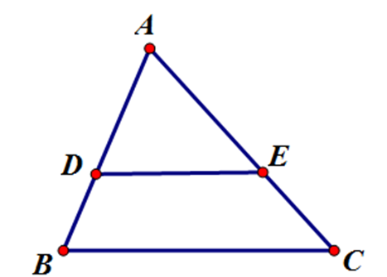
Hãy chọn câu sai. Cho hình vẽ với $AB<AC$:

-
A.
\(\dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}} \Rightarrow DE//BC\).
-
B.
\(\dfrac{{AD}}{{DB}} = \dfrac{{AE}}{{EC}} \Rightarrow DE//BC\).
-
C.
\(\dfrac{{AB}}{{DB}} = \dfrac{{AC}}{{EC}} \Rightarrow DE//BC\).
-
D.
\(\dfrac{{AD}}{{DE}} = \dfrac{{AE}}{{ED}} \Rightarrow DE//BC\).
Đáp án : D
Theo định lý đảo của định lý Ta-lét: Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Nên D sai.
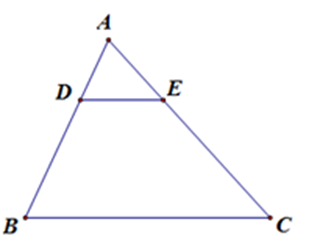
Cho hình vẽ, trong đó $DE{\rm{//}}BC$, $AD = 12,\,\,DB = 18,\,\,CE = 30$. Độ dài $AC$ bằng:

-
A.
\(20\)
-
B.
\(\dfrac{{18}}{{25}}\)
-
C.
\(50\)
-
D.
\(45\)
Đáp án : C
Sử dụng định lý Ta-lét tính \(AE\) từ đó tính \(AC\) .
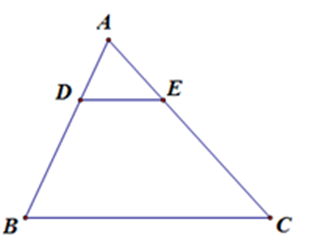
Vì $DE{\rm{//}}BC$, theo định lý Ta-lét ta có \(\dfrac{{AD}}{{BD}} = \dfrac{{AE}}{{EC}} \Leftrightarrow \dfrac{{12}}{{18}} = \dfrac{{AE}}{{30}}\)\( \Rightarrow EA = \dfrac{{30.12}}{{18}} = 20\,cm\)
Nên \(AC = AE + EC = 50\,cm\)
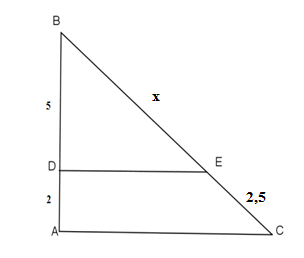
Chọn câu trả lời đúng: Cho hình bên, biết \(DE{\rm{//}}AC\), tìm \(x\) :

-
A.
\(x = 6,5\)
-
B.
\(x = 6,25\)
-
C.
\(x = 5\)
-
D.
\(x = 8\)\(\)
Đáp án : B
Bước 1: Áp dụng định lý Talet để lập được tỉ lệ thức phù hợp
Bước 2: Biến đổi tỉ lệ thức để tìm ra giá trị $x$ .
Vì \(DE{\rm{//}}AC\), áp dụng định lý Talet, ta có:
\(\dfrac{{BD}}{{BA}} = \dfrac{{BE}}{{BC}}\)\( \Rightarrow \dfrac{{BD}}{{BD + DA}} = \dfrac{{BE}}{{BE + EC}}\)\( \Rightarrow \dfrac{5}{{5 + 2}} = \dfrac{x}{{x + 2,5}} \)\(\Rightarrow \dfrac{x}{{x + 2,5}} = \dfrac{5}{7} \)\( \Rightarrow 7x = 5x + 12,5 \)\(\Rightarrow x = 6,25. \)
Cho tứ giác \(ABCD\), lấy bất kỳ \(E \in BD\) . Qua \(E\) vẽ \(EF\) song song với \(AD\)( \(F\) thuộc \(AB\)), vẽ \(EG\) song song với \(DC\)(\(G\) thuộc\(BC\)). Chọn khẳng định sai.
-
A.
\(\dfrac{{BE}}{{ED}} = \dfrac{{BG}}{{GC}}\)
-
B.
\(\dfrac{{BF}}{{FA}} = \dfrac{{BG}}{{GC}}\)
-
C.
\(FG{\rm{//}}AC\)
-
D.
\(FG{\rm{//}}AD\)\(\)
Đáp án : D
Sử dụng định lý Ta-lét và định lý Ta-lét đảo để suy ra các hệ thức đúng.
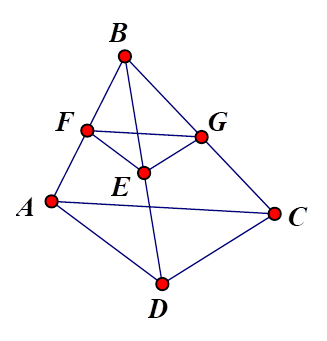
Áp dụng định lí Ta-lét trong \(\Delta ABD\) với \(EF{\rm{//}}AD\), ta có \(\dfrac{{BE}}{{ED}} = \dfrac{{BF}}{{FA}}\). (1)
Áp dụng định lí Ta-lét trong\(\Delta BDC\) với \(EG{\rm{//}}DC\), ta có \(\dfrac{{BE}}{{ED}} = \dfrac{{BG}}{{GC}}\). (2)
Từ (1) và (2) suy ra\(\dfrac{{BF}}{{FA}} = \dfrac{{BG}}{{GC}}\), do đó \(FG{\rm{//}}AC\)(định lí Ta-lét đảo).
Vậy A, B, C đúng, D sai.
Cho tam giác ABC có AM là đường trung tuyến, N là điểm trên đoạn thẳng AM. Gọi D là giao điểm của CN và AB, E là giao điểm của BN và AC. Chọn khẳng định đúng nhất.
-
A.
\(DE{\rm{//}}BC\)
-
B.
\(\dfrac{{AD}}{{BD}} = \dfrac{{AE}}{{CE}}\)
-
C.
Cả A, B đều đúng
-
D.
Cả A, B đều sai\(\)
Đáp án : C
Bước 1: Vẽ thêm đường thẳng song song để hình thành các cặp đoạn thẳng tỉ lệ.
Bước 2: Áp dụng định lý Talet và tính chất bắc cầu để tìm ra tỉ lệ thức cần chứng minh
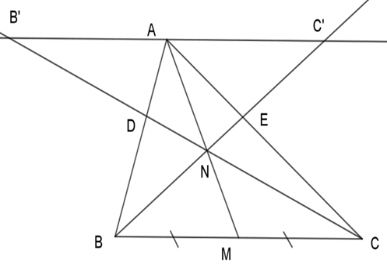
Kẻ đường thẳng đi qua $A$ song song với $BC$ lần lượt cắt $CD$ và $BE$ kéo dài tại \(B'\) và \(C'\).
Vì M là trung điểm của $BC$ nên \(BM = MC\).
Vì \(AB'{\rm{//}}MC\), áp dụng định lý Talet ta có:
\(\dfrac{{AN}}{{NM}} = \dfrac{{AB'}}{{MC}}\) (1)\(\)
Vì \(AC'{\rm{//}}\,BM\), áp dụng định lý Talet ta có:
\(\dfrac{{AN}}{{NM}} = \dfrac{{AC'}}{{BM}}\) (2)
Từ (1) và (2) ta có: \(\dfrac{{AB'}}{{MC}} = \dfrac{{AC'}}{{BM}}\)
Ta có $M$ là trung điểm của $BC$ \( \Rightarrow \)\(BM = MC\)\( \Rightarrow \)\(AB' = AC'\) (*)
Vì \(AB'{\rm{//}}\,BC\), áp dụng định lý Talet ta có:
\(\dfrac{{AD}}{{DB}} = \dfrac{{AB'}}{{BC}}\) (**)
Vì \(AC'{\rm{//}}\,BC\), áp dụng định lý Talet ta có:
\(\dfrac{{AE}}{{EC}} = \dfrac{{AC'}}{{BC}}\) (***)
Từ (*), (**) và (***) ta có:
\(\dfrac{{AD}}{{DB}} = \dfrac{{AB'}}{{BC}} = \dfrac{{AE}}{{EC}} = \dfrac{{AC'}}{{BC}}\)
\( \Rightarrow \dfrac{{AD}}{{DB}} = \dfrac{{AE}}{{EC}}\)\( \Leftrightarrow \dfrac{{AD}}{{BD}} = \dfrac{{AE}}{{CE}}\) hay \(DE{\rm{//}}BC\)
Hãy chọn câu đúng. Nếu $\Delta ABC$ và $\Delta DEF$ có $\widehat B = \widehat {D;}\,\dfrac{{BA}}{{BC}} = \dfrac{{DE}}{{DF}}$ thì:
-
A.
$\Delta ABC$ đồng dạng với $\Delta DEF$
-
B.
$\Delta ABC$ đồng dạng với $\Delta EDF$
-
C.
$\Delta BCA$ đồng dạng với $\Delta DEF$
-
D.
$\Delta ABC$ đồng dạng với $\Delta FDE$
Đáp án : B
$\Delta ABC$ và $\Delta DEF$ có $\widehat B = \widehat {D;}\,\dfrac{{BA}}{{BC}} = \dfrac{{DE}}{{DF}}$ thì $\Delta ABC$ đồng dạng với $\Delta EDF$
Các em cần ghi đúng thứ tự các cạnh tỉ lệ và các góc tương ứng bằng nhau.
Cho $\Delta DHE \backsim\Delta ABC$ với tỉ số đồng dạng $\dfrac{2}{3}$. Có bao nhiêu khẳng định đúng trong các khẳng định sau:
(I) Tỉ số hai đường cao tương ứng của $\Delta DHE$ và $\Delta ABC$ là $\dfrac{2}{3}$.
(II) Tỉ số hai đường cao tương ứng của $\Delta ABC$ và $\Delta DHE$ là $\dfrac{2}{3}$.
(III) Tỉ số diện tích của $\Delta ABC$ và $\Delta DHE$ là $\dfrac{2}{3}$.
(IV) Tỉ số diện tích của $\Delta DHE$ và $\Delta ABC$ là $\dfrac{4}{9}$.
-
A.
\(2\)
-
B.
\(1\)
-
C.
\(3\)
-
D.
\(4\)
Đáp án : A
Sử dụng tỉ số đường cao, tỉ số diện tích của hai tam giác đồng dạng.
Nếu hai tam giác đồng dạng thì:
+ Tỉ số hai đường cao tương ứng bằng tỉ số đồng dạng;
+ Tỉ số hai diện tích bằng bình phương tỉ số đồng dạng.
Vì $\Delta DHE\backsim\Delta ABC$ với tỉ số đồng dạng $\dfrac{2}{3}$ nên tỉ số hai đường cao tương ứng của $\Delta DHE$ và $\Delta ABC$ là $\dfrac{2}{3}$ và tỉ số diện tích của $\Delta DHE$ và $\Delta ABC$ là ${\left( {\dfrac{2}{3}} \right)^2} = \dfrac{4}{9}$
Do đó (I) và (IV) đúng, (II) và (III) sai.
Hãy chọn câu đúng. Hình hộp chữ nhật có ba kích thước lần lượt là: $a$, $2a$, $\dfrac{a}{2}$ thể tích của hình hộp chữ nhật đó là:
-
A.
${a^2}$
-
B.
$4{a^2}$
-
C.
$2{a^4}$
-
D.
${a^3}$
Đáp án : D
Sử dụng công thức thể tích của hình hộp chữ nhật $V = abc$ ($a,b,c$ là các kích thước của hình hộp chữ nhật)
Thể tích của hình hộp chữ nhật là \(V = a.2a.\dfrac{a}{2} = {a^3}\) (đvtt)
Các em cần nhớ đúng công thức khi tính toán.
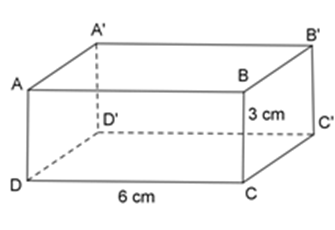
Các kích thước của hình hộp chữ nhật \(ABC{\rm{D}}.A'B'C'D'\) là $DC = 6cm$ , $CB = 3cm$ . Hỏi độ dài của \(A'B'\) và $AD$ là bao nhiêu $cm$ ?

-
A.
$3\,cm$ và $6\,cm$
-
B.
$6\,cm$ và $9\,cm$
-
C.
$6\,cm$ và $3\,cm$
-
D.
$9\,cm$ và $6\,cm$
Đáp án : C
Từ kiến thức lý thuyết về hình hộp chữ nhật kết hợp với tính chất của hình chữ nhật để giải bài toán và chọn đáp án đúng.
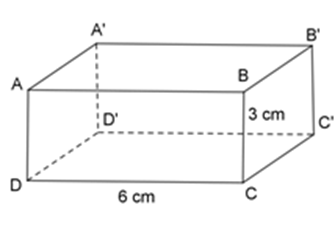
Vì \(ABC{\rm{D}}.A'B'C'D'\) là hình hộp chữ nhật nên $ABCD,$ \(ABB'A'\) là hình chữ nhật.
Xét hình chữ nhật $ABCD$ có: $AD = BC = 3cm,DC = AB = 6cm$
Xét hình chữ nhật \(ABB'A'\) có: \(A'B' = AB = 6\;cm\)
Vậy \(A'B'\) và $AD$ lần lượt dài $6 cm$ và $3 cm.$
- Học sinh cần viết đúng các cặp cạnh bằng nhau.
Thể tích của hình chóp tứ giác đều có chiều cao $6$ cm, cạnh đáy $4$ cm là
-
A.
$32\,c{m^3}$
-
B.
$24\,c{m^3}$
-
C.
$144\,c{m^3}$
-
D.
$96\,c{m^3}$
Đáp án : A
Sử dụng công thức tính thể tích hình chóp đều
Thể tích của hình chóp đều bằng $\dfrac{1}{3}$ diện tích đáy nhân với chiều cao $V = \dfrac{1}{3}S.h$
( $S$ là diện tích đáy, $h$ là chiều cao)
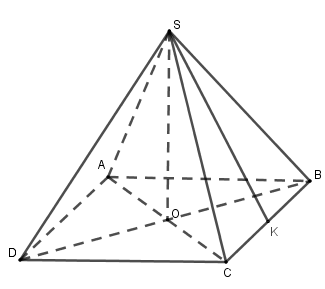
Đáy của chóp tứ giác đều là hình vuông nên diện tích đáy là \(S = {4^2} = 16\,c{m^2}\) .
Thể tích cần tìm là \(V = \dfrac{1}{3}.6.16 = 32\,c{m^3}\) .
Phương trình \({x^2} + x = 0\) có số nghiệm là
-
A.
1 nghiệm
-
B.
2 nghiệm
-
C.
vô nghiệm
-
D.
vô số nghiệm
Đáp án : B
Vế trái đặt nhân tử chung rồi đưa phương trình về dạng phương trình tích $A.B=0$ thì $A = 0$ hoặc $B = 0$
Từ đó tìm $x$.
\({x^2} + x = 0 \\ x\left( {x + 1} \right) = 0 \)
Suy ra \(x = 0\) hoặc \(x + 1 = 0\)
hay \(x = 0\) hoặc \(x = - 1\)
Vậy phương trình có 2 nghiệm $x=-1;x=0$
Phương trình \(\dfrac{x}{{x - 5}} - \dfrac{3}{{x - 2}} = 1\) có nghiệm là
-
A.
\(x = - \dfrac{1}{2}\)
-
B.
\(x = \dfrac{5}{2}\)
-
C.
\(x = \dfrac{1}{2}\)
-
D.
\(x = - \dfrac{5}{2}\)
Đáp án : D
+ Tìm ĐKXĐ của phương trình.
+ Quy đồng mẫu rồi khử mẫu.
+ Giải phương trình vừa nhận được.
+ Đối chiếu điều kiện rồi kết luận nghiệm.
ĐKXĐ: \(x \ne 2;x \ne 5\)
\(\dfrac{x}{{x - 5}} - \dfrac{3}{{x - 2}} = 1\,\\\dfrac{x}{{x - 5}} - \dfrac{3}{{x - 2}} - 1 = 0\\\dfrac{{x\left( {x - 2} \right) - 3\left( {x - 5} \right) - 1\left( {x - 2} \right)\left( {x - 5} \right)}}{{\left( {x - 2} \right)\left( {x - 5} \right)}} = 0\\x\left( {x - 2} \right) - 3\left( {x - 5} \right) - 1\left( {x - 2} \right)\left( {x - 5} \right) = 0\\{x^2} - 2x - 3x + 15 - {x^2} + 7x - 10 = 0\\2x + 5 = 0\\2x = - 5 \\x = - \dfrac{5}{2}\left( {tmdk} \right).\)
Phương trình \(\dfrac{{x - 1}}{2} + \dfrac{{x - 1}}{3} - \dfrac{{x - 1}}{6} = 2\) có tập nghiệm là
-
A.
\(S = \left\{ {0;1} \right\}\)
-
B.
\(S = \left\{ 4 \right\}\)
-
C.
\(S = \emptyset \)
-
D.
\(S = \mathbb{R}\)
Đáp án : B
Vế trái đặt nhân tử chung rồi đưa phương trình về dạng phương trình bậc nhất một ẩn
\(\begin{array}{l}\dfrac{{x - 1}}{2} + \dfrac{{x - 1}}{3} - \dfrac{{x - 1}}{6} = 2\\ \dfrac{{1}}{2} (x-1) + \dfrac{1}{3}(x-1) - \dfrac{1}{6}(x-1) = 2\\\\\left( {x - 1} \right)\left( {\dfrac{1}{2} + \dfrac{1}{3} - \dfrac{1}{6}} \right) = 2\\\left( {x - 1} \right)\dfrac{4}{6} = 2\\x - 1= 3\\x= 4\\S = \left\{ 4 \right\}\end{array}\)
Tích các nghiệm của phương trình: \(\left( {{x^2} - 3x + 3} \right)\left( {{x^2} - 2x + 3} \right) = 2{x^2}\) là
-
A.
\( - 2\)
-
B.
\(2\)
-
C.
\(4\)
-
D.
\(3\)
Đáp án : D
+ Nhận thấy 0 không phải là nghiệm của phương trình nên ta chia cả hai vế của phương trình cho \({x^2} \ne 0\) .
+ Sau đó biến đổi phương trình để làm xuất hiện nhóm hạng tử giống nhau, đặt nhóm hạng tử giống nhau bằng ẩn mới, thay vào phương trình đã cho để được phương trình theo ẩn mới.
+ Giải phương trình theo ẩn mới
+ Thay giá trị vừa tìm được của ẩn mới vào biểu thức đặt ẩn để tìm ẩn ban đầu.
Nhận thấy \(x = 0\) không là nghiệm của phương trình nên chia hai vế của phương trình cho \({x^2} \ne 0\) ta được:
\(\dfrac{{{x^2} - 3x + 3}}{x}.\dfrac{{{x^2} - 2x + 3}}{x} = 2 \\ \left( {x + \dfrac{3}{x} - 3} \right)\left( {x + \dfrac{3}{x} - 2} \right) = 2\)
Đặt \(t = x + \dfrac{3}{x} - 3\) , ta có:
\(t\left( {t + 1} \right) = 2 \\ {t^2} + t - 2 = 0\\ \left( {t - 1} \right)\left( {t + 2} \right) = 0\)
Suy ra \(t – 1 = 0\) hoặc \(t + 2 = 0\)
Tức là \(t = 1\) hoặc \(t = - 2\)
Với \(t = 1\), ta có:
\(x + \dfrac{3}{x} - 3 = 1 \\ {x^2} - 4x + 3 = 0 \\ \left( {x - 1} \right)\left( {x - 3} \right) = 0 \)
Suy ra \(x - 1 = 0\) hoặc \(x - 3 = 0\)
tức là \(x = 1\) hoặc \(x = 3\)
Với \(t = - 2\), ta có:
\( x + \dfrac{3}{x} - 3 = - 2 \\ {x^2} - x + 3 = 0 \\ {\left( {x - \dfrac{1}{2}} \right)^2} + \dfrac{{11}}{4} = 0 (VN)\)
Vậy phương trình có tập nghiệm là \(S = \left\{ {1;3} \right\}\)
Tích các nghiệm của phương trình là \(1.3 = 3.\)
Nghiệm của bất phương trình $7(3x + 5) > 0$ là:
-
A.
$x > \dfrac{3}{5}$
-
B.
$x \le - \dfrac{5}{3}$
-
C.
$x \ge - \dfrac{5}{3}$
-
D.
$x > - \dfrac{5}{3}$.
Đáp án : D
Giải bất phương trình tìm nghiệm phù hợp bằng cách dùng qui tắc nhân và qui tắc chuyển vế
Vì \(7 > 0\) nên \(7\left( {3x + 5} \right) \ge 3 \Leftrightarrow 3x + 5 > 0 \Leftrightarrow 3x > - 5 \Leftrightarrow x > - \dfrac{5}{3}.\)
Chuyển vế phải đổi dấu, chia cho một số dương thì bất phương trình không đổi chiều
Với giá trị nào của $m$ thì bất phương trình $m(2x + 1) < 8$ là bất phương trình bậc nhất một ẩn?
-
A.
$m \ne 1$
-
B.
$m \ne - \dfrac{1}{3}$
-
C.
$m \ne 0$
-
D.
$m \ne 8$.
Đáp án : C
Dựa vào định nghĩa bất phương trình bậc nhất một ẩn.
Bất phương trình dạng \(ax + b > 0\) (hoặc \(ax + b < 0,ax + b \ge 0,ax + b \le 0\)) trong đó \(a\) và \(b\) là hai số đã cho, \(a \ne 0\), gọi là bất phương trình bậc nhất một ẩn.
Ta có: $m(2x + 1) < 8 \Leftrightarrow 2mx + m < 8 \Leftrightarrow 2mx + m - 8 < 0$.
Vậy để bất phương trình \(m\left( {2x + 1} \right) < 8\) là bất phương trình bậc nhất 1 ẩn thì \(2mx + m - 8 < 0\) là bất phương trình bậc nhất một ẩn.
Theo định nghĩa bất phương trình bậc nhất một ẩn thì \(a \ne 0\) hay \(2m \ne 0\) $\Leftrightarrow m \ne 0$
Số nguyên nhỏ nhất thỏa mãn bất phương trình $x(5x + 1) + 4(x + 3) > 5{x^2}$ là
-
A.
$x = - 3$
-
B.
$x = 0$
-
C.
\(x = - 1\)
-
D.
\(x = - 2\).
Đáp án : D
Nhân đơn thức với đa thức
Áp dụng quy tắc chuyển vế, nhân với một số âm hoặc dương.
\(\begin{array}{l}\;x(5x + 1) + 4(x + 3) > 5{x^2}\\ \Leftrightarrow 5{x^2} + x + 4x + 12 > 5{x^2}\\ \Leftrightarrow 5x > - 12\\ \Leftrightarrow x > \dfrac{{ - 12}}{5}\end{array}\)
Vậy nghiệm của bất phương trình là \(x > - \dfrac{{12}}{5}.\)
Số nguyên lớn nhất thỏa mãn bất phương trình là \(x = - 2.\)
Tích các nghiệm của phương trình $|{x^2} + 2x - 1| = 2$ là
-
A.
\(3\)
-
B.
\( - 3\)
-
C.
\(1\)
-
D.
\( - 1\).
Đáp án : A
Sử dụng: Với $B(x) \ge 0$ thì
\(\left| {A(x)} \right| = B(x) \Rightarrow \left[ \begin{array}{l}A(x) = B(x)\\A(x) = - B(x)\end{array} \right.\)
\(\;\;\left| {{x^2} + 2x - 1} \right| = 2 \Leftrightarrow \left[ \begin{array}{l}{x^2} + 2x - 1 = 2\\{x^2} + 2x - 1 = - 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{x^2} + 2x - 3 = 0\\{x^2} + 2x + 1 = 0\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}{x^2} + 3x - x - 3 = 0\\{(x + 1)^2} = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x(x + 3) - (x + 3) = 0\\x + 1 = 0\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}(x + 3)(x - 1) = 0\\x = - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x + 3 = 0\\x - 1 = 0\\x = - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 3\\x = 1\\x = - 1\end{array} \right..\)
Vậy nghiệm của phương trình là $x{\rm{ }} = - 3;{\rm{ }}x = \pm 1.$
Tích các nghiệm của phương trình là \(\left( { - 3} \right).1.\left( { - 1} \right) = 3.\)
Giải phương trình \({\left| {x - 3y} \right|^{2017}} + {\left| {y + 4} \right|^{2018}} = 0\) ta được nghiệm \(\left( {x;y} \right)\). Khi đó \(y - x\) bằng
-
A.
\( - 16\)
-
B.
\( - 8\)
-
C.
\(16\)
-
D.
\(8\).
Đáp án : D
Vận dụng tính chất không âm của giá trị tuyệt đối dẫn đến phương pháp bất đẳng thức.
* Nhận xét: Tổng của các số không âm là một số không âm và tổng đó bằng 0 khi và chỉ khi các số hạng của tổng đồng thời bằng 0.
* Cách giải chung: \(\left| A \right| + \left| B \right| = 0\)
Bước1: Đánh giá: \(\left. \begin{array}{l}\left| A \right| \ge 0\\\left| B \right| \ge 0\end{array} \right\} \Rightarrow \left| A \right| + \left| B \right| \ge 0\)
Bước 2: Khẳng định: \(\left| A \right| + \left| B \right| = 0\)\( \Leftrightarrow \left\{ \begin{array}{l}A = 0\\B = 0\end{array} \right.\)
\({\left| {x - 3y} \right|^{2017}} + {\left| {y + 4} \right|^{2018}} = 0\)
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}\left| {x - 3y} \right| \ge 0\\\left| {y + 4} \right| \ge 0\end{array} \right\} \Rightarrow {\left| {x - 3y} \right|^{2017}} + {\left| {y + 4} \right|^{2018}} \ge 0\\ \Rightarrow {\left| {x - 3y} \right|^{2017}} + {\left| {y + 4} \right|^{2018}} = 0 \Leftrightarrow \left\{ \begin{array}{l}x - 3y = 0\\y + 4 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x - 3.( - 4) = 0\\y = - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 12\\y = - 4\end{array} \right.\end{array}\)
Vậy nghiệm của phương trình là $x = - 12$ và $y = - 4.$
Suy ra \(y - x = - 4 - \left( { - 12} \right) = 8.\)
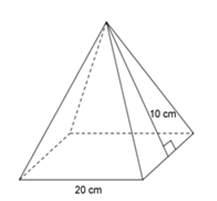
Tính diện tích toàn phần hình chóp tứ giác đều dưới đây:

-
A.
\(600\;c{m^2}\)
-
B.
\(700\;c{m^2}\)
-
C.
\(800\;c{m^2}\)
-
D.
\(900\;c{m^2}\)
Đáp án : C
- Vận dụng công thức tính diện tích toàn phần của hình chóp đều.
\({S_{tp}} = {S_{xq}} + {S_đ}.\)
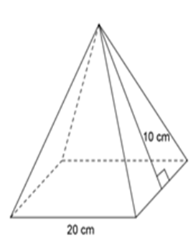
Mỗi mặt bên của hình chóp là tam giác có chiều cao 10 cm và cạnh đáy 20 cm.
Diện tích một mặt bên của hình chóp là $\dfrac{1}{2}.10.20=100\, (cm^2)$
Diện tích xung quanh hình chóp là $S_{xq}=4.100=400\, (cm^2)$
$S_{tp} = S_{xq} + S_{đáy} =$ \(400 + 20.20 = 800\;c{m^2}\)
- Học sinh cần ghi nhớ công thức tính diện tích toàn phần của hình chóp đều.
- Học sinh cẩn thận trong tính toán đại số.
>> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
 |
 |
 |
 |
 |
 |










Danh sách bình luận