Đề kiểm tra học kì 2 Toán 8 - Đề số 3
Đề bài
Chọn khẳng định đúng.
-
A.
3 là nghiệm của phương trình \({x^2} - 9 = 0\)
-
B.
\(\left\{ 3 \right\}\) là tập nghiệm của phương trình \({x^2} - 9 = 0\)
-
C.
Tập nghiệm của phương trình \((x + 3)(x - 3) = {x^2} - 9\) là \(\mathbb{Q}\)
-
D.
\(x = 2\) là nghiệm duy nhất của phương trình \({x^2} - 4 = 0\) .
Phương trình \(2x - 3 = 12 - 3x\) có bao nhiêu nghiệm?
-
A.
\(0\)
-
B.
\(1\)
-
C.
\(2\)
-
D.
Vô số nghiệm
Tính tổng các nghiệm của phương trình \(\left| {3x + 6} \right| - 2 = 4\), biết phương trình có hai nghiệm phân biệt.
-
A.
$0$
-
B.
$10$
-
C.
$4$
-
D.
$ - 4$
Chọn khẳng định đúng.
-
A.
Phương trình \(8x\left( {3x - 5} \right) = 6\left( {3x - 5} \right)\)có hai nghiệm trái dấu
-
B.
Phương trình \(8x\left( {3x - 5} \right) = 6\left( {3x - 5} \right)\)có hai nghiệm cùng dương
-
C.
Phương trình \(8x\left( {3x - 5} \right) = 6\left( {3x - 5} \right)\)có hai nghiệm cùng âm
-
D.
Phương trình \(8x\left( {3x - 5} \right) = 6\left( {3x - 5} \right)\)có một nghiệm duy nhất
Biết rằng phương trình \({\left( {{x^2} - 1} \right)^2} = 4x + 1\) có nghiệm lớn nhất là \({x_0}\) . Chọn hẳng định đúng.
-
A.
\({x_0} = 3\)
-
B.
\({x_0} < 2\)
-
C.
\({x_0} > 1\)
-
D.
\({x_0} < 0\)
Hãy chọn câu đúng. Điều kiện xác định của phương trình \(\dfrac{1}{{x - 2}} + 3 = \dfrac{{3 - x}}{{x - 2}}\) là
-
A.
\(x \ne 3\)
-
B.
\(x \ne 2\)
-
C.
\(x \ne - 3\)
-
D.
\(x \ne - 2\)
Cho hai biểu thức : \(A = 1 + \dfrac{1}{{2 + x}}\) và \(B = \dfrac{{12}}{{{x^3} + 8}}\) . Tìm $x$ sao cho \(A = B\) .
-
A.
\(x = 0\)
-
B.
\(x = 1\)
-
C.
\(x = - 1\)
-
D.
Cả A và B.
Hai xe khởi hành cùng một lúc, xe thứ nhất đến sớm hơn xe thứ hai $3$ giờ. Nếu gọi thời gian đi của xe thứ nhất là $x$ giờ thì thời gian đi của xe thứ hai là:
-
A.
\((x - 3)\) giờ
-
B.
\(3x\) giờ
-
C.
\((3 - x)\) giờ
-
D.
\((x + 3)\) giờ
Một đội máy cày dự định cày $40$ ha ruộng $1$ ngày. Do sự cố gắng, đội đã cày được $52$ ha mỗi ngày. Vì vậy, chẳng những đội đã hoàn thành sớm hơn $2$ ngày mà còn cày vượt mức được $4$ ha nữa. Tính diện tích ruộng đội phải cày theo dự định.
-
A.
\(300\) ha
-
B.
\(630\) ha
-
C.
\(420\) ha
-
D.
\(360\) ha
Trong tháng Giêng hai tổ công nhân may được $800$ chiếc áo. Tháng Hai, tổ $1$ vượt mức $15\% $ , tổ hai vượt mức $20\% $ do đó cả hai tổ sản xuất được $945$ cái áo. Tính xem trong tháng đầu, tổ \(1\) may được bao nhiêu chiếc áo?
-
A.
\(300\)
-
B.
\(500\)
-
C.
\(400\)
-
D.
\(600\)
So sánh $m$ và $n$ biết $m-\dfrac{1}{2} = n$
-
A.
\(m < n\)
-
B.
\(m = n\)
-
C.
\(m \le n\)
-
D.
\(m > n\)
Với \(a,b\) bất kỳ. Chọn khẳng định sai.
-
A.
\({a^2} + 5 > 4a\)
-
B.
\({a^2} + 10 < 6a - 1\)
-
C.
\({a^2} + 1 > a\)
-
D.
\(ab - {b^2} \le {a^2}\)
Cho \(x + y > 1.\) Chọn khẳng định đúng
-
A.
\({x^2} + {y^2} > \dfrac{1}{2}\)
-
B.
\({x^2} + {y^2} < \dfrac{1}{2}\)
-
C.
\({x^2} + {y^2} = \dfrac{1}{2}\)
-
D.
\({x^2} + {y^2} \le \dfrac{1}{2}\)
Biểu diễn tập nghiệm của bất phương trình \(x \ge 8\) trên trục số, ta được
-
A.

-
B.

-
C.

-
D.
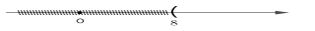
Số nguyên lớn nhất thỏa mãn bất phương trình \(\dfrac{{1987 - x}}{{15}} + \dfrac{{1988 - x}}{{16}} + \dfrac{{27 + x}}{{1999}} + \dfrac{{28 + x}}{{2000}} > 4\) là
-
A.
$x > 1972$
-
B.
$x < 1972$
-
C.
$x < 1973$
-
D.
$x < 1297$
Nghiệm nhỏ nhất của phương trình \(\left| {2 + 3x} \right| = \left| {4x - 3} \right|\) là
-
A.
\(\dfrac{1}{7}\)
-
B.
\(5\)
-
C.
\( - \dfrac{1}{7}\)
-
D.
\( - 5\)
Cho hai phương trình \(4\left| {2x - 1} \right| + 3 = 15\,\,\,\left( 1 \right)\) và \(\left| {7x + 1} \right| - \left| {5x + 6} \right| = 0\,\left( 2 \right)\). Kết luận nào sau đây là đúng.
-
A.
Phương trình \(\left( 1 \right)\) có nhiều nghiệm hơn phương trình \(\left( 2 \right)\)
-
B.
Phương trình \(\left( 1 \right)\) có ít nghiệm hơn phương trình \(\left( 2 \right)\)
-
C.
Cả hai phương trình đều có hai nghiệm phân biệt
-
D.
Cả hai phương trình đều vô số nghiệm
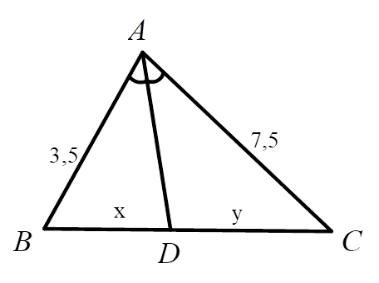
Hãy chọn câu đúng. Tỉ số \(\dfrac{x}{y}\) của các đoạn thẳng trong hình vẽ, biết rằng các số trên hình cùng đơn vị đo là $cm$ .
-
A.
\(\dfrac{7}{{15}}\)
-
B.
\(\dfrac{1}{7}\)
-
C.
\(\dfrac{{15}}{7}\)
-
D.
\(\dfrac{1}{{15}}\)
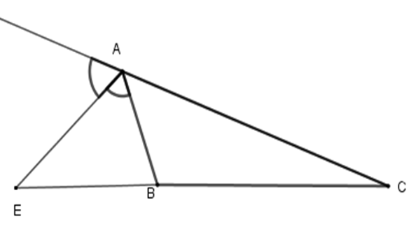
Cho \(\Delta ABC\), \(AE\) là phân giác ngoài của góc A. Hãy chọn câu đúng:
-
A.
\(\dfrac{{AB}}{{AE}} = \dfrac{{BE}}{{CE}}\).
-
B.
\(\dfrac{{AE}}{{AC}} = \dfrac{{BE}}{{CE}}\).
-
C.
\(\dfrac{{AB}}{{AC}} = \dfrac{{CE}}{{BE}}\).
-
D.
\(\dfrac{{AB}}{{AC}} = \dfrac{{BE}}{{CE}}\).
Nếu tam giác $ABC$ có $MN$ // $BC$ (với \(M\in AB, N\in AC)\) thì
-
A.
\({\rm{\Delta }}AMN\) đồng dạng với \({\rm{\Delta }}ACB\).
-
B.
\({\rm{\Delta }}ABC\) đồng dạng với \({\rm{\Delta }}MNA\).
-
C.
\({\rm{\Delta }}AMN\) đồng dạng với \({\rm{\Delta }}ABC\).
-
D.
\({\rm{\Delta }}ABC\) đồng dạng với \({\rm{\Delta }}ANM\).
Một tam giác có cạnh nhỏ nhất bằng $8$ , hai cạnh còn lại bằng $x$ và $y$ \(\left( {x < y} \right).\) Một tam giác khác có cạnh lớn nhất bằng $27$ , hai cạnh còn lại cũng bằng $x$ và $y$ . Tính $x$ và $y$ để hai tam giác đó đồng dạng.
-
A.
$x = 5;\,y = 10$.
-
B.
$x = 6;\,y = 12$
-
C.
$x = 12;\,y = 18$
-
D.
$x = 6;\,y = 18$
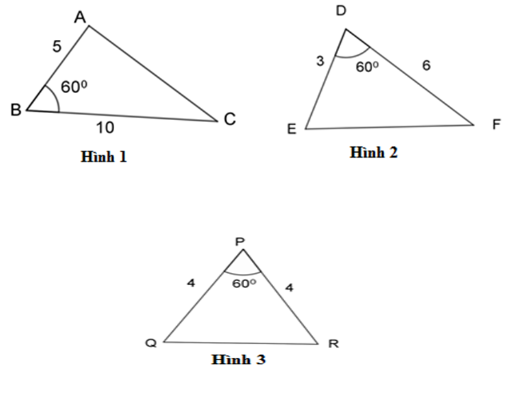
Hãy chỉ ra cặp tam giác đồng dạng với nhau từ các tam giác sau đây:
-
A.
Hình 1 và hình 2
-
B.
Hình 2 và hình 3
-
C.
Hình 1 và hình 3
-
D.
Tất cả đều đúng.
Cho \(\Delta ABC\), lấy 2 điểm $D$ và $E$ lần lượt nằm bên cạnh $AB$ và $AC$ sao cho \(\dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}}\). Kết luận nào sai?
-
A.
\(\Delta \;ADE\backsim\Delta \;ABC\)
-
B.
\(DE{\rm{//}}BC\)
-
C.
\(\dfrac{{AE}}{{AB}} = \dfrac{{AD}}{{AC}}\)
-
D.
\(\widehat {ADE} = \widehat {ABC}\)
Tính giá trị của $x$ trong hình dưới đây:
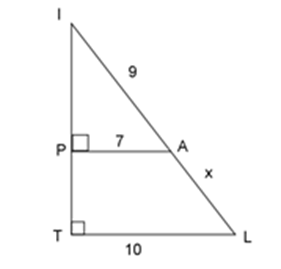
-
A.
$x = 3\,$
-
B.
$x = \dfrac{{27}}{7}$
-
C.
$x = 4\,$
-
D.
$x = \dfrac{{27}}{5}$
Tam giác ABC có $\widehat A = 2\widehat B$, $AB = 11\,{\rm{cm}}$, $AC = 25\,{\rm{cm}}$. Tính độ dài cạnh $BC$ .
-
A.
\(30\,cm\)
-
B.
\(20\,cm\)
-
C.
\(25\,cm\)
-
D.
\(15\,cm\)
Tam giác $ABC$ vuông tại $A$ có đường cao $AH$ . Cho biết $AB = 3cm$ ; $AC = 4cm$ . Tính độ dài các đoạn thẳng $HA, HB.$
-
A.
\(HA = 2,4\,cm;\,HB = 1,2\,cm\)
-
B.
\(HA = 2\,cm;\,HB = 1,8\,cm\)
-
C.
\(HA = 2\,cm;\,HB = 1,2\,cm\)
-
D.
\(HA = 2,4\,cm;\,HB = 1,8\,cm\)
Với giả thiết được cho trong hình, kết quả nào sau đây là đúng ?
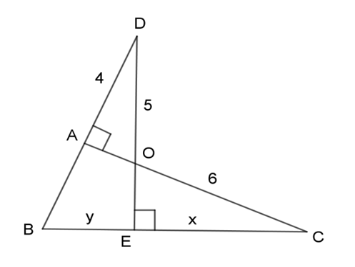
-
A.
\(y = 10\)
-
B.
\(x = 4,8\)
-
C.
\(x = 5\)
-
D.
\(y = 8,25\)
Hãy chọn câu đúng. Hình hộp chữ nhật có ba kích thước lần lượt là: $a$, $2a$, $\dfrac{a}{2}$ thể tích của hình hộp chữ nhật đó là:
-
A.
${a^2}$
-
B.
$4{a^2}$
-
C.
$2{a^4}$
-
D.
${a^3}$
Cho hình hộp chữ nhật $ABCD.A'B'C'D'$. Có bao nhiêu cạnh song song với cạnh $AB$
-
A.
$4$.
-
B.
$3$.
-
C.
$2$.
-
D.
$5$.
Cho hình lập phương $ABCD.A'B'C'D'$. Tính số đo góc \(AB'C\) .
-
A.
$90^\circ $.
-
B.
$45^\circ $.
-
C.
$30^\circ $.
-
D.
$60^\circ $.
Một hình hộp chữ nhật có diện tích xung quanh bằng $120\,c{m^2}$ , chiều cao bằng $6cm$ . Tìm các kích thước của đáy để hình hộp chữ nhật có thể tích lớn nhất.
-
A.
\(8\,cm\)
-
B.
\(7\,cm\)
-
C.
\(6\,cm\)
-
D.
\(5\,cm\)
Tính diện tích xung quanh của hình chóp cụt tứ giác đều có các cạnh đáy bằng $6cm$ và $8cm$ , chiều cao của mặt bên bằng $5cm$ .
-
A.
$120\,c{m^2}$
-
B.
$70\,c{m^2}$
-
C.
$150\,c{m^2}$
-
D.
$140\,c{m^2}$
Lời giải và đáp án
Chọn khẳng định đúng.
-
A.
3 là nghiệm của phương trình \({x^2} - 9 = 0\)
-
B.
\(\left\{ 3 \right\}\) là tập nghiệm của phương trình \({x^2} - 9 = 0\)
-
C.
Tập nghiệm của phương trình \((x + 3)(x - 3) = {x^2} - 9\) là \(\mathbb{Q}\)
-
D.
\(x = 2\) là nghiệm duy nhất của phương trình \({x^2} - 4 = 0\) .
Đáp án : A
Tìm tập nghiệm của mỗi phương trình rồi kết luận.
+ Ta có \({x^2} - 9 = 0 \Leftrightarrow {x^2} = 9 \Leftrightarrow x = \pm 3\) . Nên \(x = 3\) là nghiệm của phương trình \({x^2} - 9 = 0\) và tập nghiệm của phương trình là \(\left\{ {3; - 3} \right\}\). Suy ra A đúng, B sai.
+ Xét \((x + 3)(x - 3) = {x^2} - 9\)\( \Leftrightarrow {x^2} - 9 = {x^2} - 9\) (luôn đúng) nên tập nghiệm của phương trình là \(\mathbb{R}\), suy ra C sai.
+ Xét \({x^2} - 4 = 0 \Leftrightarrow {x^2} = 4 \Leftrightarrow x = \pm 2 \Rightarrow \) phương trình có hai nghiệm \(x = 2;\,x = - 2\) nên D sai.
Phương trình \(2x - 3 = 12 - 3x\) có bao nhiêu nghiệm?
-
A.
\(0\)
-
B.
\(1\)
-
C.
\(2\)
-
D.
Vô số nghiệm
Đáp án : B
Chuyển hạng tử chứa ẩn sang vế trái, hạng tử tự do về vế phải, thu gọn rồi chia hai vế cho hệ số của ẩn (nếu cần) ta tìm được nghiệm( chú ý khi chuyển vế hạng tử phải đổi dấu hạng tử đó).
Ta có
\(\begin{array}{l}2x - 3 = 12 - 3x\\ 2x + 3x = 12 + 3\\ 5x = 15\\ = 15:5\\ x = 3\end{array}\)
Vậy phương trình có một nghiệm duy nhất \(x = 3\) .
Tính tổng các nghiệm của phương trình \(\left| {3x + 6} \right| - 2 = 4\), biết phương trình có hai nghiệm phân biệt.
-
A.
$0$
-
B.
$10$
-
C.
$4$
-
D.
$ - 4$
Đáp án : D
+ Chuyển vế đưa phương trình về dạng \(\left| A \right| = B\)
+ Giải phương trình \(\left| A \right| = B \Leftrightarrow \left[ \begin{array}{l}A = B\\A = - B\end{array} \right.\)
Ta có:
\(\begin{array}{l}\left| {3x + 6} \right| - 3 = 3 \Leftrightarrow \left| {3x + 6} \right| = 6\\ \Leftrightarrow \left[ \begin{array}{l}3x + 6 = 6\\3x + 6 = - 6\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}3x = 0\\3x = - 12\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = - 4\end{array} \right.\end{array}\)
Vậy tổng các nghiệm của phương trình là \(0 + \left( { - 4} \right) = - 4\).
Chọn khẳng định đúng.
-
A.
Phương trình \(8x\left( {3x - 5} \right) = 6\left( {3x - 5} \right)\)có hai nghiệm trái dấu
-
B.
Phương trình \(8x\left( {3x - 5} \right) = 6\left( {3x - 5} \right)\)có hai nghiệm cùng dương
-
C.
Phương trình \(8x\left( {3x - 5} \right) = 6\left( {3x - 5} \right)\)có hai nghiệm cùng âm
-
D.
Phương trình \(8x\left( {3x - 5} \right) = 6\left( {3x - 5} \right)\)có một nghiệm duy nhất
Đáp án : B
Ta biến đổi phương trình đã cho về dạng \(A\left( x \right).B\left( x \right) = 0 \Leftrightarrow A\left( x \right) = 0\) hoặc \(B\left( x \right) = 0\)
Ta có \(8x\left( {3x - 5} \right) = 6\left( {3x - 5} \right)\)
\(8x\left( {3x - 5} \right) - 6\left( {3x - 5} \right) = 0\\ \left( {8x - 6} \right)\left( {3x - 5} \right) = 0\)
\(+)\,8x - 6 = 0\\8x = 6\\x = \dfrac{3}{4}\)
\(+)\,3x - 5 = 0\\3x = 5\\x = \dfrac{5}{3}\)
Vậy phương trình đã cho có hai nghiệm cùng dương \(x = \dfrac{3}{4};\,x = \dfrac{5}{3}\) .
Một số em thấy nhân tử \(\left( {3x - 5} \right)\) xuất hiện ở cả hai vế nên đã rút gọn, dẫn đến còn lại \(8x = 6\) . Do đó bị thiếu nghiệm \(x = \dfrac{5}{3}\) .
Biết rằng phương trình \({\left( {{x^2} - 1} \right)^2} = 4x + 1\) có nghiệm lớn nhất là \({x_0}\) . Chọn hẳng định đúng.
-
A.
\({x_0} = 3\)
-
B.
\({x_0} < 2\)
-
C.
\({x_0} > 1\)
-
D.
\({x_0} < 0\)
Đáp án : C
+ Thêm \(4{x^2}\) vào hai vế rồi đưa phương trình về dạng \({A^2} = {B^2} \) thì \(A = B\) hoặc \(A = - B\)
Cộng \(4{x^2}\) vào hai vế ta được
\({\left( {{x^2} - 1} \right)^2} = 4x + 1 {x^4} - 2{x^2} + 1 = 4x + 1\\ {x^4} - 2{x^2} + 1 + 4{x^2} = 4{x^2} + 4x + 1\\ {x^4} + 2{x^2} + 1 = 4{x^2} + 4x + 1\\ {\left( {{x^2} + 1} \right)^2} = {\left( {2x + 1} \right)^2}\)
\(+)\,{x^2} + 1 = 2x + 1\\{x^2} - 2x = 0\\x\left( {x - 2} \right) = 0\)
Suy ra \(x = 0\) hoặc \(x = 2\)
\(+)\,{x^2} + 1 = - 2x – 1\\{x^2} + 2x + 2 = 0\\{\left( {x + 1} \right)^2} + 1 = 0\,\left( {VN} \right)\)
Vậy \(S = \left\{ {0;2} \right\}\) , nghiệm lớn nhất là \({x_0} = 2 > 1\) .
Hãy chọn câu đúng. Điều kiện xác định của phương trình \(\dfrac{1}{{x - 2}} + 3 = \dfrac{{3 - x}}{{x - 2}}\) là
-
A.
\(x \ne 3\)
-
B.
\(x \ne 2\)
-
C.
\(x \ne - 3\)
-
D.
\(x \ne - 2\)
Đáp án : B
Tìm các điều kiện để tất cả các mẫu thức trong phương trình khác $0$.
ĐK: \(x - 2 \ne 0 \) hay \(x \ne 2\).
Cho hai biểu thức : \(A = 1 + \dfrac{1}{{2 + x}}\) và \(B = \dfrac{{12}}{{{x^3} + 8}}\) . Tìm $x$ sao cho \(A = B\) .
-
A.
\(x = 0\)
-
B.
\(x = 1\)
-
C.
\(x = - 1\)
-
D.
Cả A và B.
Đáp án : D
Cho \(A = B\) rồi giải phương trình chứa ẩn ở mẫu theo các bước:
+ Tìm ĐKXĐ của phương trình.
+ Quy đồng mẫu rồi khử mẫu.
+ Giải phương trình vừa nhận được .
+ Đối chiếu điều kiện rồi kết luận nghiệm.
Để \(A = B\) thì \(1 + \dfrac{1}{{2 + x}} = \dfrac{{12}}{{{x^3} + 8}}\) .
ĐKXĐ: \(x \ne - 2\)
\(1 + \dfrac{1}{{2 + x}} = \dfrac{{12}}{{{x^3} + 8}}\,\,\\1 + \dfrac{1}{{x + 2}} = \dfrac{{12}}{{\left( {x + 2} \right)\left( {{x^2} - 2x + 4} \right)}}\\\dfrac{{{x^3} + 8 + {x^2} - 2x + 4}}{{\left( {x + 2} \right)\left( {{x^2} - 2x + 4} \right)}} = \dfrac{{12}}{{\left( {x + 2} \right)\left( {{x^2} - 2x + 4} \right)}}\\{x^3} + 8 + {x^2} - 2x + 4 = 12\\{x^3} + {x^2} - 2x = 0 \\x\left( {{x^2} + x - 2} \right) = 0\\x\left( {{x^2} - x + 2x - 2} \right) = 0 \\x\left( {x - 1} \right)\left( {x + 2} \right) = 0\)
Suy ra \(x = 0\) hoặc \(x - 1 = 0\) hoặc \(x + 2 = 0\)
hay \(x = 0\,\,\,\,(tm)\) hoặc \(x = 1\,\,\,\,(tm)\) hoặc \(x = - 2\,\,\,\,(ktm)\)
Vậy để \(A = B\) thì \(x = 0\) hoặc \(x = 1\).
Hai xe khởi hành cùng một lúc, xe thứ nhất đến sớm hơn xe thứ hai $3$ giờ. Nếu gọi thời gian đi của xe thứ nhất là $x$ giờ thì thời gian đi của xe thứ hai là:
-
A.
\((x - 3)\) giờ
-
B.
\(3x\) giờ
-
C.
\((3 - x)\) giờ
-
D.
\((x + 3)\) giờ
Đáp án : D
Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết.
Vì hai xe khởi hành cùng một lúc, xe thứ nhất đến sớm hơn xe thứ hai $3$ giờ nên thời gian xe thứ hai đi nhiều hơn xe thứ nhất \(3\) giờ.
Nếu thời gian đi của xe thứ nhất là $x$ giờ thì thời gian đi của xe thứ hai là \(x + 3\) giờ.
Một đội máy cày dự định cày $40$ ha ruộng $1$ ngày. Do sự cố gắng, đội đã cày được $52$ ha mỗi ngày. Vì vậy, chẳng những đội đã hoàn thành sớm hơn $2$ ngày mà còn cày vượt mức được $4$ ha nữa. Tính diện tích ruộng đội phải cày theo dự định.
-
A.
\(300\) ha
-
B.
\(630\) ha
-
C.
\(420\) ha
-
D.
\(360\) ha
Đáp án : D
Giải theo các bước sau:
+ Lập phương trình: Chọn ẩn và đặt điều kiện; biểu diễn đại lượng chưa biết theo ẩn và đại lượng đã biết; lập Phương trình biểu thị mối quan hệ giữa các đại lượng
+ Giải phương trình
+ Đối chiếu điều kiện rồi kết luận
Gọi số ngày dự kiến đội hoàn thành cày ruộng theo kế hoạch là \(x\) (ngày, $x > 0$ ).
Đội hoàn thành diện tích ruộng theo kế hoạch là: \(40x\) (ha).
Thời gian thực tế đội hoàn thành diện tích ruộng là: \(x - 2\) (ngày).
Đội hoàn thành diện tích ruộng theo thực tế là: \(52(x - 2)\) (ha).
Vì tổ vượt mức \(4\) ha nên ta có phương trình:
\(52\left( {x - 2} \right) = 40x + 4 \Leftrightarrow 12x = 108\) \( \Leftrightarrow x = 9\) (thỏa mãn)
Vậy diện tích ruộng cần cày theo dự định là \(9.40 = 360\,\) ha.
Trong tháng Giêng hai tổ công nhân may được $800$ chiếc áo. Tháng Hai, tổ $1$ vượt mức $15\% $ , tổ hai vượt mức $20\% $ do đó cả hai tổ sản xuất được $945$ cái áo. Tính xem trong tháng đầu, tổ \(1\) may được bao nhiêu chiếc áo?
-
A.
\(300\)
-
B.
\(500\)
-
C.
\(400\)
-
D.
\(600\)
Đáp án : A
Giải theo các bước sau:
+ Lập phương trình: Chọn ẩn và đặt điều kiện; biểu diễn đại lượng chưa biết theo ẩn và đại lượng đã biết; lập Phương trình biểu thị mối quan hệ giữa các đại lượng
+ Giải phương trình
+ Đối chiếu điều kiện rồi kết luận
Gọi số áo tổ \(1\) làm được trong tháng Giêng là \(x\,\left( {x \in \mathbb{N}*;\,x < 800} \right)\)(áo)
Thì số áo tổ \(2\) làm được trong tháng Giêng là \(800 - x\) (áo)
Vì tháng hai, tổ \(1\) vượt mức $15\% $ nên số áo vượt mức là \(15\% .x = \dfrac{3}{{20}}x\) (áo)
Và tổ \(2\) vượt mức \(20\% \) nên số áo vượt mức là \(20\% \left( {800 - x} \right) = \dfrac{{800 - x}}{5}\) (áo)
Vì tháng hai, cả hai tổ sản xuất được $945$ cái áo nên vượt mức với tháng Giêng là \(945 - 800 = 145\) áo
Nên ta có phương trình \(\dfrac{3}{{20}}x + \dfrac{{800 - x}}{5} = 145 \Leftrightarrow 3x + 3200 - 4x = 2900 \Leftrightarrow x = 300\,\left( {TM} \right)\) .
Vậy trong tháng Giêng tổ một làm được \(300\) áo.
So sánh $m$ và $n$ biết $m-\dfrac{1}{2} = n$
-
A.
\(m < n\)
-
B.
\(m = n\)
-
C.
\(m \le n\)
-
D.
\(m > n\)
Đáp án : D
+ Chuyển vế đổi dấu
+ So sánh với $0$
+ So sánh $m$ và $n$
Ta có: \(m - \dfrac{1}{2} = n \)
\(m - n = \dfrac{1}{2} \)
\(m - n > 0 \)
\(m > n\) .
Với \(a,b\) bất kỳ. Chọn khẳng định sai.
-
A.
\({a^2} + 5 > 4a\)
-
B.
\({a^2} + 10 < 6a - 1\)
-
C.
\({a^2} + 1 > a\)
-
D.
\(ab - {b^2} \le {a^2}\)
Đáp án : B
Phương pháp xét hiệu.
* ${a^2} + 5 - 4a = {a^2} - 4a + 4 + 1 = {(a - 2)^2} + 1 > 0$ (luôn đúng) nên \({a^2} + 5 > 4a\)
* ${a^2} + 1 - a = {a^2} - 2a.\dfrac{1}{2} + \dfrac{1}{4} + \dfrac{3}{4} = {\left( {a - \dfrac{1}{2}} \right)^2} + \dfrac{3}{4} > 0$ (luôn đúng) nên \({a^2} + 1 > a\)
\(\begin{array}{l}{a^2} + 10 - \left( {6a + 1} \right)\\ = {a^2} - 6a + 10 - 1\\ = {a^2} - 6a + 9\\ = {\left( {a - 3} \right)^2} \ge 0\end{array}\)
Vì \({(a - 3)^2} \ge 0\) (luôn đúng) nên \({a^2} + 10 > 6a + 1\) . Do đó B sai.
* Ta có:
\(\begin{array}{l}{a^2} \ge ab - {b^2} \\ {a^2} - ab + {b^2} \ge 0\\ {a^2} - 2a.\dfrac{b}{2} + \dfrac{{{b^2}}}{4} + \dfrac{{3{b^2}}}{4} \ge 0 \\ {\left( {a - \dfrac{b}{2}} \right)^2} + \dfrac{{3{b^2}}}{4} \ge 0\end{array}\)
Vì \({\left( {a - \dfrac{b}{2}} \right)^2} + \dfrac{{3{b^2}}}{4} \ge 0\) (luôn đúng) nên \({a^2} \ge ab - {b^2}\).
Cho \(x + y > 1.\) Chọn khẳng định đúng
-
A.
\({x^2} + {y^2} > \dfrac{1}{2}\)
-
B.
\({x^2} + {y^2} < \dfrac{1}{2}\)
-
C.
\({x^2} + {y^2} = \dfrac{1}{2}\)
-
D.
\({x^2} + {y^2} \le \dfrac{1}{2}\)
Đáp án : A
+ Sử dụng các hằng đẳng thức cơ bản
+ Áp dụng tính chất liên hệ giữa thứ tự và phép cộng.
+ Áp dụng tính chất liên hệ giữa thứ tự và phép nhân.
Từ $x + y > 1$ , bình phương hai vế (hai vế đều dương) được ${x^2} + 2xy + {y^2} > 1$ (1)
Từ ${(x - y)^2} \ge 0$ suy ra ${x^2} - 2xy + {y^2} \ge 0.$(2)
Cộng từng vế (1) với (2) được $2{x^2} + 2{y^2} > 1.$
Chia hai vế cho $2$ được ${x^2} + {y^2} > \dfrac{1}{2}.$
Biểu diễn tập nghiệm của bất phương trình \(x \ge 8\) trên trục số, ta được
-
A.

-
B.

-
C.

-
D.
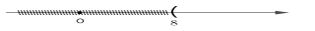
Đáp án : C
Biểu diễn tập nghiệm trên trục số

Ta biểu diễn \(x \ge 8\) trên trục số như sau:
Số nguyên lớn nhất thỏa mãn bất phương trình \(\dfrac{{1987 - x}}{{15}} + \dfrac{{1988 - x}}{{16}} + \dfrac{{27 + x}}{{1999}} + \dfrac{{28 + x}}{{2000}} > 4\) là
-
A.
$x > 1972$
-
B.
$x < 1972$
-
C.
$x < 1973$
-
D.
$x < 1297$
Đáp án : B
+ Cộng hai vế với \(\left( { - 4} \right)\), sau đó trừ mỗi phân thức cho \(1\)
+ Quy đồng hợp lý để xuất hiện nhân tử chung.
+ Đặt nhân tử chung và đánh giá hạng tử để giải bất phương trình
Ta có
\(\dfrac{{1987 - x}}{{15}} + \dfrac{{1988 - x}}{{16}} + \dfrac{{27 + x}}{{1999}} + \dfrac{{28 + x}}{{2000}} > 4\)
\( \dfrac{{1987 - x}}{{15}} + \dfrac{{1988 - x}}{{16}} + \dfrac{{27 + x}}{{1999}} + \dfrac{{28 + x}}{{2000}} - 4 > 0\)
\( \left( {\dfrac{{1987 - x}}{{15}} - 1} \right) + \left( {\dfrac{{1988 - x}}{{16}} - 1} \right) + \left( {\dfrac{{27 + x}}{{1999}} - 1} \right) + \left( {\dfrac{{28 + x}}{{2000}} - 1} \right) > 0\)
\( \dfrac{{1972 - x}}{{15}} + \dfrac{{1972 - x}}{{16}} + \dfrac{{x - 1972}}{{1999}} + \dfrac{{x - 1972}}{{2000}} > 0\)
\( \left( {1972 - x} \right)\left( {\dfrac{1}{{15}} + \dfrac{1}{{16}} - \dfrac{1}{{1999}} - \dfrac{1}{{2000}}} \right) > 0\)
Mà \(\dfrac{1}{{15}} + \dfrac{1}{{16}} - \dfrac{1}{{1999}} - \dfrac{1}{{2000}} > 0\) nên \(1972 - x > 0 \)\( x < 1972\)
Vậy \(x < 1972\) .
Nghiệm nhỏ nhất của phương trình \(\left| {2 + 3x} \right| = \left| {4x - 3} \right|\) là
-
A.
\(\dfrac{1}{7}\)
-
B.
\(5\)
-
C.
\( - \dfrac{1}{7}\)
-
D.
\( - 5\)
Đáp án : A
Vận dụng tính chất: \(\left| a \right| = \left| b \right| \Leftrightarrow \left[ \begin{array}{l}a = b\\a = - b\end{array} \right..\)
Ta có: \(\left| {A\left( x \right)} \right| = \left| {B\left( x \right)} \right| \Leftrightarrow \left[ \begin{array}{l}A\left( x \right) = B\left( x \right)\\A\left( x \right) = - B\left( x \right)\end{array} \right..\)
Ta có \(\left| {2 + 3x} \right| = \left| {4x - 3} \right|\)\( \Leftrightarrow \left[ \begin{array}{l}2 + 3x = 4x - 3\\2 + 3x = 3 - 4x\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 5\\7x = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 5\\x = \dfrac{1}{7}\end{array} \right.\)
Vậy nghiệm nhỏ nhất của phương trình là \(x = \dfrac{1}{7}\) .
Cho hai phương trình \(4\left| {2x - 1} \right| + 3 = 15\,\,\,\left( 1 \right)\) và \(\left| {7x + 1} \right| - \left| {5x + 6} \right| = 0\,\left( 2 \right)\). Kết luận nào sau đây là đúng.
-
A.
Phương trình \(\left( 1 \right)\) có nhiều nghiệm hơn phương trình \(\left( 2 \right)\)
-
B.
Phương trình \(\left( 1 \right)\) có ít nghiệm hơn phương trình \(\left( 2 \right)\)
-
C.
Cả hai phương trình đều có hai nghiệm phân biệt
-
D.
Cả hai phương trình đều vô số nghiệm
Đáp án : C
Để giải phương trình \(\left( 1 \right)\) ta thực hiện các bước sau:
+ Phá dấu giá trị tuyệt đối theo định nghĩa \(\left| a \right| = \left\{ \begin{array}{l}a\;\;khi\;\;a \ge 0\\ - a\;\;khi\;\;a < 0\end{array} \right..\)
+ Giải các phương trình bậc nhất một ẩn
+ So sánh với điều kiện và kết luận.
Để giải phương trình \(\left( 2 \right)\), ta chuyển vế biến đổi phương trình về dạng \(\left| {A\left( x \right)} \right| = \left| {B\left( x \right)} \right| \Leftrightarrow \left[ \begin{array}{l}A\left( x \right) = B\left( x \right)\\A\left( x \right) = - B\left( x \right)\end{array} \right.\)
* Xét phương trình \(4\left| {2x - 1} \right| + 3 = 15\,\,\,\left( 1 \right)\)
TH1: \(\left| {2x - 1} \right| = 2x - 1\) khi \(x \ge \dfrac{1}{2}\)
Phương trình \(\left( 1 \right)\) trở thành \(4\left( {2x - 1} \right) + 3 = 15 \)\(\Leftrightarrow 4\left( {2x - 1} \right) = 12 \)\(\Leftrightarrow 2x - 1 = 3 \)\(\Leftrightarrow x = 2\,\left( {TM} \right)\)
TH2: \(\left| {2x - 1} \right| = 1 - 2x\) khi \(x < \dfrac{1}{2}\)
Phương trình \(\left( 1 \right)\) trở thành \(4\left( {1 - 2x} \right) + 3 = 15 \)\(\Leftrightarrow 4\left( {1 - 2x} \right) = 12 \)\(\Leftrightarrow 1 - 2x = 3 \)\( \Leftrightarrow x = - 1\left( {TM} \right)\)
Vậy phương trình \(\left( 1 \right)\) có hai nghiệm \(x = - 1;\,x = 2\).
Xét phương trình
\(\;\left| {7x + 1} \right| - \left| {5x + 6} \right| = 0\\ \Leftrightarrow \left| {7x + 1} \right| = \left| {5x + 6} \right|\\ \Leftrightarrow \left[ \begin{array}{l}7x + 1 = 5x + 6\\7x + 1 = - (5x + 6)\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}2x = 5\\12x = - 7\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{5}{2}\\x = - \dfrac{7}{{12}}\end{array} \right.\)
Vậy phương trình \(\left( 2 \right)\) có hai nghiệm là \(x = \dfrac{5}{2};x = - \dfrac{7}{{12}}.\)
Hãy chọn câu đúng. Tỉ số \(\dfrac{x}{y}\) của các đoạn thẳng trong hình vẽ, biết rằng các số trên hình cùng đơn vị đo là $cm$ .

-
A.
\(\dfrac{7}{{15}}\)
-
B.
\(\dfrac{1}{7}\)
-
C.
\(\dfrac{{15}}{7}\)
-
D.
\(\dfrac{1}{{15}}\)
Đáp án : A
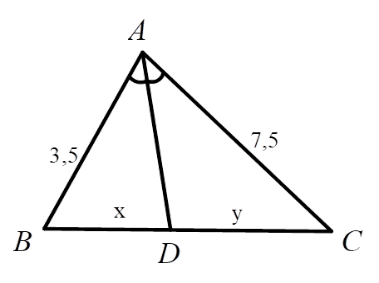
Xét tam giác \(ABC\), vì \(AD\) là phân giác góc \(\widehat {BAC}\) nên ta có:
\(\dfrac{{BD}}{{DC}} = \dfrac{{AB}}{{AC}}\)
\(\dfrac{x}{y} = \dfrac{{3,5}}{{7,5}} = \dfrac{7}{{15}}\)
Cho \(\Delta ABC\), \(AE\) là phân giác ngoài của góc A. Hãy chọn câu đúng:

-
A.
\(\dfrac{{AB}}{{AE}} = \dfrac{{BE}}{{CE}}\).
-
B.
\(\dfrac{{AE}}{{AC}} = \dfrac{{BE}}{{CE}}\).
-
C.
\(\dfrac{{AB}}{{AC}} = \dfrac{{CE}}{{BE}}\).
-
D.
\(\dfrac{{AB}}{{AC}} = \dfrac{{BE}}{{CE}}\).
Đáp án : D
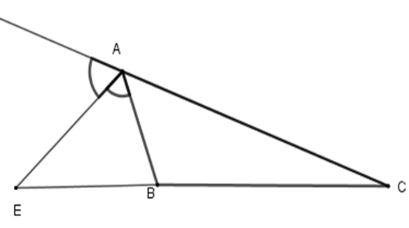
Vì trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hoai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy nên \(\dfrac{{AB}}{{AC}} = \dfrac{{BE}}{{CE}}\)
Nếu tam giác $ABC$ có $MN$ // $BC$ (với \(M\in AB, N\in AC)\) thì
-
A.
\({\rm{\Delta }}AMN\) đồng dạng với \({\rm{\Delta }}ACB\).
-
B.
\({\rm{\Delta }}ABC\) đồng dạng với \({\rm{\Delta }}MNA\).
-
C.
\({\rm{\Delta }}AMN\) đồng dạng với \({\rm{\Delta }}ABC\).
-
D.
\({\rm{\Delta }}ABC\) đồng dạng với \({\rm{\Delta }}ANM\).
Đáp án : C
Sử dụng định lý: Nếu một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
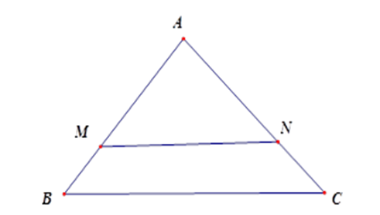
Vì \(MN{\rm{//}}BC \Rightarrow \) tam giác \(AMN\) đồng dạng với tam giác \(\Delta ABC\) .
Khi viết hai tam giác đồng dạng ta phải viết đúng thứ tự các góc tương ứng bằng nhau và các cạnh tương ứng tỉ lệ.
Một tam giác có cạnh nhỏ nhất bằng $8$ , hai cạnh còn lại bằng $x$ và $y$ \(\left( {x < y} \right).\) Một tam giác khác có cạnh lớn nhất bằng $27$ , hai cạnh còn lại cũng bằng $x$ và $y$ . Tính $x$ và $y$ để hai tam giác đó đồng dạng.
-
A.
$x = 5;\,y = 10$.
-
B.
$x = 6;\,y = 12$
-
C.
$x = 12;\,y = 18$
-
D.
$x = 6;\,y = 18$
Đáp án : C
+ Sắp xếp các cạnh của tam giác theo thứ tự tăng dần.
+ Lập tỉ lệ cạnh và tính $x,y$ .
Tam giác thứ nhất có các cạnh là \(8 < x < y\)
Tam giác thứ hai có các cạnh là $x < y < 27$ .
Vì hai tam giác đồng dạng nên \(\dfrac{8}{x} = \dfrac{x}{y} = \dfrac{y}{{27}}\) ta có \(x.y = 8.27\) và \({x^2} = 8y.\)
Do đó \({x^2} = 8y = 8 \cdot \dfrac{{8.27}}{x}\)nên \({x^3} = 64.27 = {\left( {4.3} \right)^3}.\)
Vậy \(x = 12,y = 18.\)
Hãy chỉ ra cặp tam giác đồng dạng với nhau từ các tam giác sau đây:

-
A.
Hình 1 và hình 2
-
B.
Hình 2 và hình 3
-
C.
Hình 1 và hình 3
-
D.
Tất cả đều đúng.
Đáp án : A
Bước 1: Xét tỉ số độ dài của các cặp cạnh từng tam giác.
Bước 2: Thấy cặp tam giác nào có tỉ số cặp cạnh của từng tam giác bằng nhau và góc xen giữa cặp cạnh đó bằng nhau thì cặp cạnh đang xét đồng dạng với nhau theo trường hợp cạnh – góc – cạnh.
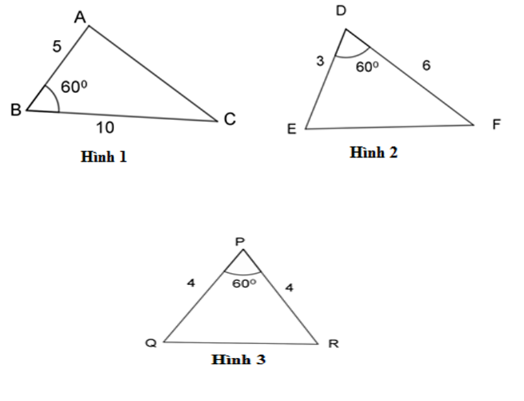
Có: \(\dfrac{{BA}}{{BC}} = \dfrac{5}{{10}} = \dfrac{1}{2},\;\dfrac{{DE}}{{DF}} = \dfrac{3}{6} = \dfrac{1}{2},\;\dfrac{{PQ}}{{PR}} = \dfrac{4}{4} = 1 \Rightarrow \dfrac{{BA}}{{BC}} = \dfrac{{DE}}{{DF}} = \dfrac{1}{2}.\)
Xét \(\Delta ABC\) và $\Delta EDF$ ta có:
$\dfrac{{BA}}{{BC}} = \dfrac{{DE}}{{DF}}\,\,\left( {cmt} \right) $$\Leftrightarrow \dfrac{{DE}}{{BA}} = \dfrac{{DF}}{{BC}}$
$\widehat B = \widehat D = {60^0}\;(gt)$
$\Rightarrow \Delta ABC\backsim \Delta EDF\,\,\,\left( {c - g - c} \right).$
- Học sinh cần xác định đúng chứng minh cặp tam giác đồng dạng theo trường hợp nào để tìm ra kết quả tối ưu nhất.
- Học sinh cần viết các cặp đoạn thẳng tỉ lệ và cặp tam giác đồng dạng theo đúng thứ tự đỉnh tương ứng của 2 tam giác.
Cho \(\Delta ABC\), lấy 2 điểm $D$ và $E$ lần lượt nằm bên cạnh $AB$ và $AC$ sao cho \(\dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}}\). Kết luận nào sai?
-
A.
\(\Delta \;ADE\backsim\Delta \;ABC\)
-
B.
\(DE{\rm{//}}BC\)
-
C.
\(\dfrac{{AE}}{{AB}} = \dfrac{{AD}}{{AC}}\)
-
D.
\(\widehat {ADE} = \widehat {ABC}\)
Đáp án : C
Bước 1: Chứng minh cặp tam giác đồng dạng theo trường hợp cạnh – góc – cạnh.
Bước 2: Áp dụng định lý Talet đảo để tìm ra nhận định sai.
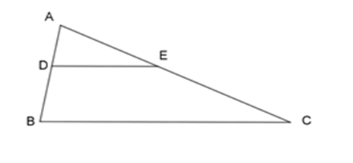
Xét $\Delta ADE$ và $\Delta ABC$ ta có:
\(\dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}}\) (theo gt)
$\widehat A$ chung.
$ \Rightarrow \Delta ADE\backsim\Delta ABC$ (c – g – c)
$ \Rightarrow \widehat {ADE} = \widehat {ABC}$ (cặp góc tương ứng)
$ \Rightarrow \dfrac{{AD}}{{AB}} = \dfrac{{AE}}{{AC}} = \dfrac{{DE}}{{BC}} \Rightarrow DE{\rm{//}}BC$ (định lý Talet đảo)
- Học sinh cần viết các cặp đoạn thẳng tỉ lệ và cặp tam giác đồng dạng theo đúng thứ tự đỉnh tương ứng của 2 tam giác.
Tính giá trị của $x$ trong hình dưới đây:

-
A.
$x = 3\,$
-
B.
$x = \dfrac{{27}}{7}$
-
C.
$x = 4\,$
-
D.
$x = \dfrac{{27}}{5}$
Đáp án : B
Bước 1: Chứng minh 2 tam giác đồng dạng theo trường hợp góc – góc.
Bước 2: Từ đó ta rút ra được tỉ lệ thức phù hợp, tính ra giá trị $x$ .
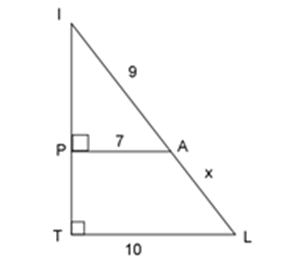
Xét \(\Delta IPA\) và \(\Delta ITL\) ta có:
\(+) \widehat {IPA} = \widehat {ITL} = {90^0}\\ +) \widehat {TIL}\,\,\,chung\\ \Rightarrow \Delta IPA\backsim\Delta ITL\;(g - g)\\ \Rightarrow \dfrac{{PA}}{{TL}} = \dfrac{{IA}}{{IL}} \Leftrightarrow \dfrac{{PA}}{{TL}} = \dfrac{{IA}}{{IA + AL}} \Leftrightarrow \dfrac{7}{{10}} = \dfrac{9}{{9 + x}}\)\( \Leftrightarrow x = \dfrac{{27}}{7}\)
- Học sinh cần viết các cặp tam giác đồng dạng theo đúng thứ tự đỉnh tương ứng của $2$ tam giác.
- Học sinh cần tránh mắc sai lầm trong tính toán.
Tam giác ABC có $\widehat A = 2\widehat B$, $AB = 11\,{\rm{cm}}$, $AC = 25\,{\rm{cm}}$. Tính độ dài cạnh $BC$ .
-
A.
\(30\,cm\)
-
B.
\(20\,cm\)
-
C.
\(25\,cm\)
-
D.
\(15\,cm\)
Đáp án : A
Bước 1: Trên tia đối của tia $AC$ lấy điểm $D$ sao cho $AD = AB$
Bước 2: Tìm dữ kiện cần để chứng minh cặp tam giác đồng dạng theo trường hợp góc – góc.
Bước 3: Từ tam giác đồng dạng suy ra tỉ lệ cạnh thích hợp để tính \(BC\) .
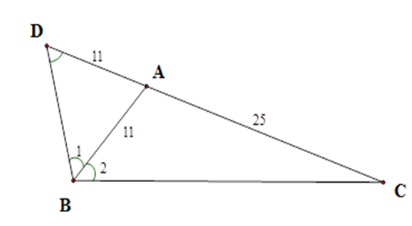
Trên tia đối của tia $AC$ lấy điểm $D$ sao cho $AD = AB$ .
Tam giác $ABD$ cân tại $A$ nên \(\widehat {BAC} = \widehat {{B_1}} + \widehat D = 2\widehat D\) .
Ta lại có $\widehat {BAC} = 2\widehat {{B_2}}$ nên \(\widehat D = \widehat {{B_2}}\) .
Xét \(\Delta CBA\) và \(\Delta CDB\) có \(\widehat C\) chung và \(\widehat D = \widehat {{B_2}}\)
Nên \(\Delta CBA\backsim\Delta CDB\,\left( {g - g} \right)\) nên \(\dfrac{{CB}}{{CD}} = \dfrac{{AC}}{{BC}}\) ,
tức là \(\dfrac{{CB}}{{36}} = \dfrac{{25}}{{BC}}\). Từ đó \(B{C^2} = 25.36\)
suy ra \(BC = 5.6 = 30(cm)\).
Tam giác $ABC$ vuông tại $A$ có đường cao $AH$ . Cho biết $AB = 3cm$ ; $AC = 4cm$ . Tính độ dài các đoạn thẳng $HA, HB.$
-
A.
\(HA = 2,4\,cm;\,HB = 1,2\,cm\)
-
B.
\(HA = 2\,cm;\,HB = 1,8\,cm\)
-
C.
\(HA = 2\,cm;\,HB = 1,2\,cm\)
-
D.
\(HA = 2,4\,cm;\,HB = 1,8\,cm\)
Đáp án : D
- Chứng minh các cặp tam giác đồng dạng phù hợp để tìm ra tỉ lệ thức thích hợp.
- Tính độ dài các cạnh cần tìm dựa vào định lý Pitago và dữ kiện đã có.
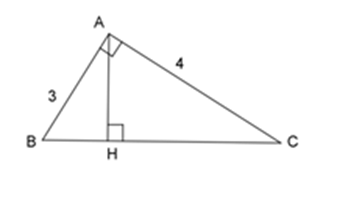
Áp dụng định lý Pytago vào tam giác vuông $ABC$ ta có:
\(\begin{array}{l}A{B^2} + A{C^2} = B{C^2}\\ \Leftrightarrow {3^2} + {4^2} = B{C^2}\\ \Leftrightarrow B{C^2} = 25\\ \Rightarrow BC = 5\;cm\end{array}\)
Xét 2 tam giác vuông $ABC$ và $HBA$ có: \(\widehat B\) chung
\( \Rightarrow \Delta ABC\backsim\Delta HBA\;(g - g)\)
\( \Rightarrow \dfrac{{AB}}{{HB}} = \dfrac{{BC}}{{BA}} \Rightarrow HB = \dfrac{{A{B^2}}}{{BC}} = \dfrac{{{3^2}}}{5} = 1,8\;cm\)
Mặt khác:
\(\dfrac{{AB}}{{HB}} = \dfrac{{AC}}{{HA}} \Rightarrow HA = \dfrac{{AC.HB}}{{AB}} = \dfrac{{4.1,8}}{3} = 2,4\;cm\)
Nên \(HA = 2,4\,cm;\,HB = 1,8\,cm\) .
- Học sinh cần viết tỉ lệ đồng dạng theo đúng thứ tự đỉnh, cạnh tương ứng của 2 tam giác.
- Học sinh cần chú ý trong kĩ năng đại số tránh mắc sai lầm trong tính toán.
Với giả thiết được cho trong hình, kết quả nào sau đây là đúng ?

-
A.
\(y = 10\)
-
B.
\(x = 4,8\)
-
C.
\(x = 5\)
-
D.
\(y = 8,25\)
Đáp án : B
- Chứng minh các cặp tam giác đồng dạng phù hợp để tìm ra tỉ lệ thức thích hợp.
- Tính độ dài $x,y$ dựa vào dữ kiện tìm được và dữ kiện đề bài đã cho (áp dụng định lý Pytago).
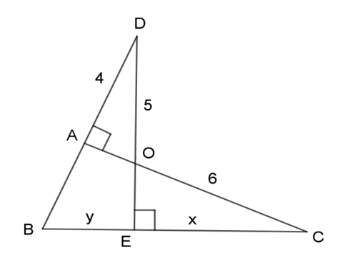
Xét 2 tam giác vuông \(\Delta ADO\)\((\widehat {DAO} = {90^0})\) và \(\Delta ECO\)\((\widehat {CEO} = {90^0})\) ta có:
\(\widehat {AOD} = \widehat {EOC}\) (2 góc đối đỉnh)
\( \Rightarrow \Delta ADO\backsim\Delta ECO\;(g - g)\)
\( \Rightarrow \dfrac{{AD}}{{EC}} = \dfrac{{DO}}{{CO}} \Leftrightarrow \dfrac{4}{x} = \dfrac{5}{6} \Leftrightarrow x = \dfrac{{4.6}}{5} = 4,8\)
Vì \(\Delta ADO\) vuông tại A nên áp dụng định lý Pitago ta có:
\(\begin{array}{l}\,\,\,\,\,\,\,\,A{D^2} + A{O^2} = O{D^2}\\ \Leftrightarrow {4^2} + A{O^2} = {5^2}\\ \Leftrightarrow A{O^2} = {5^2} - {4^2} = 9\\ \Rightarrow AO = 3\end{array}\)
Xét 2 tam giác vuông \(\Delta CEO\;(\widehat {CEO} = {90^0})\) và \(\Delta CAB\;(\widehat {CAB} = {90^0})\) có:\(\widehat C\) chung
\( \Rightarrow \dfrac{{CO}}{{CB}} = \dfrac{{CE}}{{CA}} \Leftrightarrow \dfrac{{CO}}{{CE + EB}} = \dfrac{{CE}}{{CO + OA}} \Leftrightarrow \dfrac{6}{{4,8 + y}} = \dfrac{{4,8}}{{6 + 3}} \Leftrightarrow y = 6,45\)
Vậy \(x = 4,8;\;y = 6,45\).
- Học sinh cần viết tỉ lệ đồng dạng theo đúng thứ tự đỉnh, cạnh tương ứng của 2 tam giác.
- Học sinh cần chú ý trong kĩ năng đại số tránh mắc sai lầm trong tính toán.
Hãy chọn câu đúng. Hình hộp chữ nhật có ba kích thước lần lượt là: $a$, $2a$, $\dfrac{a}{2}$ thể tích của hình hộp chữ nhật đó là:
-
A.
${a^2}$
-
B.
$4{a^2}$
-
C.
$2{a^4}$
-
D.
${a^3}$
Đáp án : D
Sử dụng công thức thể tích của hình hộp chữ nhật $V = abc$ ($a,b,c$ là các kích thước của hình hộp chữ nhật)
Thể tích của hình hộp chữ nhật là \(V = a.2a.\dfrac{a}{2} = {a^3}\) (đvtt)
Các em cần nhớ đúng công thức khi tính toán.
Cho hình hộp chữ nhật $ABCD.A'B'C'D'$. Có bao nhiêu cạnh song song với cạnh $AB$
-
A.
$4$.
-
B.
$3$.
-
C.
$2$.
-
D.
$5$.
Đáp án : B
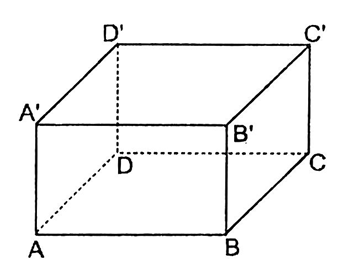
Có ba cạnh song song với $AB$ là $A'B',CD,C'D'$ .
Cho hình lập phương $ABCD.A'B'C'D'$. Tính số đo góc \(AB'C\) .
-
A.
$90^\circ $.
-
B.
$45^\circ $.
-
C.
$30^\circ $.
-
D.
$60^\circ $.
Đáp án : D
Mối quan hệ giữa các cạnh trong hình hộp chữ nhật từ đó suy ra số đo góc.
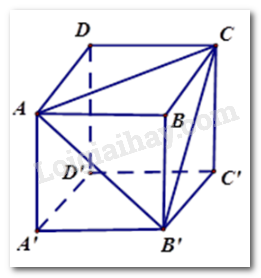
Các tam giác $ABC,ABB',CBB'$ vuông cân nên $AC = AB' = B'C$ .
Tam giác $AB'C$ có ba cạnh bằng nhau nên là tam giác đều, suy ra \(\widehat {AB'C} = {60^0}\) .
Một hình hộp chữ nhật có diện tích xung quanh bằng $120\,c{m^2}$ , chiều cao bằng $6cm$ . Tìm các kích thước của đáy để hình hộp chữ nhật có thể tích lớn nhất.
-
A.
\(8\,cm\)
-
B.
\(7\,cm\)
-
C.
\(6\,cm\)
-
D.
\(5\,cm\)
Đáp án : D
+ Sử dụng công thức thể tích và diện tích xung quanh của hình hộp chữ nhật.
+ Dùng hằng đẳng thức để biện luận theo yêu cầu đề bài.
Gọi $a$ và $b$ là các kích thước của đáy.
Ta có $V = 6ab$ nên $V$ lớn nhất \( \Leftrightarrow \) $ab$ lớn nhất
\({S_{xq}} = 120\) nên \(2\left( {a + b} \right).6 = 120\) hay \(a + b = 10\).
Ta có: \(ab = a\left( {10 - a} \right) = - {a^2} + 10a = - {\left( {a - 5} \right)^2} + 25 \le 25\).
Suy ra \(V = 6ab \le 6.25 = 150\).
Thể tích lớn nhất bằng \(150\) \({\rm{c}}{{\rm{m}}^3}\) khi \(a = b = 5\), tức là các cạnh đáy bằng $5$ cm.
Tính diện tích xung quanh của hình chóp cụt tứ giác đều có các cạnh đáy bằng $6cm$ và $8cm$ , chiều cao của mặt bên bằng $5cm$ .
-
A.
$120\,c{m^2}$
-
B.
$70\,c{m^2}$
-
C.
$150\,c{m^2}$
-
D.
$140\,c{m^2}$
Đáp án : D
Sử dụng công thức tính diện tích xung quanh hình chóp cụt đều
Để tính diện tích xung quanh của hình chóp cụt đều, ta tính diện tích một mặt bên rồi nhân với số mặt bên, hoặc lấy diện tích xung quanh của hình chóp đều lớn trừ đi diện tích xung quanh của hình chóp đều nhỏ.
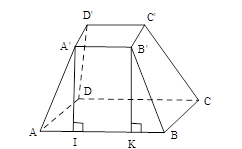
Mặt bên hình chóp cụt tứ giác đều là hình thang cân nên diện tích một mặt bên bằng \(\dfrac{{\left( {6 + 8} \right).5}}{2} = 35\,(c{m^2})\)
Hình chóp cụt tứ giác đều có \(4\) mặt bên bằng nhau nên diện tích xung quanh bằng $35.4 = 140\left( {c{m^2}} \right)$ .
>> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
 |
 |
 |
 |
 |
 |










Danh sách bình luận