Đề thi toán 9, đề kiểm tra toán 9 có đáp án và lời giải chi tiết

Đề kiểm tra học kì 1 Toán 9 - Đề số 1

Tổng hợp đề thi học kì 2 lớp 9 tất cả các môn

Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa - GDCD

Đề bài

Xem đáp án

Làm đề thi

Đề bài

Câu 1 :

Cho $a$ là số không âm, $b,c$ là số dương. Khẳng định nào sau đây là đúng?

A.

$\sqrt {\dfrac{a}{b}} = \dfrac{{\sqrt a }}{{\sqrt b }}$
B.

$\dfrac{{\sqrt {ab} }}{{\sqrt c }} = \sqrt {\dfrac{{ab}}{c}} $
C.

$\dfrac{{\sqrt a }}{{\sqrt {bc} }} = \dfrac{{\sqrt {ab} }}{{\sqrt c }}$
D.

Cả A, B đều đúng.

Câu 2 :

Điền vào các vị trí $\left( 1 \right);\left( 2 \right)$ trong bảng sau ($R$ là bán kính của đường tròn, $d$ là khoảng cách từ tâm đến đường thẳng) :

A.

$\left( 1 \right)$ : cắt nhau ; $\left( 2 \right)$ : $9\,cm$
B.

$\left( 1 \right)$ tiếp xúc nhau ; $\left( 2 \right)$ : $8\,cm$
C.

$\left( 1 \right)$ : không cắt nhau ; $\left( 2 \right)$ : $9\,cm$
D.

$\left( 1 \right)$ : không cắt nhau ; $\left( 2 \right)$ : $10\,cm$

Câu 3 :

Chọn khẳng định sai trong các khẳng định sau. Trong hai dây của một đường tròn

A.

Dây nào lớn hơn thì dây đó xa tâm hơn
B.

Dây nào nhỏ hơn thì dây đó xa tâm hơn
C.

Dây nào gần tâm hơn thì dây đó lớn hơn
D.

Hai dây bằng nhau thì cách đều tâm

Câu 4 :

Không dùng bảng số và máy tính, hãy so sánh $\sin 20^\circ $ và $\sin 70^\circ $

A.

$\sin 20^\circ < \sin 70^\circ $
B.

$\sin 20^\circ > \sin 70^\circ $
C.

$\sin 20^\circ = \sin 70^\circ $
D.

$\sin 20^\circ \ge \sin 70^\circ $

Câu 5 :

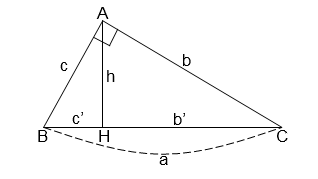
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$ (như hình vẽ). Hệ thức nào sau đây là sai?

A.

${b^2} = b'.a$
B.

$\dfrac{1}{{{h^2}}} = \dfrac{1}{{{c^2}}} + \dfrac{1}{{{b^2}}}$
C.

$a.h = b'.c'$
D.

${h^2} = b'.c'$

Câu 6 :

Chọn câu đúng. Bán kính của đường tròn ngoại tiếp tam giác vuông

A.

bằng cạnh nhỏ nhất của tam giác vuông
B.

bằng nửa cạnh góc vuông lớn hơn
C.

bằng nửa cạnh huyền
D.

bằng $4cm$

Câu 7 :

Giá trị của biểu thức $2\sqrt {32} - \sqrt {27} - 4\sqrt 8 + 3\sqrt {75} $ là:

A.

$16\sqrt 2 + 12\sqrt 3 $
B.

$15\sqrt 3 $
C.

$12\sqrt 3 $
D.

$16\sqrt 2 $

Câu 8 :

Cho tam giác $ABC$ vuông tại $A$ có $AC = 10\,cm,\widehat C = 30^\circ .$ Tính $AB;BC$

A.

$AB = \dfrac{{5\sqrt 3 }}{3};BC = \dfrac{{20\sqrt 3 }}{3}$
B.

$AB = \dfrac{{10\sqrt 3 }}{3};BC = \dfrac{{14\sqrt 3 }}{3}$
C.

$AB = \dfrac{{10\sqrt 3 }}{3};BC = 20\sqrt 3 $
D.

$AB = \dfrac{{10\sqrt 3 }}{3};BC = \dfrac{{20\sqrt 3 }}{3}$

Câu 9 :

Trong các hình vẽ sau, hình vẽ nào là đồ thị hàm số $y = 2x + 1$

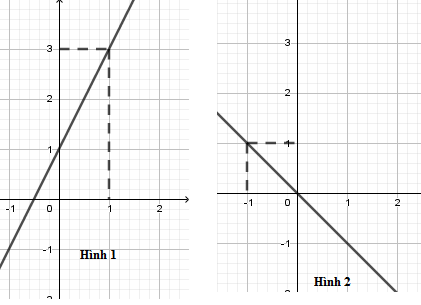
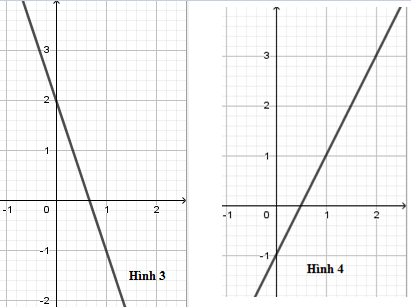
A.

Hình 4
B.

Hình 2
C.

Hình 3
D.

Hình 1

Câu 10 :

Tìm $m$ để hàm số $y = \dfrac{1}{{\sqrt {2m - 3} }}x + m$ là hàm số bậc nhất?

A.

$m < \dfrac{3}{2}$
B.

$m \ne \dfrac{3}{2}$
C.

$m = \dfrac{3}{2}$
D.

$m > \dfrac{3}{2}$

Câu 11 :

Cho $3$ điểm $A(0;3),B(2;2);C(m + 3;m)$. Giá trị của $m$ để $3$ điểm $A,B,C$ thẳng hàng là:

A.

$1$
B.

$ - 3$
C.

$3$
D.

$ - 1$

Câu 12 :

Kết quả của phép tính $\sqrt {\dfrac{{ - 999}}{{111}}} $ là?

A.

$9$
B.

$-9$
C.

$-3$
D.

Không tồn tại.

Câu 13 :

Số tâm đối xứng của đường tròn là:

A.

$1$
B.

$2$
C.

$3$
D.

$4$

Câu 14 :

Chọn đáp án đúng nhất. Với $a \ne 0$ hàm số $y = ax + b$ là hàm số

A.

Bậc nhất
B.

Hàm hằng
C.

Đồng biến
D.

Nghịch biến

Câu 15 :

Cho các biểu thức $A,B,C$ mà $A,B,C > 0$, khẳng định nào sau đây là đúng?

A.

$\sqrt {\dfrac{A}{{BC}}} = \dfrac{{\sqrt {ABC} }}{B}$
B.

$\sqrt {\dfrac{A}{B}} = - \dfrac{{\sqrt {ABC} }}{{BC}}$
C.

$\sqrt {\dfrac{A}{{BC}}} = \dfrac{{\sqrt {ABC} }}{{BC}}$
D.

$\sqrt {\dfrac{A}{{BC}}} = \dfrac{{ABC}}{{\sqrt {BC} }}$

Câu 16 :

Hai đường thẳng $d:y = ax + b\,\,\left( {a \ne 0} \right)$ và $d':y = a'x + b'\,\,\left( {a' \ne 0} \right)$ cắt nhau khi

A.

$a \ne a'$
B.

$\left\{ \begin{array}{l}a \ne a'\\b \ne b'\end{array} \right.$
C.

$\left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right.$
D.

$\left\{ \begin{array}{l}a \ne a'\\b = b'\end{array} \right.$

Câu 17 :

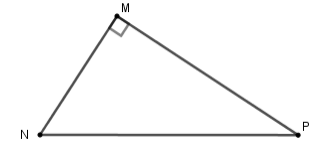
Cho tam giác $MNP$ vuông tại $M$. Khi đó $\tan \widehat {MNP}$ bằng

A.

$\dfrac{{MN}}{{NP}}$
B.

$\dfrac{{MP}}{{NP}}$
C.

$\dfrac{{MN}}{{MP}}$
D.

$\dfrac{{MP}}{{MN}}$

Câu 18 :

Cho đường tròn $\left( O \right)$ bán kính $OA$ và đường tròn $\left( {O'} \right)$ đường kính $OA$.

Câu 18.1

Vị trí tương đối của hai đường tròn là

A

Nằm ngoài nhau
B

Cắt nhau
C

Tiếp xúc ngoài
D

Tiếp xúc trong

Câu 18.2

Dây $AD$ của đường tròn lớn cắt đường tròn nhỏ tại $C$. Khi đó

A

$AC > CD$
B

$AC = CD$
C

$AC < CD$
D

$CD = OD$

Câu 19 :

Cho $3$ đường thẳng $\left( d \right):{\rm{ }}y = \left( {m + 2} \right)x - 3m;\left( {d'} \right):{\rm{ }}y = 2x + 4\;;\left( {d''} \right):{\rm{ }}y = - 3x - 1.$ Giá trị của $m$ để $3$ đường thẳng trên đồng quy là :

A.

$ - 1$
B.

$1$
C.

$2$
D.

$ - 2$

Câu 20 :

Cho biểu thức $P = \left( {\dfrac{{2x + 1}}{{\sqrt {{x^3}} - 1}} - \dfrac{1}{{\sqrt x - 1}}} \right):\left( {1 - \dfrac{{x + 4}}{{x + \sqrt x + 1}}} \right)$

Câu 20.1

Rút gọn P.

A

$P = \dfrac{{\sqrt x }}{{\sqrt x - 3}}$
B

$P = \dfrac{{\sqrt x }}{{\sqrt x + 3}}$
C

$P = \dfrac{{3 + \sqrt x }}{{\sqrt x - 3}}$
D

$P = \dfrac{{ - \sqrt x }}{{\sqrt x - 3}}$

Câu 20.2

Tìm các giá trị nguyên của x để P nhận giá trị nguyên dương.

A

$x = 1;x = 36$
B

$x = 16$
C

$x = 4;x = 6$
D

$x = 16; x = 36$

Câu 21 :

Cho tam giác $ABC$ vuông tại $A,$ đường cao $AH.$ Gọi $D$ và $E$ lần lượt là hình chiếu vuông góc của $H$ trên $AB, AC.$(hình vẽ)

Câu 21.1

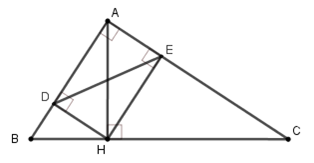
Tỉ số $\dfrac{{A{B^2}}}{{A{C^2}}}$ bằng với tỉ số nào sau đây?

A

$\dfrac{{A{B^2}}}{{A{C^2}}} = \dfrac{{HC}}{{HB}}$
B

$\dfrac{{A{B^2}}}{{A{C^2}}} = \dfrac{{HB}}{{HC}}$
C

$\dfrac{{A{B^2}}}{{A{C^2}}} = \dfrac{{HA}}{{HB}}$
D

$\dfrac{{A{B^2}}}{{A{C^2}}} = \dfrac{{HC}}{{HA}}$

Câu 21.2

Tỉ số $\dfrac{{A{B^3}}}{{A{C^3}}}$ bằng với tỉ số nào sau đây?

A

$\dfrac{{A{B^3}}}{{A{C^3}}} = \dfrac{{BD}}{{EC}}$
B

$\dfrac{{A{B^3}}}{{A{C^3}}} = \dfrac{{AD}}{{EC}}$
C

$\dfrac{{A{B^3}}}{{A{C^3}}} = \dfrac{{BD}}{{ED}}$
D

$\dfrac{{A{B^3}}}{{A{C^3}}} = \dfrac{{EC}}{{BD}}$

Câu 22 :

Chọn kết luận đúng về nghiệm ${x_0}$ (nếu có) của phương trình: $\dfrac{{8 + 3x}}{{\sqrt {2x - 5} }} = \sqrt {2x - 5} $.

A.

${x_0} > 3$
B.

${x_0} = - 13$
C.

${x_0} \in \emptyset $
D.

${x_0} = 13$

Câu 23 :

Tính giá trị biểu thức$\left( {\dfrac{{\sqrt {14} - \sqrt 7 }}{{1 - \sqrt 2 }} + \dfrac{{\sqrt {15} - \sqrt 5 }}{{1 - \sqrt 3 }}} \right):\dfrac{1}{{\sqrt 7 - \sqrt 5 }}.$

A.

$ - 3$
B.

$ - 2$
C.

$2$
D.

$3$

Câu 24 :

Cho biểu thức $P = \dfrac{x}{{\sqrt x + 1}}$. Giá trị của $P$ khi $x = \dfrac{2}{{2 - \sqrt 3 }}$ là

A.

$4$
B.

$2$
C.

$3$
D.

$1$

Câu 25 :

Gọi ${d_1}$ là đồ thị hàm số $y = - \left( {2m - 2} \right)x + 4m$ và ${d_2}$ là đồ thị hàm số $y = 4x - 1$. Xác định giá trị của $m$ để $M\left( {1;3} \right)$ là giao điểm của ${d_1}$ và ${d_2}$.

A.

$m = \dfrac{1}{2}$
B.

$m = - \dfrac{1}{2}$
C.

$m = 2$
D.

$m = - 2$

Câu 26 :

Viết phương trình đường thẳng $d$ biết $d$ đi qua hai điểm $A\left( {3;3} \right);B\left( { - 1;4} \right)$

A.

$y = \dfrac{1}{4}x - \dfrac{{15}}{4}$
B.

$y = - \dfrac{1}{4}x + \dfrac{{15}}{4}$
C.

$y = - \dfrac{1}{4}x - \dfrac{{15}}{4}$
D.

$y = \dfrac{1}{4}x + \dfrac{{15}}{4}$

Câu 27 :

Viết phương trình đường thẳng $d$ biết $d$ tạo với trục $Ox$ một góc bằng $30^\circ $ và cắt trục hoành tại điểm có hoành độ bằng $6$.

A.

$y = \dfrac{{\sqrt 3 }}{3}x$
B.

$y = \dfrac{{\sqrt 3 }}{3}x + 2\sqrt 3 $
C.

$y = \dfrac{{\sqrt 3 }}{3}x - 2\sqrt 3 $
D.

$y = \sqrt 3 x - 2\sqrt 3 $

Câu 28 :

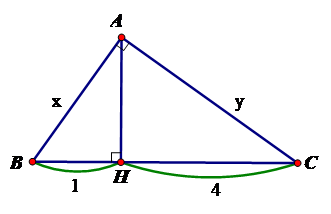
Tính $x,y$ trong hình vẽ sau:

A.

$x = 2\sqrt 5 ;y = \sqrt 5 $
B.

$x = \sqrt 5 ;y = 3\sqrt 5 $
C.

$x = \sqrt 5 ;y = 2\sqrt 5 $
D.

$x = 2\sqrt 5 ;y = 2\sqrt 5 $

Câu 29 :

Chọn kết luận đúng về giá trị biểu thức $B = \dfrac{{{{\cos }^2}\alpha - 3{{\sin }^2}\alpha }}{{3 - {{\sin }^2}\alpha }}$ biết $\tan \alpha = 3.$

A.

$B > 0$
B.

$B < 0$
C.

$0 < B < 1$
D.

$B = 1$

Câu 30 :

Một cái cây bị sét đánh trúng thân cây làm thân cây ngả xuống đất, tạo với mặt đất một góc là ${40^0}$. Biết rằng khúc cây còn đứng cao $1\,m$ . Tính chiều cao lúc đầu của cây.

A.

$2,61\,m$
B.

$2,81\,m$
C.

$2,58\,m$
D.

$2,56\,m$

Câu 31 :

Cho hình vuông $ABCD$. Gọi $M,N$ lần lượt là trung điểm của $AB,BC$ . Gọi $E$ là giao điểm của $CM$ và $DN$. Tâm của đường tròn đi qua bốn điểm $A,D,E,M$ là

A.

Trung điểm của $DM$.
B.

Trung điểm của $DB$.
C.

Trung điểm của $DE$.
D.

Trung điểm của $DA$.

Câu 32 :

Cho đường tròn $\left( {O;R} \right)$ có hai dây $AB,CD$ vuông góc với nhau ở $M$. Biết$\,CD = 8\,cm;\,MC = 1\,cm$. Khoảng cách từ tâm $O$ đến dây $AB$ là

A.

$4\,cm$
B.

$5\,cm$
C.

$3\,cm$
D.

$2\,cm$

Câu 33 :

Cho tam giác $ABC$ cân tại $A$; đường cao $AH$ và $BK$ cắt nhau tại $I$. Khi đó đường thẳng nào sau đây là tiếp tuyến của đường tròn đường kính $AI$.

A.

$HK$
B.

$IB$
C.

$IC$
D.

$AC$

Câu 34 :

Trên mặt phẳng tọa độ $Oxy$, cho điểm $A\left( {4;5} \right)$. Hãy xác định vị trí tương đối của đường tròn $\left( {A;5} \right)$ và các trục tọa độ.

A.

Trục tung cắt đường tròn và trục hoành tiếp xúc với đường tròn.
B.

Trục hoành cắt đường tròn và trục tung tiếp xúc với đường tròn
C.

Cả hai trục tọa độ đều cắt đường tròn
D.

Cả hai trục tọa độ đều tiếp xúc với đường tròn.

Câu 35 :

Cho đường tròn $(O).$ Từ một điểm $M$ ở ngoài $(O)$, vẽ hai tiếp tuyến $MA$ và $MB$ sao cho góc $AMB$ bằng ${60^0}$. Biết chu vi tam giác $MAB$ là $24\,cm$, tính độ dài bán kính đường tròn.

A.

$8\,cm$
B.

$\,8\sqrt 3\,cm$
C.

$\dfrac {8}{\sqrt 3}\,cm$
D.

$5\,cm$

Câu 36 :

Cho đường thẳng $d:y = x + 2;d':y = - 2x + 5$. Gọi $M$ là giao điểm của $d$ và $d'$ . $A$ và $B$ lần lượt là giao điểm của $d$ và $d'$ với trục hoành. Khi đó diện tích tam giác $AMB$ là:

A.

$\dfrac{{27}}{6}$ ( đvdt)
B.

$27$( đvdt)
C.

$\dfrac{{27}}{2}$ (đvdt)
D.

$\dfrac{{27}}{4}$(đvdt)

Câu 37 :

Cho tam giác nhọn $ABC$ hai đường cao $AD$ và $BE$ cắt nhau tại $H$. Biết $HD:HA = 1:2$. Tính $\tan B.\tan C$

A.

$\dfrac{1}{2}$
B.

$\dfrac{1}{3}$
C.

$2$
D.

$3$

Lời giải và đáp án

Câu 1 :

Cho $a$ là số không âm, $b,c$ là số dương. Khẳng định nào sau đây là đúng?

A.

$\sqrt {\dfrac{a}{b}} = \dfrac{{\sqrt a }}{{\sqrt b }}$
B.

$\dfrac{{\sqrt {ab} }}{{\sqrt c }} = \sqrt {\dfrac{{ab}}{c}} $
C.

$\dfrac{{\sqrt a }}{{\sqrt {bc} }} = \dfrac{{\sqrt {ab} }}{{\sqrt c }}$
D.

Cả A, B đều đúng.

Đáp án : D

Lời giải chi tiết :

Với số $a$ không âm và số $b$ dương , ta có $\sqrt {\dfrac{a}{b}} = \dfrac{{\sqrt a }}{{\sqrt b }}$

Từ đó suy ra $\dfrac{{\sqrt {ab} }}{{\sqrt c }} = \sqrt {\dfrac{{ab}}{c}} $ với $c > 0.$

Câu 2 :

Điền vào các vị trí $\left( 1 \right);\left( 2 \right)$ trong bảng sau ($R$ là bán kính của đường tròn, $d$ là khoảng cách từ tâm đến đường thẳng) :

A.

$\left( 1 \right)$ : cắt nhau ; $\left( 2 \right)$ : $9\,cm$
B.

$\left( 1 \right)$ tiếp xúc nhau ; $\left( 2 \right)$ : $8\,cm$
C.

$\left( 1 \right)$ : không cắt nhau ; $\left( 2 \right)$ : $9\,cm$
D.

$\left( 1 \right)$ : không cắt nhau ; $\left( 2 \right)$ : $10\,cm$

Đáp án : C

Phương pháp giải :

Sử dụng bảng vị trí tương đối của đường thẳng và đường tròn

Lời giải chi tiết :

+) Vì $d > R\left( {5\,cm < 3\,cm} \right)$ nên đường thẳng không cắt đường tròn hay (1) điền là: Không cắt nhau.

+) Vì đường thẳng tiếp xúc với đường tròn nên $d = R = 9\,cm$ hay (2) điền là $9\,cm$

Câu 3 :

Chọn khẳng định sai trong các khẳng định sau. Trong hai dây của một đường tròn

A.

Dây nào lớn hơn thì dây đó xa tâm hơn
B.

Dây nào nhỏ hơn thì dây đó xa tâm hơn
C.

Dây nào gần tâm hơn thì dây đó lớn hơn
D.

Hai dây bằng nhau thì cách đều tâm

Đáp án : A

Lời giải chi tiết :

- Trong một đường tròn:

+ Hai dây bằng nhau thì cách đều tâm.

- Trong hai dây của một đường tròn:

+ Dây nào lớn hơn thì dây đó gần tâm hơn.

+ Dây nào gần tâm hơn thì dây đó lớn hơn,

Nên phương án B,C,D đúng.

Câu 4 :

Không dùng bảng số và máy tính, hãy so sánh $\sin 20^\circ $ và $\sin 70^\circ $

A.

$\sin 20^\circ < \sin 70^\circ $
B.

$\sin 20^\circ > \sin 70^\circ $
C.

$\sin 20^\circ = \sin 70^\circ $
D.

$\sin 20^\circ \ge \sin 70^\circ $

Đáp án : A

Phương pháp giải :

Sử dụng nhận xét : Với góc nhọn $\alpha ,\,\beta ,$ ta có: $\sin \alpha < \sin \beta \Leftrightarrow \alpha < \beta $

Lời giải chi tiết :

Vì $20^\circ < 70^\circ \Leftrightarrow \sin 20^\circ < \sin 70^\circ $.

Câu 5 :

Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$ (như hình vẽ). Hệ thức nào sau đây là sai?

A.

${b^2} = b'.a$
B.

$\dfrac{1}{{{h^2}}} = \dfrac{1}{{{c^2}}} + \dfrac{1}{{{b^2}}}$
C.

$a.h = b'.c'$
D.

${h^2} = b'.c'$

Đáp án : C

Lời giải chi tiết :

Nhận thấy $ah = bc$ nên phương án C là sai.

Câu 6 :

Chọn câu đúng. Bán kính của đường tròn ngoại tiếp tam giác vuông

A.

bằng cạnh nhỏ nhất của tam giác vuông
B.

bằng nửa cạnh góc vuông lớn hơn
C.

bằng nửa cạnh huyền
D.

bằng $4cm$

Đáp án : C

Phương pháp giải :

Sử dụng nhận xét: “ Trong tam giác vuông trung điểm cạnh huyền là tâm đường tròn ngoại tiếp” từ đó suy ra bán kính của đường tròn ngoại tiếp.

Lời giải chi tiết :

Trong tam giác vuông trung điểm cạnh huyền là tâm đường tròn ngoại tiếp. Do đó bán kính đường tròn ngoại tiếp tam giác vuông bằng nửa cạnh huyền.

Câu 7 :

Giá trị của biểu thức $2\sqrt {32} - \sqrt {27} - 4\sqrt 8 + 3\sqrt {75} $ là:

A.

$16\sqrt 2 + 12\sqrt 3 $
B.

$15\sqrt 3 $
C.

$12\sqrt 3 $
D.

$16\sqrt 2 $

Đáp án : C

Phương pháp giải :

- Sử dụng công thức khai phương một tích $\sqrt {AB} = \sqrt A .\sqrt B ,\,\,\left( {A,B \ge 0} \right)$ đưa biểu thức về các căn thức cùng loại (cùng biểu thức dưới dấu căn).

- Sử dụng $\sqrt {{A^2}B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,khi\,A \ge 0\\ - A\sqrt B \,khi\,A < 0\end{array} \right.$

- Cộng trừ các căn thức.

Lời giải chi tiết :

$2\sqrt {32} - \sqrt {27} - 4\sqrt 8 + 3\sqrt {75} $$ = 2\sqrt {16.2} - \sqrt {9.3} - 4\sqrt {4.2} + 3\sqrt {25.3} $$= 8\sqrt 2 - 3\sqrt 3 - 8\sqrt 2 + 15\sqrt 3 = 12\sqrt 3 $

Câu 8 :

Cho tam giác $ABC$ vuông tại $A$ có $AC = 10\,cm,\widehat C = 30^\circ .$ Tính $AB;BC$

A.

$AB = \dfrac{{5\sqrt 3 }}{3};BC = \dfrac{{20\sqrt 3 }}{3}$
B.

$AB = \dfrac{{10\sqrt 3 }}{3};BC = \dfrac{{14\sqrt 3 }}{3}$
C.

$AB = \dfrac{{10\sqrt 3 }}{3};BC = 20\sqrt 3 $
D.

$AB = \dfrac{{10\sqrt 3 }}{3};BC = \dfrac{{20\sqrt 3 }}{3}$

Đáp án : D

Lời giải chi tiết :

Xét tam giác $ABC$ vuông tại $A$ có

$\tan C = \dfrac{{AB}}{{AC}} \Rightarrow AB = AC.\tan C = 10.\tan 30^\circ = \dfrac{{10\sqrt 3 }}{3}$; $\cos C = \dfrac{{AC}}{{BC}} \Rightarrow BC = \dfrac{{AC}}{{\cos C}} = \dfrac{{10}}{{\dfrac{{\sqrt 3 }}{2}}} = \dfrac{{20\sqrt 3 }}{3}$

Vậy $AB = \dfrac{{10\sqrt 3 }}{3};BC = \dfrac{{20\sqrt 3 }}{3}$.

Câu 9 :

Trong các hình vẽ sau, hình vẽ nào là đồ thị hàm số $y = 2x + 1$

A.

Hình 4
B.

Hình 2
C.

Hình 3
D.

Hình 1

Đáp án : D

Phương pháp giải :

Sử dụng cách vẽ đồ thị hàm số

Đồ thị hàm số $y = ax + b\,\,\left( {a \ne 0} \right)$ là một đường thẳng

Nếu $b \ne 0$ thì đồ thị $y = ax + b$ là đường thẳng đi qua các điểm $A(0;b),\,\,B\left( { - \dfrac{b}{a};0} \right).$

Lời giải chi tiết :

Đồ thị hàm số $y = 2x + 1$ là đường thẳng đi qua hai điểm có tọa độ $\left( {0;1} \right)$ và $\left( {1;3} \right)$ nên hình 1 là đồ thị hàm số $y = 2x + 1$.

Câu 10 :

Tìm $m$ để hàm số $y = \dfrac{1}{{\sqrt {2m - 3} }}x + m$ là hàm số bậc nhất?

A.

$m < \dfrac{3}{2}$
B.

$m \ne \dfrac{3}{2}$
C.

$m = \dfrac{3}{2}$
D.

$m > \dfrac{3}{2}$

Đáp án : D

Phương pháp giải :

Sử dụng định nghĩa hàm số bậc nhất

Hàm số bậc nhất là hàm số dạng $y = ax + b\,\,\left( {a \ne 0} \right)$

Lời giải chi tiết :

Hàm số $y = \dfrac{1}{{\sqrt {2m - 3} }}x + m$ là hàm số bậc nhất khi $\left\{ \begin{array}{l}\dfrac{1}{{\sqrt {2m - 3} }}>0\\\sqrt {2m - 3} \ne 0\end{array} \right. \Leftrightarrow 2m - 3 > 0 \Leftrightarrow m > \dfrac{3}{2}.$

Câu 11 :

Cho $3$ điểm $A(0;3),B(2;2);C(m + 3;m)$. Giá trị của $m$ để $3$ điểm $A,B,C$ thẳng hàng là:

A.

$1$
B.

$ - 3$
C.

$3$
D.

$ - 1$

Đáp án : A

Phương pháp giải :

- Viết phương trình đường thẳng $(d)$ đi qua 2 điểm cho trước $A;B$.

- Để $3$ điểm $A;B;C$ thẳng hàng thì $C \in (d)$

Lời giải chi tiết :

Gọi $d:y = {\rm{ax}} + b$ là đường thẳng đi qua $A$ và $B$.

$\begin{array}{l}A(0;3) \in d \Leftrightarrow a.0 + b = 3 \Leftrightarrow b = 3\\B(2;2) \in d \Leftrightarrow a.2 + b = 2\\ \Rightarrow \left\{ \begin{array}{l}b = 3\\2a + b = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 3\\a = - \dfrac{1}{2}\end{array} \right. \Rightarrow d:y = - \dfrac{1}{2}x + 3\end{array}$

Để $3$ điểm $A,B,C$ thẳng hàng thì $C(m + 3;m) \in (d):y = - \dfrac{1}{2}x + 3$

$ \Leftrightarrow m = - \dfrac{1}{2}\left( {m + 3} \right) + 3 \Leftrightarrow \dfrac{3}{2}m = \dfrac{3}{2} \Leftrightarrow m = 1$.

Vậy $m = 1$.

Câu 12 :

Kết quả của phép tính $\sqrt {\dfrac{{ - 999}}{{111}}} $ là?

A.

$9$
B.

$-9$
C.

$-3$
D.

Không tồn tại.

Đáp án : D

Phương pháp giải :

Sử dụng công thức khai phương một thương: Với số $a$ không âm và số $b$ dương , ta có $\sqrt {\dfrac{a}{b}} = \dfrac{{\sqrt a }}{{\sqrt b }}$.

Lời giải chi tiết :

Vì $ - 999 < 0;111 > 0 \Rightarrow \dfrac{{ - 999}}{{111}} < 0$ nên không tồn tại căn bậc hai của số âm

Câu 13 :

Số tâm đối xứng của đường tròn là:

A.

$1$
B.

$2$
C.

$3$
D.

$4$

Đáp án : A

Lời giải chi tiết :

Đường tròn là hình có tâm đối xứng. Tâm đường tròn là tâm đối xứng của đường tròn đó.

Nên đường tròn có một tâm đối xứng duy nhất là tâm của đường tròn.

Câu 14 :

Chọn đáp án đúng nhất. Với $a \ne 0$ hàm số $y = ax + b$ là hàm số

A.

Bậc nhất
B.

Hàm hằng
C.

Đồng biến
D.

Nghịch biến

Đáp án : A

Lời giải chi tiết :

Hàm số có dạng $y = ax + b\,\,\left( {a \ne 0} \right)$ là hàm số bậc nhất.

Câu 15 :

Cho các biểu thức $A,B,C$ mà $A,B,C > 0$, khẳng định nào sau đây là đúng?

A.

$\sqrt {\dfrac{A}{{BC}}} = \dfrac{{\sqrt {ABC} }}{B}$
B.

$\sqrt {\dfrac{A}{B}} = - \dfrac{{\sqrt {ABC} }}{{BC}}$
C.

$\sqrt {\dfrac{A}{{BC}}} = \dfrac{{\sqrt {ABC} }}{{BC}}$
D.

$\sqrt {\dfrac{A}{{BC}}} = \dfrac{{ABC}}{{\sqrt {BC} }}$

Đáp án : C

Phương pháp giải :

Sử dụng công thức khử mẫu của biểu thức lấy căn.

Với các biểu thức $A,B$ mà $A.B \ge 0;B \ne 0$, ta có: $\sqrt {\dfrac{A}{B}} = \dfrac{{\sqrt {AB} }}{{\left| B \right|}} = \left\{ \begin{array}{l}\dfrac{{\sqrt {AB} }}{B}\,\,khi\,B > 0\\ - \dfrac{{\sqrt {AB} }}{B}\,\,khi\,B < 0\end{array} \right.$

Lời giải chi tiết :

Với các biểu thức $A,B,C$ mà $A,B,C > 0$, ta có: $\sqrt {\dfrac{A}{{BC}}} = \dfrac{{\sqrt {ABC} }}{{\left| {BC} \right|}} = \dfrac{{\sqrt {ABC} }}{{BC}}$ (vì $B,C > 0$)

Câu 16 :

Hai đường thẳng $d:y = ax + b\,\,\left( {a \ne 0} \right)$ và $d':y = a'x + b'\,\,\left( {a' \ne 0} \right)$ cắt nhau khi

A.

$a \ne a'$
B.

$\left\{ \begin{array}{l}a \ne a'\\b \ne b'\end{array} \right.$
C.

$\left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right.$
D.

$\left\{ \begin{array}{l}a \ne a'\\b = b'\end{array} \right.$

Đáp án : A

Lời giải chi tiết :

Cho hai đường thẳng $d:y = ax + b\,\,\left( {a \ne 0} \right)$ và $d':y = a'x + b'\,\,\left( {a' \ne 0} \right)$.

$d$ cắt $d'$$ \Leftrightarrow a \ne a'$.

Câu 17 :

Cho tam giác $MNP$ vuông tại $M$. Khi đó $\tan \widehat {MNP}$ bằng

A.

$\dfrac{{MN}}{{NP}}$
B.

$\dfrac{{MP}}{{NP}}$
C.

$\dfrac{{MN}}{{MP}}$
D.

$\dfrac{{MP}}{{MN}}$

Đáp án : D

Lời giải chi tiết :

Ta có $\tan \widehat {MNP} = \dfrac{{MP}}{{NN}}$

Câu 18 :

Cho đường tròn $\left( O \right)$ bán kính $OA$ và đường tròn $\left( {O'} \right)$ đường kính $OA$.

Câu 18.1

Vị trí tương đối của hai đường tròn là

A

Nằm ngoài nhau
B

Cắt nhau
C

Tiếp xúc ngoài
D

Tiếp xúc trong

Đáp án: D

Lời giải chi tiết :

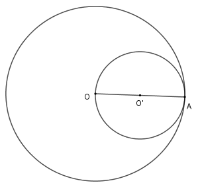
Vì hai đường tròn có một điểm chung là $A$ và $OO' = OA - \dfrac{{OA}}{2} = R - r$ nên hai đường tròn tiếp xúc trong.

Câu 18.2

Dây $AD$ của đường tròn lớn cắt đường tròn nhỏ tại $C$. Khi đó

A

$AC > CD$
B

$AC = CD$
C

$AC < CD$
D

$CD = OD$

Đáp án: B

Phương pháp giải :

Sử dụng tính chất tam giác cân.

Lời giải chi tiết :

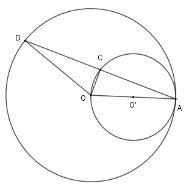
Xét đường tròn $\left( {O'} \right)$ có $OA$ là đường kính và $C \in \left( {O'} \right)$ nên $\Delta ACO$ vuông tại $C$ hay $OC \bot AD$

Xét đường tròn $\left( O \right)$có $OA = OD \Rightarrow \Delta OAD$ cân tại $O$ có $OC$ là đường cao cũng là đường trung tuyến nên $CD = CA$

Câu 19 :

A.

$ - 1$
B.

$1$
C.

$2$
D.

$ - 2$

Đáp án : A

Phương pháp giải :

- Tìm tọa độ giao điểm 2 đường thẳng cho trước $d';d''$

- Cho giao điểm vừa tìm được thuộc vào đường thẳng $d$.

Điểm $M\left( {{x_0};{y_0}} \right)$ thuộc đường thẳng $\left( d \right):y = ax + b $$\Leftrightarrow {y_0} = a{x_0} + b$

Lời giải chi tiết :

Xét phương trình hoành độ giao điểm $A$ của $\left( {d'} \right)$ và $\left( {d''} \right)$:

$\begin{array}{*{20}{l}}{2x + 4 = - 3x - 1}\\{ \Leftrightarrow 5x = - 5}\\{ \Leftrightarrow x = - 1}\\{ \Rightarrow y = 2\left( { - 1} \right) + 4 = 2}\\{ \Rightarrow A\left( { - 1;2} \right)}\end{array}$

Để $\left( d \right);\left( {d'} \right);\left( {d''} \right)$ đồng quy thì $A\left( { - 1;2} \right) \in \left( d \right)$

$\begin{array}{*{20}{l}}{ \Leftrightarrow 2 = \left( {m + 2} \right).\left( { - 1} \right) - 3m}\\{ \Leftrightarrow 2 = - 2 - 4m}\\{ \Leftrightarrow 4m = - 4}\\{ \Leftrightarrow m = - 1}\end{array}$

Vậy khi $m = - 1$ thì $\left( d \right);\left( {d'} \right);\left( {d''} \right)$ đồng quy tại $A\left( { - 1;2} \right)$.

Câu 20 :

Cho biểu thức $P = \left( {\dfrac{{2x + 1}}{{\sqrt {{x^3}} - 1}} - \dfrac{1}{{\sqrt x - 1}}} \right):\left( {1 - \dfrac{{x + 4}}{{x + \sqrt x + 1}}} \right)$

Câu 20.1

Rút gọn P.

A

$P = \dfrac{{\sqrt x }}{{\sqrt x - 3}}$
B

$P = \dfrac{{\sqrt x }}{{\sqrt x + 3}}$
C

$P = \dfrac{{3 + \sqrt x }}{{\sqrt x - 3}}$
D

$P = \dfrac{{ - \sqrt x }}{{\sqrt x - 3}}$

Đáp án: A

Phương pháp giải :

- Tìm mẫu thức chung bằng cách phân tích đa thức thành nhân tử.

- Quy đồng mẫu thức các phân thức.

- Cộng trừ các phân thức đã quy đồng và rút gọn.

Lời giải chi tiết :

ĐKXĐ: $\left\{ \begin{array}{l}x \ge 0\\x \ne 1\end{array} \right.$

$\begin{array}{l}P = \left( {\dfrac{{2x + 1}}{{\sqrt {{x^3}} - 1}} - \dfrac{1}{{\sqrt x - 1}}} \right):\left( {1 - \dfrac{{x + 4}}{{x + \sqrt x + 1}}} \right)\\ = \left( {\dfrac{{2x + 1}}{{\left( {\sqrt x - 1} \right)\left( {x + \sqrt x + 1} \right)}} - \dfrac{1}{{\sqrt x - 1}}} \right):\left( {\dfrac{{x + \sqrt x + 1 - x - 4}}{{x + \sqrt x + 1}}} \right)\\ = \dfrac{{2x + 1 - x - \sqrt x - 1}}{{\left( {\sqrt x - 1} \right)\left( {x + \sqrt x + 1} \right)}}:\dfrac{{\sqrt x - 3}}{{x + \sqrt x + 1}}\\ = \dfrac{{x - \sqrt x }}{{\left( {\sqrt x - 1} \right)\left( {x + \sqrt x + 1} \right)}}.\dfrac{{x + \sqrt x + 1}}{{\sqrt x - 3}}\,\,\,\,\left( {x \ne 9} \right)\\ = \dfrac{{\sqrt x \left( {\sqrt x - 1} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x - 3} \right)}} = \dfrac{{\sqrt x }}{{\sqrt x - 3}}.\end{array}$

Vậy $P = \dfrac{{\sqrt x }}{{\sqrt x - 3}}$ với $x \ge 0;x \ne 1;x \ne 9$

Câu 20.2

Tìm các giá trị nguyên của x để P nhận giá trị nguyên dương.

A

$x = 1;x = 36$
B

$x = 16$
C

$x = 4;x = 6$
D

$x = 16; x = 36$

Đáp án: D

Phương pháp giải :

Sử dụng kết quả câu trước $P = \dfrac{{\sqrt x }}{{\sqrt x - 3}}$ với $x \ge 0;x \ne 1;x \ne 9$

Đưa P về dạng $P = a + \dfrac{m}{{\sqrt x - 3}}\left( {a;m \in \mathbb{Z}} \right)$, khi đó để $P$ nhận giá trị là số nguyên dương thì $\left\{ \begin{array}{l}P \in \mathbb{Z}\\P > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\dfrac{m}{{\sqrt x - 3}} \in \mathbb{Z}\\a + \dfrac{m}{{\sqrt x - 3}} > 0\end{array} \right.$

Lời giải chi tiết :

ĐKXĐ: $\left\{ \begin{array}{l}x \ge 0\\x \ne 1\\x \ne 9\end{array} \right.$

Ta có: $P = \dfrac{{\sqrt x }}{{\sqrt x - 3}} = \dfrac{{\sqrt x - 3 + 3}}{{\sqrt x - 3}} = 1 + \dfrac{3}{{\sqrt x - 3}}.$

Để $P$ nhận giá trị là số nguyên dương thì $\left\{ \begin{array}{l}P \in \mathbb{Z}\\P > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\dfrac{3}{{\sqrt x - 3}} \in \mathbb{Z}\\1 + \dfrac{3}{{\sqrt x - 3}} > 0\end{array} \right.$

$\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}\dfrac{3}{{\sqrt x - 3}} \in Z\\\dfrac{3}{{\sqrt x - 3}} > - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\dfrac{3}{{\sqrt x - 3}} \in Z\\\dfrac{{3 + \sqrt x - 3}}{{\sqrt x - 3}} > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left( {\sqrt x - 3} \right) \in U\left( 3 \right)(1)\\\dfrac{{\sqrt x }}{{\sqrt x - 3}} > 0(2)\end{array} \right.\\(1) \Leftrightarrow \left( {\sqrt x - 3} \right) \in \left\{ {1;\,\,3} \right\}\\ \Leftrightarrow \left[ \begin{array}{l}\sqrt x - 3 = 1\\\sqrt x - 3 = 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\sqrt x = 4\\\sqrt x = 6\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 16\,\,\left( {tm} \right)\\x = 36\,\,\left( {tm} \right)\end{array} \right.\end{array}$

Vậy x = 16 hoặc x = 36 thì P nguyên dương.

Câu 21 :

Cho tam giác $ABC$ vuông tại $A,$ đường cao $AH.$ Gọi $D$ và $E$ lần lượt là hình chiếu vuông góc của $H$ trên $AB, AC.$(hình vẽ)

Câu 21.1

Tỉ số $\dfrac{{A{B^2}}}{{A{C^2}}}$ bằng với tỉ số nào sau đây?

A

$\dfrac{{A{B^2}}}{{A{C^2}}} = \dfrac{{HC}}{{HB}}$
B

$\dfrac{{A{B^2}}}{{A{C^2}}} = \dfrac{{HB}}{{HC}}$
C

$\dfrac{{A{B^2}}}{{A{C^2}}} = \dfrac{{HA}}{{HB}}$
D

$\dfrac{{A{B^2}}}{{A{C^2}}} = \dfrac{{HC}}{{HA}}$

Đáp án: B

Lời giải chi tiết :

Xét tam giác vuông $ABC$ có $AH$ là đường cao nên $A{B^2} = BH.BC;A{C^2} = CH.BC$

Nên $\dfrac{{A{B^2}}}{{A{C^2}}} = \dfrac{{BH.BC}}{{CH.BC}} = \dfrac{{HB}}{{HC}}$

Câu 21.2

Tỉ số $\dfrac{{A{B^3}}}{{A{C^3}}}$ bằng với tỉ số nào sau đây?

A

$\dfrac{{A{B^3}}}{{A{C^3}}} = \dfrac{{BD}}{{EC}}$
B

$\dfrac{{A{B^3}}}{{A{C^3}}} = \dfrac{{AD}}{{EC}}$
C

$\dfrac{{A{B^3}}}{{A{C^3}}} = \dfrac{{BD}}{{ED}}$
D

$\dfrac{{A{B^3}}}{{A{C^3}}} = \dfrac{{EC}}{{BD}}$

Đáp án: A

Lời giải chi tiết :

Tam giác vuông $AHB$ có $B{H^2} = BD.AB \Rightarrow BD = \dfrac{{B{H^2}}}{{AB}}$

Tam giác vuông $AHC$ có $H{C^2} = AC.EC \Rightarrow EC = \dfrac{{H{C^2}}}{{AC}}$

Từ đó $\dfrac{{BD}}{{EC}} = \dfrac{{H{B^2}}}{{AB}}:\dfrac{{H{C^2}}}{{AC}} = \dfrac{{H{B^2}}}{{H{C^2}}}.\dfrac{{AC}}{{AB}}$ mà theo câu trước thì $\dfrac{{A{B^2}}}{{A{C^2}}} = \dfrac{{HB}}{{HC}}$ nên $\dfrac{{BD}}{{EC}} = \dfrac{{A{B^4}}}{{A{C^4}}}.\dfrac{{AC}}{{AB}} \Leftrightarrow \dfrac{{BD}}{{EC}} = \dfrac{{A{B^3}}}{{A{C^3}}}$

Câu 22 :

Chọn kết luận đúng về nghiệm ${x_0}$ (nếu có) của phương trình: $\dfrac{{8 + 3x}}{{\sqrt {2x - 5} }} = \sqrt {2x - 5} $.

A.

${x_0} > 3$
B.

${x_0} = - 13$
C.

${x_0} \in \emptyset $
D.

${x_0} = 13$

Đáp án : C

Phương pháp giải :

- Tìm điều kiện xác định.

- Sử dụng hằng đẳng thức ${\left( {\sqrt A } \right)^2} = A$ khi $A > 0$ để đưa phương trình về dạng đã biết.

- So sánh điều kiện rồi kết luận nghiệm.

Lời giải chi tiết :

Điều kiện: $2x - 5 > 0 \Leftrightarrow x > \dfrac{5}{2}$

Với điều kiện trên ta có: $\dfrac{{8 + 3x}}{{\sqrt {2x - 5} }} = \sqrt {2x - 5} $$ \Rightarrow 8 + 3x = {\left( {\sqrt {2x - 5} } \right)^2} \Leftrightarrow 8 + 3x = 2x - 5$$\Leftrightarrow x = -13\,\left( {KTM} \right)$

Vậy phương trình vô nghiệm.

Câu 23 :

Tính giá trị biểu thức$\left( {\dfrac{{\sqrt {14} - \sqrt 7 }}{{1 - \sqrt 2 }} + \dfrac{{\sqrt {15} - \sqrt 5 }}{{1 - \sqrt 3 }}} \right):\dfrac{1}{{\sqrt 7 - \sqrt 5 }}.$

A.

$ - 3$
B.

$ - 2$
C.

$2$
D.

$3$

Đáp án : B

Phương pháp giải :

- Sử dụng công thức khai phương một tích để xuất hiện nhân tử chung và rút gọn

$\sqrt {AB} = \sqrt A .\sqrt B \,\,\left( {A,B \ge 0} \right)$

- Hoặc trục căn thức ở mẫu rồi rút gọn

Với các biểu thức $A,B,C$ mà $A \ge 0,A \ne {B^2}$, ta có $\dfrac{C}{{\sqrt A + B}} = \dfrac{{C\left( {\sqrt A - B} \right)}}{{A - {B^2}}};\dfrac{C}{{\sqrt A - B}} = \dfrac{{C\left( {\sqrt A + B} \right)}}{{A - {B^2}}}$

Lời giải chi tiết :

Ta có $\left( {\dfrac{{\sqrt {14} - \sqrt 7 }}{{1 - \sqrt 2 }} + \dfrac{{\sqrt {15} - \sqrt 5 }}{{1 - \sqrt 3 }}} \right):\dfrac{1}{{\sqrt 7 - \sqrt 5 }}$$ = \left( {\dfrac{{\sqrt 2 .\sqrt 7 - \sqrt 7 }}{{1 - \sqrt 2 }} + \dfrac{{\sqrt 5 .\sqrt 3 - \sqrt 5 }}{{1 - \sqrt 3 }}} \right):\dfrac{1}{{\sqrt 7 - \sqrt 5 }}$

$ = \left( {\dfrac{{\sqrt 7 \left( {\sqrt 2 - 1} \right)}}{{1 - \sqrt 2 }} + \dfrac{{\sqrt 5 \left( {\sqrt 3 - 1} \right)}}{{1 - \sqrt 3 }}} \right).\left( {\sqrt 7 - \sqrt 5 } \right)$

$ = \left( { - \sqrt 7 - \sqrt 5 } \right).\left( {\sqrt 7 - \sqrt 5 } \right)$

$= - \left( {\sqrt 7 + \sqrt 5 } \right)\left( {\sqrt 7 - \sqrt 5 } \right)$

$= - \left( {7 - 5} \right) = - 2$

Câu 24 :

Cho biểu thức $P = \dfrac{x}{{\sqrt x + 1}}$. Giá trị của $P$ khi $x = \dfrac{2}{{2 - \sqrt 3 }}$ là

A.

$4$
B.

$2$
C.

$3$
D.

$1$

Đáp án : B

Phương pháp giải :

-Sử dụng các phép biến đổi như trục căn thức ở mẫu và đưa về hằng đẳng thức để rút gọn biến số trước khi thay vào biểu thức

-Thay giá trị của biến (thỏa mãn điều kiện) vào biểu thức và thực hiện phép tính

Lời giải chi tiết :

Ta có $x = \dfrac{2}{{2 - \sqrt 3 }} = \dfrac{{2\left( {2 + \sqrt 3 } \right)}}{{\left( {2 - \sqrt 3 } \right)\left( {2 + \sqrt 3 } \right)}} = \dfrac{{4 + 2\sqrt 3 }}{{4 - 3}} = 4 + 2\sqrt 3 = {\left( {\sqrt 3 + 1} \right)^2}$.$ \Rightarrow \sqrt x = \sqrt {{{\left( {\sqrt 3 + 1} \right)}^2}} = \sqrt 3 + 1$

Khi đó ta có $P = \dfrac{{4 + 2\sqrt 3 }}{{\sqrt 3 + 1 + 1}} = \dfrac{{4 + 2\sqrt 3 }}{{\sqrt 3 + 2}} = \dfrac{{2\left( {\sqrt 3 + 2} \right)}}{{\sqrt 3 + 2}} = 2$.

Câu 25 :

A.

$m = \dfrac{1}{2}$
B.

$m = - \dfrac{1}{2}$
C.

$m = 2$
D.

$m = - 2$

Đáp án : A

Phương pháp giải :

Để $M\left( {{x_0};{y_0}} \right)$ là giao của hai đường thẳng ${d_1}$ và ${d_2}$ ta thay tọa độ điểm $M$ vào từng phương trình đường thẳng để tìm $m$.

Lời giải chi tiết :

Nhận thấy $M \in {d_2}$.

Ta thay tọa độ điểm $M$ vào phương trình ${d_1}$ được phương trình $3 = - \left( {2m - 2} \right).1 + 4m \Leftrightarrow m = \dfrac{1}{2}$

Vậy $m = \dfrac{1}{2}.$

Câu 26 :

Viết phương trình đường thẳng $d$ biết $d$ đi qua hai điểm $A\left( {3;3} \right);B\left( { - 1;4} \right)$

A.

$y = \dfrac{1}{4}x - \dfrac{{15}}{4}$
B.

$y = - \dfrac{1}{4}x + \dfrac{{15}}{4}$
C.

$y = - \dfrac{1}{4}x - \dfrac{{15}}{4}$
D.

$y = \dfrac{1}{4}x + \dfrac{{15}}{4}$

Đáp án : B

Phương pháp giải :

Bước 1: Gọi phương trình đường thẳng cần tìm là $y = ax + b\,\,$$\left( {a \ne 0} \right)$

Bước 2: Thay tọa độ hai điểm $A,B$ vào phương trình đường thẳng $d$ để tìm hệ số $a,b$.

Lời giải chi tiết :

Gọi phương trình đường thẳng cần tìm là $y = ax + b\,\,$$\left( {a \ne 0} \right)$

Thay tọa độ điểm $A$ vào phương trình đường thẳng $d$ ta được $3a + b = 3$$ \Rightarrow b = 3 - 3a$

Thay tọa độ điểm $B$ vào phương trình đường thẳng $d$ ta được $ - 1.a + b = 4$$ \Rightarrow b = 4 + a$

Suy ra $3 - 3a = 4 + a \Leftrightarrow 4a = - 1 \Leftrightarrow a = - \dfrac{1}{4}$$ \Rightarrow b = 4 + a = 4 + \left( { - \dfrac{1}{4}} \right) = \dfrac{{15}}{4} \Rightarrow y = \dfrac{{ - 1}}{4}x + \dfrac{{15}}{4}$.

Vậy $d:y = - \dfrac{1}{4}x + \dfrac{{15}}{4}$.

Câu 27 :

Viết phương trình đường thẳng $d$ biết $d$ tạo với trục $Ox$ một góc bằng $30^\circ $ và cắt trục hoành tại điểm có hoành độ bằng $6$.

A.

$y = \dfrac{{\sqrt 3 }}{3}x$
B.

$y = \dfrac{{\sqrt 3 }}{3}x + 2\sqrt 3 $
C.

$y = \dfrac{{\sqrt 3 }}{3}x - 2\sqrt 3 $
D.

$y = \sqrt 3 x - 2\sqrt 3 $

Đáp án : C

Phương pháp giải :

Gọi phương trình đường thẳng $d:y = ax + b$$\left( {a \ne 0} \right)$

Xác định hệ số $a$ dựa vào góc tạo bởi đường thẳng với trục $Ox$, tìm $b$ dựa vào điểm đi qua

Lời giải chi tiết :

Gọi phương trình đường thẳng $d:y = ax + b$ $\left( {a \ne 0} \right)$

Vì góc tạo bởi đường thẳng $d$ và trục $Ox$ là $30^\circ $ nên $a = \tan 30^\circ = \dfrac{{\sqrt 3 }}{3}$

$ \Rightarrow y = \dfrac{{\sqrt 3 }}{3}x + b$

Vì đường thẳng $d$ cắt trục hoành tại điểm có hoành độ $6$ nên $d$ giao với trục hoành tại $A\left( {6;0} \right)$.

Thay tọa độ điểm $A$ vào phương trình đường thẳng $d$ ta được $\dfrac{{\sqrt 3 }}{3}.6 + b = 0 \Rightarrow b = - 2\sqrt 3 $

Nên $d:y = \dfrac{{\sqrt 3 }}{3}x - 2\sqrt 3 $.

Câu 28 :

Tính $x,y$ trong hình vẽ sau:

A.

$x = 2\sqrt 5 ;y = \sqrt 5 $
B.

$x = \sqrt 5 ;y = 3\sqrt 5 $
C.

$x = \sqrt 5 ;y = 2\sqrt 5 $
D.

$x = 2\sqrt 5 ;y = 2\sqrt 5 $

Đáp án : C

Phương pháp giải :

Bước 1: Tính $AH$ theo hệ thức $A{H^2} = BH.CH$

Bước 2: Tính $x;y$ theo định lý Pytago

Lời giải chi tiết :

Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:

$A{H^2} = BH.CH$$ \Rightarrow A{H^2} = 1.4 \Rightarrow AH = 2$

Áp dụng định lý Pytago cho tam giác vuông $AHB;AHC$ ta có

$AB = \sqrt {A{H^2} + H{B^2}} = \sqrt 5 ;AC = \sqrt {A{H^2} + H{C^2}} = 2\sqrt 5 $

Vậy $x = \sqrt 5 ;y = 2\sqrt 5 $.

Câu 29 :

Chọn kết luận đúng về giá trị biểu thức $B = \dfrac{{{{\cos }^2}\alpha - 3{{\sin }^2}\alpha }}{{3 - {{\sin }^2}\alpha }}$ biết $\tan \alpha = 3.$

A.

$B > 0$
B.

$B < 0$
C.

$0 < B < 1$
D.

$B = 1$

Đáp án : B

Phương pháp giải :

Chia cả tử và mẫu cho ${\cos ^2}\alpha $ rồi sử dung công thức $\tan \alpha = \dfrac{{\sin \alpha }}{{\cos \alpha }};\,1 + {\tan ^2}\alpha = \dfrac{1}{{{{\cos }^2}\alpha }}$ đề biến đổi và tính toán

Lời giải chi tiết :

Vì $\tan \alpha = 3 \ne 0 \Rightarrow \cos \alpha \ne 0.$ Chia cả tử và mẫu của $B$ cho ${\cos ^2}\alpha $ ta được

$B = \dfrac{{\dfrac{{{{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} - 3\dfrac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }}}}{{\dfrac{3}{{{{\cos }^2}\alpha }} - \dfrac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }}}} = \dfrac{{1 - 3{{\tan }^2}\alpha }}{{3.\dfrac{1}{{{{\cos }^2}\alpha }} - {{\tan }^2}\alpha }}$

$ = \dfrac{{1 - 3{{\tan }^2}\alpha }}{{3\left( {1 + {{\tan }^2}\alpha } \right) - {{\tan }^2}\alpha }} = \dfrac{{1 - 3{{\tan }^2}\alpha }}{{3 + 2{{\tan }^2}\alpha }}$

$ = \dfrac{{1 - 3.9}}{{3 + 2.9}} = - \dfrac{{26}}{{21}}$

Hay $B = - \dfrac{{26}}{{21}} < 0$

Câu 30 :

A.

$2,61\,m$
B.

$2,81\,m$
C.

$2,58\,m$
D.

$2,56\,m$

Đáp án : D

Lời giải chi tiết :

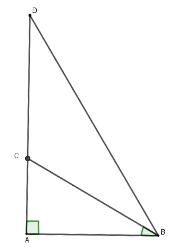
Từ giả thiết ta có chiều dài ban đầu của cây là $AD$; sau khi bị sét đánh thì cây còn lại $AC = 1\,\,m;\widehat {CBA} = 40^\circ $và $CD = CB$.

Xét tam giác $\Delta ABC$ vuông tại $A$ có $BC = \dfrac{{AC}}{{\sin 40^\circ }} = 1,56\,m$ nên $CD=1,56\,m$

Suy ra $AD = AC + CD $

$= 1 + 1,56 = 2,56\,m$.

Vậy cây cao $2,56\,m$.

Câu 31 :

Cho hình vuông $ABCD$. Gọi $M,N$ lần lượt là trung điểm của $AB,BC$ . Gọi $E$ là giao điểm của $CM$ và $DN$. Tâm của đường tròn đi qua bốn điểm $A,D,E,M$ là

A.

Trung điểm của $DM$.
B.

Trung điểm của $DB$.
C.

Trung điểm của $DE$.
D.

Trung điểm của $DA$.

Đáp án : A

Phương pháp giải :

Bước 1: Đưa các điểm đã cho về các đỉnh của tam giác vuông.

Bước 2: Tìm điểm cách đều cả bốn đỉnh $A,D,E,M$. Điểm đó chính là tâm của đường tròn.

Lời giải chi tiết :

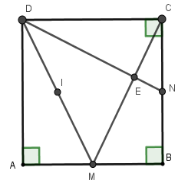
+) Ta có $\Delta DCN = \Delta CMB\left( {c - g - c} \right) $

$\Rightarrow\widehat {CDN} = \widehat {ECN}$ nên $\widehat {CNE} + \widehat {ECN} = \widehat {CNE} + \widehat {CDN} = 90^\circ $ suy ra $\widehat {CEN} = 90^\circ \Rightarrow CM \bot DN$

+) Gọi $I$ là trung điểm của $DM$.

Xét tam giác vuông $ADM$ ta có $AI = ID = IM = \dfrac{{DM}}{2}$. Xét tam giác vuông $DEM$ ta có $EI = ID = IM = \dfrac{{DM}}{2}$

Nên $EI = ID = IM = IA = \dfrac{{DM}}{2}$

Do đó bốn điểm $A,D,E,M$ cùng thuộc đường tròn tâm $I$ bán kính $\dfrac{{DM}}{2}$.

Câu 32 :

Cho đường tròn $\left( {O;R} \right)$ có hai dây $AB,CD$ vuông góc với nhau ở $M$. Biết$\,CD = 8\,cm;\,MC = 1\,cm$. Khoảng cách từ tâm $O$ đến dây $AB$ là

A.

$4\,cm$
B.

$5\,cm$
C.

$3\,cm$
D.

$2\,cm$

Đáp án : C

Phương pháp giải :

Kẻ các đường vuông góc từ tâm đến dây.

Sử dụng mối liên hệ giữa dây và đường kính và tính chất hình chữ nhật để suy ra khoảng cách.

Lời giải chi tiết :

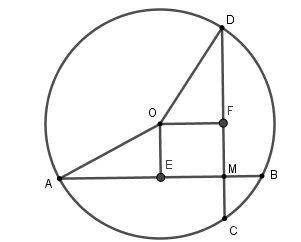
Xét đường tròn tâm $\left( O \right)$,

Kẻ $OE \bot AB$ tại $E$ suy ra $E$ là trung điểm của $AB$, kẻ $OF \bot CD$ tại $F$ suy ra $F$ là trung điểm của $CD$,

Xét tứ giác $OEMF$ có $\widehat E = \widehat F = \widehat M = 90^\circ $ nên $OEIF$ là hình chữ nhật, suy ra $FM = OE$.

Ta có $CD = 8\,cm \Rightarrow FC = 4\,cm$ mà $MC = 1\,cm \Rightarrow FM = FC - MC = 4 - 1 = 3\,cm$ nên $OE = FM = \,3cm$

Vậy khoảng cách từ tâm $O$ đến dây $AB$ là $3\,cm$

Câu 33 :

Cho tam giác $ABC$ cân tại $A$; đường cao $AH$ và $BK$ cắt nhau tại $I$. Khi đó đường thẳng nào sau đây là tiếp tuyến của đường tròn đường kính $AI$.

A.

$HK$
B.

$IB$
C.

$IC$
D.

$AC$

Đáp án : A

Phương pháp giải :

Sử dụng cách chứng minh tiếp tuyến

Để chứng minh đường thẳng $d$ là tiếp tuyến của đường tròn $\left( {O;R} \right)$ tại tiếp điểm là $M$ ta chứng minh $OM \bot d$ tại $M$ và $M \in \left( O \right)$.

Lời giải chi tiết :

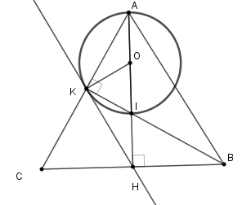
Gọi $O$ là trung điểm $AI$. Xét tam giác vuông $AIK$ có $OK = OI = OA \Rightarrow K \in \left( {O;\dfrac{{AI}}{2}} \right)$ (*)

Ta đi chứng minh $OK \bot KH$ tại $K$.

Xét tam giác $OKA$ cân tại $O$ ta có $\widehat {OKA} = \widehat {OAK}$ $\left( 1 \right)$

Vì tam giác $ABC$ cân tại $A$ có đường cao $AH$ nên $H$ là trung điểm của$BC$ . Xét tam giác vuông $BKC$ có $HK = HB = HC = \dfrac{{BC}}{2}$

Suy ra tam giác $KHB$ cân tại $H$ nên $\widehat {HKB} = \widehat {HBK}$$\left( 2 \right)$

Mà $\widehat {HBK} = \widehat {KAH}$ (cùng phụ với $\widehat {ACB}$) $\left( 3 \right)$

Từ $\left( 1 \right);\left( 2 \right);\left( 3 \right)$ suy ra $\widehat {HKB} = \widehat {AKO}$ mà $\widehat {AKO} + \widehat {OKI} = 90^\circ \Rightarrow \widehat {HKB} + \widehat {OKI} = 90^\circ \Rightarrow \widehat {OKH} = 90^\circ $ hay $OK \bot KH$ tại $K$ (**)

Từ (*) và (**) thì $HK$ là tiếp tuyến của đường tròn đường kính $AI$.

Câu 34 :

Trên mặt phẳng tọa độ $Oxy$, cho điểm $A\left( {4;5} \right)$. Hãy xác định vị trí tương đối của đường tròn $\left( {A;5} \right)$ và các trục tọa độ.

A.

Trục tung cắt đường tròn và trục hoành tiếp xúc với đường tròn.
B.

Trục hoành cắt đường tròn và trục tung tiếp xúc với đường tròn
C.

Cả hai trục tọa độ đều cắt đường tròn
D.

Cả hai trục tọa độ đều tiếp xúc với đường tròn.

Đáp án : A

Phương pháp giải :

Bước 1: Xác định khoảng cách từ tâm $A$ đến các trục tọa độ.

Bước 2: Sử dụng vị trí tương đối giữa đường thẳng và đường tròn.

Lời giải chi tiết :

Vì $A\left( {4;5} \right)$ nên khoảng cách từ $A$ đến trục hoành là ${d_1} = \left| {{y_A}} \right| = 5$, khoảng cách từ $A$ đến trục tung là ${d_2} = \left| {{x_A}} \right| = 4$

Nhận thấy ${d_2} = R\left( { = 5} \right)$ nên trục hoành tiếp xúc với đường tròn $\left( {A;5} \right)$.

Và ${d_2} = 4 < 5 = R$ nên trục tung cắt đường tròn $\left( {A;5} \right)$.

Câu 35 :

A.

$8\,cm$
B.

$\,8\sqrt 3\,cm$
C.

$\dfrac {8}{\sqrt 3}\,cm$
D.

$5\,cm$

Đáp án : C

Phương pháp giải :

Sử dụng tính chất hai tiếp tuyến cắt nhau và công thức chu vi tam giác

Sử dụng tỉ số lượng giác của góc nhọn

Lời giải chi tiết :

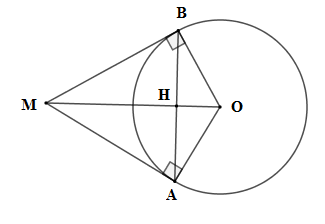
Xét $\left( O \right)$ có $MA = MB$ (tính chất hai tiếp tuyến cắt nhau) mà $\widehat {AMB} = 60^\circ $ nên $\Delta MAB$ đều suy ra chu vi $\Delta MAB$ là $MA + MB + AB = 3AB = 24 $$\Rightarrow AB = 8cm = MA = MB$

Lại có $\widehat {AMO} = \dfrac{1}{2}\widehat {AMB} = 30^\circ $ (tính chất 2 tiếp tuyến cắt nhau)

Xét tam giác vuông $MAO$ có $\tan \widehat {AMO} = \dfrac{{OA}}{{MA}} \Rightarrow OA = MA.\tan 30^\circ = \dfrac {8}{\sqrt 3}\,cm$

Câu 36 :

A.

$\dfrac{{27}}{6}$ ( đvdt)
B.

$27$( đvdt)
C.

$\dfrac{{27}}{2}$ (đvdt)
D.

$\dfrac{{27}}{4}$(đvdt)

Đáp án : D

Phương pháp giải :

- Xác định giao điểm 2 đường thẳng đã cho

- Dựng đường cao của tam giác được tạo thành

- Tính độ dài các đoạn thẳng

- Tính diện tích tam giác.

Lời giải chi tiết :

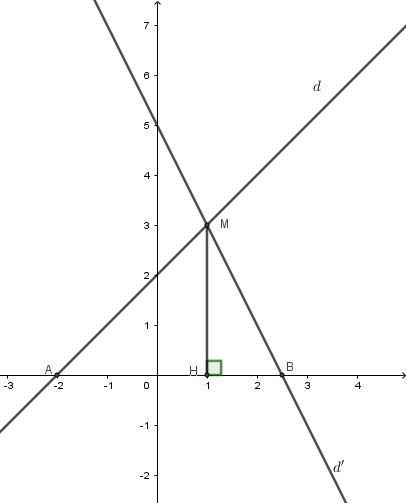
Xét phương trình hoành độ giao điểm của ${d_1};{d_2}$

$x + 2 = - 2x + 5 \Leftrightarrow x = 1 \Rightarrow y = 3 \Rightarrow {d_1} \cap {d_2}$ tại $ M(1;3)$

Gọi $H$ là chân đường vuông góc kẻ từ $M$ tới $Ox$. Suy ra $MH = 3$

$d \cap Ox$ tại $ A( - 2;0) \Rightarrow OA = 2$

$d' \cap Ox$ tại $ B\left( {\dfrac{5}{2};0} \right) \Rightarrow OB = \dfrac{5}{2}$

$\Rightarrow AB = OA+OB=2 + \dfrac{5}{2} = \dfrac{9}{2}$

${S_{MAB}} = \dfrac{1}{2}AB.MH = \dfrac{1}{2}.\dfrac{9}{2}.3 = \dfrac{{27}}{4}\,(dvdt)$

Câu 37 :

Cho tam giác nhọn $ABC$ hai đường cao $AD$ và $BE$ cắt nhau tại $H$. Biết $HD:HA = 1:2$. Tính $\tan B.\tan C$

A.

$\dfrac{1}{2}$
B.

$\dfrac{1}{3}$
C.

$2$
D.

$3$

Đáp án : D

Phương pháp giải :

+ Sử dụng định nghĩa tỉ số lượng giác của góc nhọn

+ Tam giác đồng dạng

+ Tính chất dãy tỉ số bằng nhau

Lời giải chi tiết :

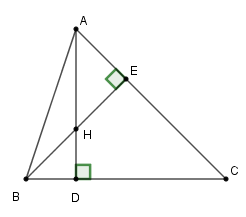
Ta có: $\tan B = \dfrac{{AD}}{{BD}};\tan C = \dfrac{{AD}}{{CD}}$.

Suy ra $\tan B.\tan C = \dfrac{{A{D^2}}}{{BD.CD}}$ (1)

$\widehat {HBD} = \widehat {CAD}$ (cùng phụ với $\widehat {ACB}$); $\widehat {HDB} = \widehat {ADC} = {90^0}$.

Do đó $\Delta BDH \backsim \Delta ADC$ (g.g), suy ra $\dfrac{{DH}}{{DC}} = \dfrac{{BD}}{{AD}}$, do đó $BD.DC = DH.AD$ (2).

Từ (1) và (2) suy ra $\tan B.\tan C = \dfrac{{A{D^2}}}{{DH.AD}} = \dfrac{{AD}}{{DH}}$ (3).

Theo giả thiết $\dfrac{{HD}}{{AH}} = \dfrac{1}{2}$ suy ra $\dfrac{{HD}}{{AH + HD}} = \dfrac{1}{{2 + 1}}$ hay $\dfrac{{HD}}{{AD}} = \dfrac{1}{3}$, suy ra $AD = 3HD$.

Thay vào (3) ta được: $\tan B.\tan C = \dfrac{{3HD}}{{DH}} = 3$.