Tuần 12: Nhân một số thập phân với 10, 100, 1000, ... Nhân một số thập phân với một số thập phân trang 41
Tính: 8,12 x 10 = ……… 6,44 x 100 = ………. 9,89 x 1000 = ………. 54,78 x 10 = ……… 0,567 x 100 = ……… 7,06 x 1000 = ………. Viết số thích hơp vào chỗ chấm: 15,2m = ……….dm 0,745m = ………..cm 3,28dm = ……….cm 37cm = ………..m 376cm = …….……m 71cm = …….…….dm
Bài 1
Tính:
8,12 x 10 = ……… 6,44 x 100 = ………. 9,89 x 1000 = ……….
54,78 x 10 = ……… 0,567 x 100 = ……… 7,06 x 1000 = ……….
Phương pháp giải:
Muốn nhân một số thập phân với 10,100,1000,... ta chỉ việc chuyển dấu phẩy của số đó lần lượt sang bên phải một, hai, ba,… chữ số.
Lời giải chi tiết:
8,12 x 10 =81,2 6,44 x 100 = 644 9,89 x 1000 = 9890
54,78 x 10 = 547,8 0,567 x 100 = 56,7 7,06 x 1000 = 7060
Bài 2
Viết số thích hơp vào chỗ chấm:
15,2m = ……….dm 0,745m = ………..cm 3,28dm = ……….cm
37cm = ………..m 376cm = …….……m 71cm = …….…….dm
Phương pháp giải:
Áp dụng cách đổi:
1m = 10dm 1m = 100 cm 1dm = 10cm
Lời giải chi tiết:
15,2m = 152dm 0,745m = 74,5cm 3,28dm = 32,8cm
37cm = 0,37m 376cm = 3,76m 71cm = 7,1dm
Câu 3
Đặt tính rồi tính.
a) 37,2 x 70 b) 28,6 x 500 c) 0,54 x 3000
………………….. …………………... ………………………
…………………. ………………….. ………………………
…………………. ………………….. ………………………
Phương pháp giải:
Đặt tính theo cột dọc, rồi nhân như phép nhân các số tự nhiên.
Lời giải chi tiết:
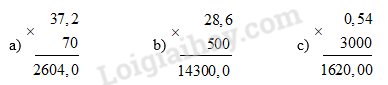
Bài 4
Một chiếc can chứa 5 lít nước mắm. Biết một lít nước mắm cân nặng 1,04kg và chiếc can rỗng nặng 1,2kg. Hỏi can nước mắm đó cân nặng bao nhiêu ki-lô-gam?
Phương pháp giải:
- Cân nặng của 5 lít nước mắm bằng cân nặng của 1 lít nước mắm nhân với 5.
- Cân nặng của can nước mắm = Cân nặng của 5 lít nước mắm + Cân nặng của chiếc can rỗng.
Lời giải chi tiết:
Cân nặng của 5 lít nước mắm là
1,04 x 5 = 5,2 (kg)
Cân nặng của can nước mắm đó là
5,2 + 1,2 = 6,4 (kg)
Đáp số: 6,4 kg
Bài 5
Đặt tính rồi tính:
17,4 x 3,6 0,58 x 6,7 3,725 x 2,4
…………………. …………………. ……………………
…………………. …………………. ……………………
…………………. …………………. ……………………
Phương pháp giải:
Đặt tính theo cột dọc, rồi nhân như phép nhân các số tự nhiên.
Lời giải chi tiết:
Bài 6
Tính nhẩm:
7,4 x 0,001 = ………… 3,7 x 0,001 = ……….. 4,85 x 0,1 = ………….
8,32 x 0,01 = ………… 300 x 0,01 = ……….. 1,78 x 0,01 = …………
Phương pháp giải:
Khi nhân một số thập phân với 0,1; 0,01; 0,001;... ta chỉ việc chuyển dấu phẩy của số đó lần lượt sang bên trái một, hai, ba, … chữ số.
Lời giải chi tiết:
7,4 x 0,001 = 0,0074 3,7 x 0,001 = 0,0037 4,85 x 0,1 = 0,485
8,32 x 0,01 = 0,0832 300 x 0,01 = 3,00 1,78 x 0,01 = 0,0178
Bài 7
Tính bằng cách thuận tiện.
a) 1,25 x 0,36 x 0,08 = ……………………………………………………………………
b) 73,5 – 8,76 – 15,24 = ………………………………………………………………….
c) 37 – 5,28 + 3,28 = ……………………………………………………………………..
d) 8,27 x 0,02 – 3,35 x 0,01 = ……………………………………………………………
Phương pháp giải:
- Nhóm các số thành 1 tổng hoặc tích có kết quả là số tròn chục, tròn trăm, …
- Áp dụng công thức nhân một số với một hiệu: a × (b − c) = a × b – a × c
Lời giải chi tiết:
a) 1,25 x 0,36 x 0,08 = (1,25 x 0,08) x 0,36
= 0,1 x 0,36 = 0,036
b) 73,5 – 8,76 – 15,24 = 73,5 – (8,76 + 15,24)
= 73,5 – 24 = 49,5
c) 37 – 5,28 + 3,28 = 37 – (5,28 – 3,28) = 37 – 2 = 35
d) 8,27 x 0,02 – 3,35 x 0,01 = 8,27 x 2 x 0,01 – 3,35 x 0,01
= 16,54 x 0,01 – 3,35 x 0,01
= 0,01 x (16,54 – 3,35)
= 0,01 x 13,19
= 0,1319
Bài 8
Một xe ô tô đi trong 4 giờ được 224km. Trong hai giờ đầu tiên, trung bình mỗi giờ ô tô đó đi được 58,75km, giờ thứ ba, ô tô đó đi được ít hơn trung bình mỗi giờ đầu tiên 2,5km. Hỏi giờ thứ tư ô tô đó đi được bao nhiêu ki-lô-mét?
Phương pháp giải:
- Quãng đường đi được trong 2 giờ đầu tiên = Quãng đường trung bình đi trong hai giờ đầu nhân với 2.
- Quãng đường đi được trong giờ thứ ba = Quãng đường trung bình mỗi giờ đầu tiên – 2,5 km
- Quãng đường đi được trong giờ thứ tư = Tổng quãng đường đi trong 4 giờ - Quãng đường đi trong 3 giờ đầu.
Lời giải chi tiết:
Tóm tắt
4 giờ: 224km
2 giờ đầu: trung bình mỗi giờ 58,75km
Giờ thứ ba: ít hơn trung bình mỗi giờ đầu 2,5km
Giờ thứ tư: ….km?
Bài giải
Trong 2 giờ đầu tiên ô tô đi được số ki-lô-mét là
58,75 x 2 = 117,5 (km)
Giờ thứ ba ô tô đó đi được quãng đường là
58,75 – 2,5 = 56,25 (km)
Giờ thứ tư ô tô đó đi được số ki-lô-mét là
224 – ( 117,5 + 56,25) = 50,25 (km)
Đáp số: 50,25km
Vui học
Một mảnh vườn có hình dạng và kích thước như hình vẽ. Tính chu vi và diện tích mảnh vườn?

Phương pháp giải:
Chia mảnh vườn thành hai hình rồi tính tổng chu vi và diện tích hai hình đó.
Lời giải chi tiết:
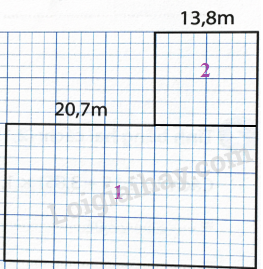
Chia mảnh đất thành hai hình 1 và hình 2.
Chiều dài hình thứ nhất là
20,7 + 13,8 = 34,5 (m)
Chu vi mảnh vườn là
20,7 + 20,7 + 34,5 + 34,5 + 13,8 + 13,8 = 138 (m)
Diện tích hình chữ nhật số 1 là
34,5 x 20,7 = 714,15 (m2)
Diện tích hình vuông số 2 là
13,8 x 13,8 = 190,44 (m2)
Diện tích mảnh vườn là
714,15 + 190,44 = 904,59 (m2)
Đáp số: Chu vi: 138 m
Diện tích: 904,59 m2
- Tuần 13: Luyện tập chung. Chia một số thập phân cho một số tự nhiên. Chia một số thập phân cho 10, 100, 1000,... trang 44
- Tuần 14: Chia một số tự nhiên cho một số tự nhiên mà thương tìm được là một số thập phân. Chia một số tự nhiên, một số thập phân cho một số thập phân trang 47
- Tuần 15: Luyện tập chung. Tỉ số phần trăm. Giải toán về tỉ số phần trăm trang 51
- Tuần 16: Giải toán về tỉ số phần trăm (tiếp theo)
- Tuần 17: Luyện tập chung. Sử dụng máy tính bỏ túi để giải toán về tỉ số phần trăm. Hình tam giác trang 57
>> Xem thêm
Các bài khác cùng chuyên mục
- Kiểm tra cuối học kì 1 trang 65
- Tuần 18: Diện tích hình tam giác trang 61
- Tuần 17: Luyện tập chung. Sử dụng máy tính bỏ túi để giải toán về tỉ số phần trăm. Hình tam giác trang 57
- Tuần 16: Giải toán về tỉ số phần trăm (tiếp theo)
- Tuần 15: Luyện tập chung. Tỉ số phần trăm. Giải toán về tỉ số phần trăm trang 51
- Kiểm tra cuối học kì 1 trang 65
- Tuần 18: Diện tích hình tam giác trang 61
- Tuần 17: Luyện tập chung. Sử dụng máy tính bỏ túi để giải toán về tỉ số phần trăm. Hình tam giác trang 57
- Tuần 16: Giải toán về tỉ số phần trăm (tiếp theo)
- Tuần 15: Luyện tập chung. Tỉ số phần trăm. Giải toán về tỉ số phần trăm trang 51





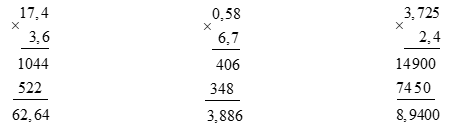








Danh sách bình luận