Tuần 33: Ôn tập về tính diện tích, thể tích một số hình. Một số dạng bài toán đã học - trang 55

Bài 1

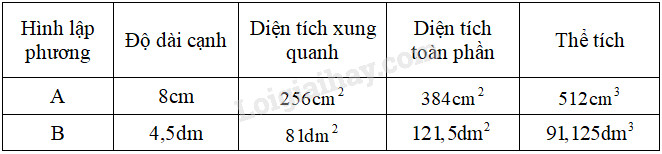
Viết số đo thích hợp vào ô trống: 

Phương pháp giải:

Áp dụng các quy tắc :

- Tính diện tích một mặt ta lấy cạnh nhân với cạnh.

- Muốn tính diện tích xung quanh của hình lập phương ta lấy diện tích một mặt nhân với \(4\).

- Muốn tính diện tích toàn phần của hình lập phương ta lấy diện tích một mặt nhân với \(6\).

- Muốn tính thể tích hình lập phương ta lấy cạnh nhân với cạnh rồi nhân với cạnh.

Lời giải chi tiết:

a) Hình lập phương A:

Diện tích một mặt của hình lập phương đó là:

             \(8 \times 8 = 64\,\,(c{m^2})\) 

Diện tích xung quanh của hình lập phương đó là:

             \(64 \times 4 = 256\,\,(c{m^2})\)

Diện tích toàn phần của hình lập phương đó là:

              \(64 \times 6 = 384\,\,(c{m^2})\)

Thể tích hình lập phương đó là:

              \(8 \times 8 \times 8 = 512\,\,(c{m^3})\)

b) Hình lập phương B:

Diện tích một mặt của hình lập phương đó là:

            \(4,5 \times 4,5 = 20,25\,\,(d{m^2})\) 

Diện tích xung quanh của hình lập phương đó là:

            \(20,25 \times 4 = 81\,\,(d{m^2})\)

Diện tích toàn phần của hình lập phương đó là:

            \(20,25 \times 6 = 121,5\,\,(d{m^2})\)

Thể tích hình lập phương đó là:

         \(4,5 \times 4,5 \times 4,5 = 91,125\,\,(d{m^3})\)

Ta có bảng kết quả như sau: 

Bài 2

Một bể nước dạng hình hộp chữ nhật có chiều rộng 1,2m (tính cả thành bể) và bằng \(\dfrac{2}{3}\) chiều dài. Chiều cao bằng \(\dfrac{5}{6}\) chiều dài (tính cả bề dày đáy bể). Tính thể tích của bể nước đó.

Phương pháp giải:

- Tính chiều dài của bể ta lấy chiều rộng của bể chia cho \(\dfrac{2}{3}\) hoặc lấy chiều rộng chia cho 2 rồi nhân với 3.

- Tính chiều cao của bể ta lấy chiều dài nhân với \(\dfrac{5}{6}\) hoặc lấy chiều dài cho cho 6 rồi nhân với 5.

- Tính thể tích của bể ta lấy chiều dài nhân với chiều rộng  rồi nhân với chiều cao.

Lời giải chi tiết:

Chiều dài của bể nước đó là:

          \(1,2:2 \times 3 = 1,8\,\,(m)\,\)

Chiều cao của bể nước đó là:

          \(1,8:6 \times 5 = 1,5\,\,(m)\)

Thể tích của bể nước đó là:

          \(1,8 \times 1,2 \times 1,5 = 3,24\,\,({m^3})\)

                              Đáp số: \(3,24{m^3}\).

Bài 3

Người ta đóng một thùng gỗ đựng thóc hình hộp chữ nhật có chiều dài 1,8m; chiều rộng 1,2m; chiều cao 0,8m.

a) Tính diện tích gỗ để đóng chiếc thùng đó.

b) Tính tiền mua gỗ, biết 1m² có giá 650 000 đồng.

Phương pháp giải:

Do chiếc thùng dùng để đựng thóc nên chiếc thùng đó có nắp. Do đó, diện tích gỗ để đóng chiếc thùng đó bằng diện tích toàn phần của chiếc thùng.

Để giải bài này ta có thể làm như sau:

- Tính diện tích xung quanh ta lấy chu vi đáy nhân với chiều cao.

- Tính diện tích một đáy ta lấy chiều dài nhân với chiều rộng.

- Tính diện tích toàn phần ta lấy diện tích xung quanh cộng với diện tích hai đáy.

- Tính số tiền để mua gỗ ta lấy giá tiền để mua \(1{m^2}\) gỗ nhân với diện tích gỗ dùng để đóng chiếc thùng đó.

Lời giải chi tiết:

a) Do chiếc thùng dùng để đựng thóc nên chiếc thùng đó có nắp. Do đó, diện tích gỗ để đóng chiếc thùng đó bằng diện tích toàn phần của chiếc thùng.

Diện tích xung quanh của chiếc thùng đó là:

      \((1,8 + 1,2) \times 2 \times 0,8 = 4,8\,\,({m^2})\)

Diện tích đáy của chiếc thùng đó là:

      \(1,8 \times 1,2 = 2,16\,\,({m^2})\)

Diện tích gỗ để đóng chiếc thùng đó là:

      \(4,8 + 2,16 \times 2 = 9,12\,\,({m^2})\)

b) Số tiền mua gỗ để đóng chiếc thùng đó là:

      \(650\,\,000 \times 9,12 = 5\,\,928\,\,000\) (đồng)

                    Đáp số : a) \(9,12m^2\) ;

                                   b) \(5\,\,928\,\,000\) đồng.

Bài 4

Nếu thành bể và đáy bể ở bài 2 dày 10cm thì bể có thể chứa được bao nhiêu lít nước? (1dm³ = 1 lít)

Phương pháp giải:

- Đổi \(10cm{\rm{ }} = {\rm{ }}0,1m\).

- Tính độ dài của thành bể ở cả hai bên của bể ta lấy \(0,1m\) nhân với \(2\).

- Tính chiều dài, chiều rộng của lòng bể ta lần lượt lấy chiều dài, chiều rộng của bể trừ đi \(0,2m\).

- Tính chiều cao của lòng bể ta lấy chiều cao của bể trừ đi độ dài đáy bể.

- Tính thể tích của lòng bể ta lấy chiều dài của lòng bể nhân với chiều rộng của lòng bể rồi nhân với chiều cao của lòng bể (theo đơn vị đo là \({m^3}\)).

- Đổi diện tích từ đơn vị đo là \({m^3}\) sang đơn vị đo là \(d{m^3}\), từ đó tìm được số lít nước mà bể chứa được.

Lời giải chi tiết:

Đổi \(10cm{\rm{ }} = {\rm{ }}0,1m\).

Độ dài của thành bể ở cả hai bên của bể là:

           \(0,1 \times 2 = 0,2\,\,(m)\)

Chiều dài của lòng bể là:

           \(1,8 - 0,2 = 1,6\,\,(m)\)

Chiều rộng của lòng bể là:

          \(1,2 - 0,2 = 1\,\,(m)\)

Chiều cao của lòng bể là:

           \(1,5 - 0,1 = 1,4\,\,(m)\)

Bể đó có thể chứa số lít nước là:

          \(1,6 \times 1 \times 1,4 = 2,24\,\,({m^3})\)

          \(2,24{m^3} = 2240d{m^3} = 2240\) lít

                             Đáp số: \(2240\) lít nước. 

Loigiaihay.com

Bài 5

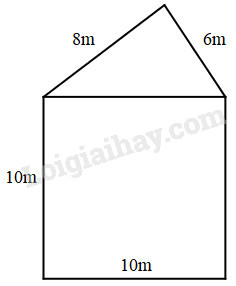
Người ta trồng hoa trên mảnh vườn như hình vẽ. Hằng năm, mỗi mét vuông thu được 120 000 đồng tiền bán hoa. Hỏi mỗi năm người ta thu được bao nhiêu tiền?

Phương pháp giải:

Quan sát hình vẽ ta thấy mảnh vườn đã cho gồm mảnh vườn hình vuông có cạnh dài 10m và mảnh vườn hình tam giác vuông có độ dài hai cạnh góc vuông là 8m và 6m.

Để giải bài này ta có thể làm như sau:

- Tính diện tích mảnh vườn hình vuông ta lấy cạnh nhân với cạnh.

- Tính diện tích mảnh vườn hình tam giác vuông ta lấy tích độ dài hai cạnh góc vuông chia cho 2.

- Tính diện tích mảnh vườn  ta lấy diện tích mảnh vườn hình vuông cộng với diện tích mảnh vườn tam giác vuông.

- Tính số tiền thu được ta lấy số tiền thu được trên mỗi mét vuông nhân với diện tích mảnh vườn.

Lời giải chi tiết:

Quan sát hình vẽ ta thấy mảnh vườn đã cho gồm mảnh vườn hình vuông có cạnh dài 10m và mảnh vườn hình tam giác vuông có độ dài hai cạnh góc vuông là 8m và 6m.

Diện tích mảnh vườn hình vuông là:

             \(10 \times 10 = 100\,\,({m^2})\)

Diện tích mảnh vườn hình tam giác vuông là:

             \(8 \times 6:2 = 24\,\,({m^2})\)

Diện tích mảnh vườn đó là:

             \(100 + 24 = 124\,\,({m^2})\)

Mỗi năm người ta thu được số tiền là:

             \(120\,\,000 \times 124 = 14\,\,880\,\,000\) (đồng)

                        Đáp số: \(14\,\,880\,\,000\) đồng.

Bài 6

Viết vào chỗ chấm cho thích hợp:

Có ba bao gạo, bao thứ nhất cân nặng 35kg, bao thứ hai cân nặng 45kg, bao thứ ba cân nặng 37kg. Trung bình mỗi bao gạo cân nặng ……..

Phương pháp giải:

Muốn tìm cân nặng trung bình của mỗi bao gạo ta lấy cân nặng của ba bao gạo chia cho 3.

Lời giải chi tiết:

Trung bình mỗi bao gạo nặng số ki-lô-gam là:

          \((35 + 45 + 37) : 3 = 39\;(kg)\) 

                                 Đáp số: \(39kg.\)

Bài 7

Lớp 5B có 35 bạn, trong đó có 14 bạn có chiều cao dưới 1,4m, còn lại là cao từ 1,4m trở lên. Tính tỉ số phần trăm số bạn cao từ 1,4m trở lên so với số học sinh của lớp 5B.

Phương pháp giải:

- Tìm số bạn cao từ 1,4m trở lên ta lấy số bạn của cả lớp trừ đi số bạn có chiều cao dưới 1,4m:  35 – 14 = 21 bạn

- Muốn tìm tỉ số phần trăm của số bạn cao từ 1,4m trở lên so với số học sinh của lớp 5B ta sẽ tìm thương giữa số bạn cao từ 1,4m trở lên và số học sinh của lớp 5B, tức là tìm thương của phép chia 21 : 35,  sau đó nhân thương đó với 100 và viết thêm kí hiệu % vào bên phải tích tìm được.

Lời giải chi tiết:

Lớp 5B có số bạn cao trên 1,4m là:

              \(35 \,– 14 = 21\) (bạn)

Tỉ số phần trăm của số bạn cao từ 1,4m trở lên so với số học sinh của lớp 5B là:

              \(21 : 35 = 0,6 =  60\%\)

                                Đáp số: \(60\%.\)

Bài 8

Một ô tô đi \(100km\) tiêu thụ hết \(8,5l\) xăng. Hỏi ô tô đó đi \(180km\) tiêu thụ hết bao nhiêu lít xăng?

Phương pháp giải:

Đối với bài toán về quan hệ tỉ lệ ta có thể giải theo 2 cách:

* Cách 1 (Rút về đơn vị):

- Tính số lít xăng tiêu thụ khi đi 1km.

- Tính số lít xăng tiêu thụ khi đi 180km ta lấy số lít xăng tiêu thụ khi đi 1km nhân với 180.

* Cách 2 (dùng tỉ số):

- Tìm tỉ số giữa 180km và 100km.

- 180km gấp 100km bao nhiêu lần thì số dầu tiêu thụ khi đi 180km cũng gấp số dầu tiêu thụ khi đi 100km bấy nhiêu lần.

Lời giải chi tiết:

Cách 1 : (Phương pháp rút về đơn vị)

Ô tô đi 1km tiêu thụ hết số lít xăng là:

\(8,5 : 100 = 0,085\) (lít)

Ô tô đi 180km tiêu thụ hết số lít xăng là:

\(0,085 × 180 = 15,3\) (lít)

                 Đáp số: \(15,3\) lít.

Cách 2: (Phương pháp tìm tỉ số)

\(180km\) gấp \(100km\) số lần là :

\(180:100=1,8\) (lần)

Ô tô đi 180km tiêu thụ hết số lít xăng là:

\(8,5 × 1,8 = 15,3\) (lít)

                 Đáp số: \(15,3\) lít.

Vui học

Người ta quét vôi toàn bộ tường trong và trần nhà của một lớp học có chiều dài 6,5m; chiều rộng 4,8m; chiều cao 3,2m.

a) Tính diện tích cần quét vôi, biết diện tích các cửa đi và cửa số là 12,2m².

b) Cứ quét vôi mỗi mét vuông thì hết 11 000 đồng. Tính số tiền quét vôi lớp học đó.

Phương pháp giải:

Các phần cần quét vôi của lớp học là toàn bộ tường trong (trừ phần cửa đi và cửa số) và trần, tức là diện tích xung quanh (trừ phần cửa đi và cửa sổ) và diện tích một đáy.

Để giải bài này ta có thể thực hiện các bước như sau:

- Tính diện tích xung quanh của lớp học ta lấy chu vi đáy nhân với chiều cao.

- Tính diện tích trần của lớp học ta lấy chiều dài nhân với chiều rộng.

Các phần cần quét vôi của lớp học là toàn bộ tường trong (trừ phần cửa đi và cửa số) và trần, tức là diện tích xung quanh (trừ phần cửa đi và cửa sổ) và diện tích một đáy.

Để giải bài này ta có thể thực hiện các bước như sau:

- Tính diện tích xung quanh của lớp học ta lấy chu vi đáy nhân với chiều cao.

- Tính diện tích trần của lớp học ta lấy chiều dài nhân với chiều rộng.

- Tính diện tích cần quét vôi ta lấy tổng diện tích xung quanh của căn phòng và diện tích trần trừ đi diện tích cửa và cửa sổ.

- Tính số tiền quét vôi lớp học đó ta lấy số tiên khi quét vôi mỗi mét vuông nhân với diện tích cần quét vôi.

Lời giải chi tiết:

a) Diện tích xung quanh của lớp học đó là:

   \((6,5 + 4,8) \times 2 \times 3,2 = 72,32\,\,({m^2})\)

Diện tích trần của lớp học đó là:

   \(6,5 \times 4,8 = 31,2\,\,({m^2})\)

Diện tích cần quét vôi là:

   \(72,32 + 31,2 - 12,2 = 91,32\,\,({m^2})\)

b) Số tiền quét vôi lớp học đó là:

     \(11\,\,000 \times 91,32 = 1\,\,004\,\,520\) (đồng)

                    Đáp số: a) \(103,2{m^2}\) ;  

                                  b) \(1\,\,004\,\,520\) đồng.

Lưu ý khi giải:

- Một số quên không trừ diện tích các cửa, từ đó tìm ra diện tích cần quét vôi là \(103,52{m^2}\); hoăc tính diện tích cần quét vôi bằng diện tích toàn phần trừ đi diện tích các cửa đi và cửa sổ.

Loigiaihay.com